强化学习经典算法笔记(四)：时间差分算法Temporal Difference（Q-Learning算法）

强化学习经典算法笔记——时间差分算法之 Q-Learning

强化学习经典算法笔记(零)：贝尔曼方程的推导
强化学习经典算法笔记(一)：价值迭代算法Value Iteration
强化学习经典算法笔记(二)：策略迭代算法Policy Iteration
强化学习经典算法笔记(三)：蒙特卡罗方法Monte Calo Method

简介

  上一篇讲的是比较经典的model-free的算法——蒙特卡罗算法。这一篇讲另一个很经典的无模型算法——时间差分算法Temporal Difference。

  参考文献 https://blog.csdn.net/weixin_37895339/article/details/74937023

  时间差分算法（TD Algorithm）既有Monte Calo算法的优势，又有Dynamic Programming的优势。类似Monte Calo，TD算法可以直接从原始数据中学到策略，而不需要掌握环境的模型；而Monte Calo算法必须在一个episode结束后才能更新V值或Q值，如果一个episode持续很长时间，则Monte Calo算法效率不高。TD算法这一点上比较像DP算法，每个action都可以更新，效率大大提升。

  按照On-policy或Off-policy之分，TD算法有两个代表性例子：

• Off-policy： Q Learning
• On-policy： SARSA

  On-policy算法是指与环境进行交互的policy和实际更新迭代的policy是同一个policy的算法；Off-policy算法是指，与环境交互的policy和实际更新的policy不是同一个policy的算法。

  形象地说，我看着别人玩游戏，从别人玩游戏的经验中，我自己也学到了如何玩游戏，这就是Off-policy，别人玩游戏，就是与环境交互的policy，而我自己就是进行更新和学习的policy。如果我亲自玩游戏，在这个过程中，我的游戏水平提高了，就是On-policy算法，即交互和学习的policy是一个policy。

  TD算法基本思想就是用（前一个状态的价值和当前状态的价值之差）来更新前一个状态的V值或Q值，尽管当前状态的估计值也不准确，用一个不准确的值来更新另一个不准确的值，叫做自举（Bootstrapping）。
$$V(s)=V(s)+\alpha [r+\gamma V(s^{\prime })-V(s)]$$

Q-Learning算法

  Q-Learning算法的具体流程。下图来自Reinforcement Learning An Introduction

  上面说Q-Learning算法是Off-policy的算法，是因为Q-learning算法在计算下一状态的预期收益时使用了max操作，直接选择最优动作，而当前policy并不一定能选择到最优动作，因此这里生成样本的policy和学习时的policy不同，为off-policy算法。

编程实验

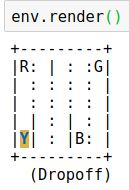
  这次选用的实验是Taxi-v2游戏，智能体在游戏中控制一辆出租车，游戏中有四个位置，出租车需要在一个位置接乘客，在另一个位置放下乘客，如果放下乘客的位置对了，得到+20分奖励，如果放错了，得-1分惩罚。如果接乘客和放乘客的操作都不合法，得-10分惩罚。
  R，G，Y，B代表不同位置和乘客，黄色方块代表出租车。

  直接贴出全部代码，太简单了就不解释了。

import random
import gym
import numpy as np
import matplotlib.pyplot as plt
import copy
%matplotlib inline

env = gym.make('Taxi-v2')

# 学习率
alpha = 0.4

# 折扣率
gamma = 0.999

# 贪心算法参数
epsilon = 0.017

# Q是表格函数，对简单的有限状态任务有效，如果是连续空间，或者复杂离散空间，都没法用查表的方法得到某个状态的Q值，应该用神经网络
q = {}

# 初始化所有(状态-动作)对的价值为0
for s in range(env.observation_space.n):
    for a in range(env.action_space.n):
        q[(s,a)] = 0

def update_q_table(prev_state, action, reward, nextstate, alpha, gamma):
    '''
    更新（State-Action）Pair的Q值
    '''
    # t+1 状态的Q值用 t+1 状态下得分最高的动作所对应的Q值
    qa = max([q[(nextstate, a)] for a in range(env.action_space.n)])
    
    # 一步时间差分
    q[(prev_state,action)] += alpha * (reward + gamma * qa - q[(prev_state,action)])

def epsilon_greedy_policy(state, epsilon):
    '''

    '''
    if random.uniform(0,1) < epsilon:
        # 在动作空间随机采样
        return env.action_space.sample()
    else:
        # 取当前状态下具有最高价值的动作
        return max(list(range(env.action_space.n)), key = lambda x: q[(state,x)])

# 记录每个episode获得的总回报
r_record = []
# 记录Q值表的新旧之差
error_qa = []
# 保存Q-Table更新前后的两个table，注意一定要用深度拷贝！！！
q_old = copy.deepcopy(q)

for i in range(2000):
    r = 0
    prev_state = env.reset()
    while True:

        #env.render()
     
        # 每一个状态都用epsilon-贪心算法计算应执行的动作
        action = epsilon_greedy_policy(prev_state, epsilon)
        
        # 执行动作，转移到下一状态，得到reward
        nextstate, reward, done, _ = env.step(action)
        
        # 更新Q值函数        
        update_q_table(prev_state, action, reward, nextstate, alpha, gamma)
        
        # 新状态成为旧状态，进行下一轮迭代
        prev_state = nextstate
        # 记录每一步的得分
        r += reward
        # 游戏结束就跳出while循环
        if done:
            break
    # 一盘游戏结束，打印最终得分
    print("total reward: ", r)
    
    # 记录每轮游戏的reward
    r_record.append(r)
    
    # 计算Q-table的更新收敛情况
    error = 0
    for i in q:
        error = error + np.abs(q[i] - q_old[i])
    error_qa.append(error)
    q_old = copy.deepcopy(q) # 必须用深度拷贝，否则error恒为0
    
# 关闭游戏界面
env.close()

# 画收敛曲线
plt.figure(1,figsize=(10,10))
plt.plot(list(range(2000)),r_record[:2000],linewidth=0.8)
plt.title('Reword Convergence Curve',fontsize=15)
plt.xlabel('Iteration',fontsize=15)
plt.ylabel('Total Reword of one episode',fontsize=15)

plt.figure(2,figsize=(10,10))
plt.plot(list(range(2000)),error_qa[:2000],linewidth=0.8)
plt.title('Q-table difference Convergence Curve',fontsize=15)
plt.xlabel('Iteration',fontsize=15)
plt.ylabel('Error between old and new Q-table',fontsize=15)

# plt.savefig('2.pdf')

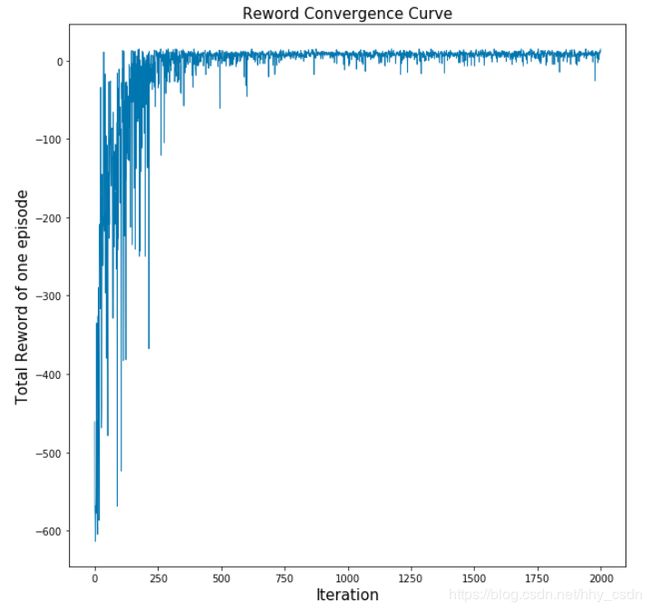
  最后画两个图，观察算法有没有收敛。

  第一个图是每个Episode总回报和训练代数（图中2000个Episode）的关系，一开始智能体完全不得要领，一局游戏玩下来扣600多分，随着训练进行，到最后平均一个Episode有+12分的total reward吧（个人感觉，没有经过统计）。图中看出收敛的趋势还是很明显的。

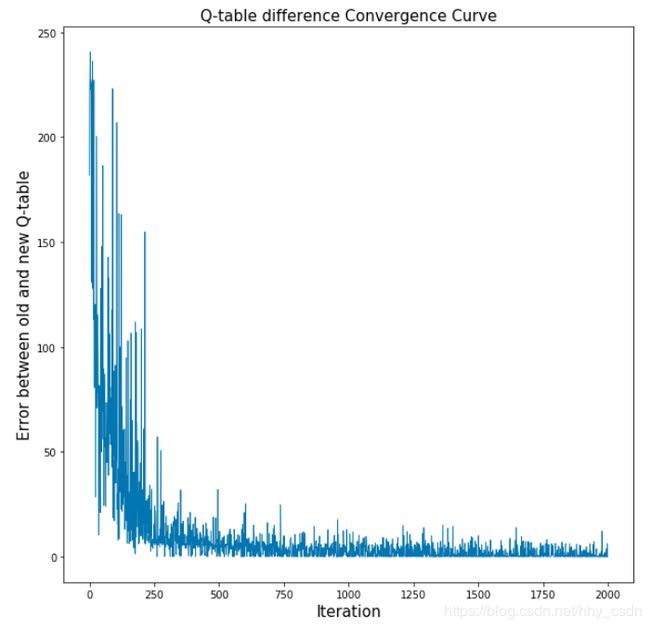
  第二个图是Q-table每次更新的时候，新旧Q-table之差的变化趋势。
$$error=\sum _{(s,a)\in \mathbf{S},\mathbf{A}}|Q_{new}(s,a)-Q_{old}(s,a)|$$
  图中显示，前250次迭代，Q-table的更新幅度较大，直到1000代左右逐渐收敛，新旧Q-table就基本不变了，这也可以表明算法的收敛性。