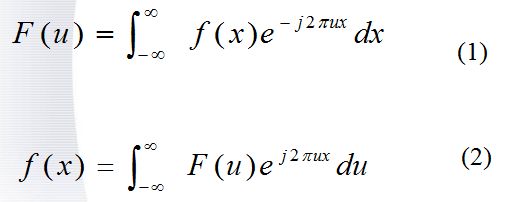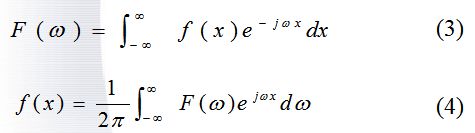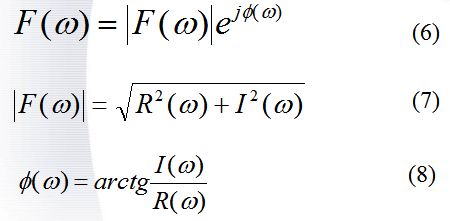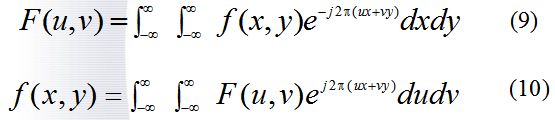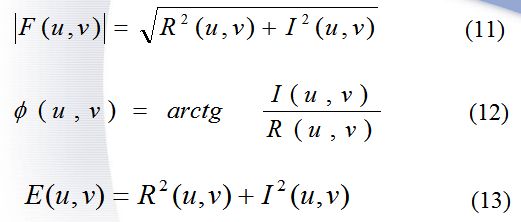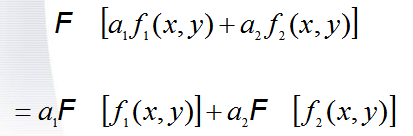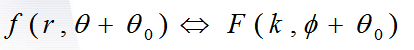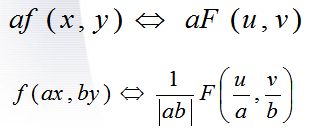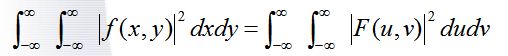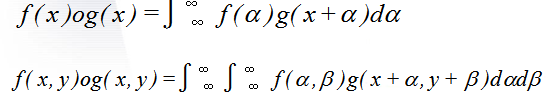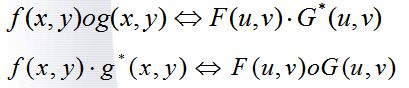傅立叶变换（一）
转自：http://blog.csdn.net/luoweifu/article/details/8246299
因为这些都是从《数字图像处理基础 . 阮秋琦》（注：这本书确实写的不错，虽然没有具体的算法实现，并且有些小错误，但是通俗易懂）里搬过来的，但又是进行图像傅丽叶变换之前需要了解的一些知识，所以不敢写原创，只能算是转载吧！如果想直接了解“图像傅丽叶变换”的算法实现请看下一章《傅丽叶变换（二）》
数字图像处理的方法主要分为两大类：
一个是空间域处理法(或称空域法)，
一个是频域法(或称变换域法)。
在频域法处理中最为关键的预处理便是变换处理。
目前，在图像处理技术中正交变换被广泛地运用于图像特征提取、图像增强、图像复原、图像识别以及图像编码等处理中。
傅里叶变换是大家所熟知的正交变换。在一维信号处理中得到了广泛应用。把这种处理方法推广到图像处理中是很自然的事。下面从傅丽叶的基本概念讲起，再讲图像处理中的傅丽叶变换算法实现。
一维傅里叶变换
定义
傅里叶变换在数学中的定义是严格的。设f(x)为x的函数，如果满足下面的狄里赫莱条件：
（１）具有有限个间断点；
（２）具有有限个极值点；
（３）绝对可积。
则有下列二式成立
式中x是时域变量，u为频率变量。
如令
， 则有
通常把以上公式称为傅里叶变换对。
函数f(x)的傅里叶变换一般是一个复数，它可以由式（5）表示
或写成指数形式
把|F(x)|叫做f(x)的傅里叶谱，而
叫相位谱。
傅丽叶变换的几个概念：
（１）只要满足狄里赫莱条件，连续函数就可以进行傅里叶变换，实际上这个条件在工程运用中总是可以满足的。
（２）连续非周期函数的傅里叶谱是连续的非周期函数，连续的周期函数的傅里叶谱是离散的非周期函数。
二维傅丽叶变换
定义
傅里叶变换可推广到二维函数。如果二维函数f(x,y)满足狄里赫莱条件，那么将有下面二维付里哀变换对存在：
与一维傅里叶变换类似，二维傅里叶变换的幅度谱和相位谱如下式
式中：F(u,v)是幅度谱；
是相位谱；E(u,v)是能量谱。
傅里叶变换的性质
傅里叶变换有许多重要性质。这些性质为实际运算处理提供了极大的便利。这里，仅就二维傅里叶变换为例列出其主要的几个性质。
具有可分性
这个性质说明一个二维傅里叶变换可用二次一维傅里叶变换来实现。
线性
傅里叶变换是线性算子，即
共轭对称性
如果F(u, v)是f(x, y)的傅里叶变换，F*(-u, -v)是f(-x, -y) 傅里叶变换的共轭函数，那么
F(u, v) = F*(-u, -v)
旋转性
如果空间域函数旋转的角度为
，那么在变换域中此函数的傅里叶变换也旋转同样的角度，即
比例变换特性
如果F(u, v) 是f(x, y)的傅里叶变换。a和b分别为两个标量，那么
帕斯维尔（Parseval）定理
这个性质也可称为能量保持定理。如果F(u, v) 是f(x, y)的傅里叶变换，那么有下式成立
这个性质说明变换前后并不损失能量
相关定理
如果，f(x),g(x)为两个一维时域函数；f(x,y)和g(x,y)为两个二维空域函数，那么，定义下二式为相关函数
由以上定义可引出傅里叶变换的一个重要性质。这就是相关定理，即
式中F(u, v) 是f(x, y)的傅里叶变换，G(u, v)是g(x, y) 的傅里叶变换，G*(u, v)是G(u, v)的共轭，g*(x, y)是g(x, y)的共轭。
卷积定理
如果f(x)和g(x)是一维时域函数，f(x,y)和g(x,y)是二维空域函数，那么，定义以下二式为卷积函数，即
由此，可得到傅里叶变换的卷积定理如下
式中 F(u,v) 和 G(u,v) 分别是f(x)和g(x)的傅里叶变换。