Python 数据结构笔记（1）：Python数据结构的性能

本系列博客是阅读《Problem Solving with Algorithms and Data Structures using Python》的笔记，原文链接

1、列表 List

索引和赋值是两个非常常用的操作。这个两个操作不论列表多长，它们的时间复杂度都是 $O(1)$。另一个非常常用的程序操作是去扩充一个列表。这有两种方式去生成一个更长的列表。我们可以用 append 操作或者 + 串联运算符。这个 append 操作的时间复杂度也是 $O(1)$。然而，+ 串联运算符是 $O(k)$，这里 $k$ 是指正在被连接的列表的大小。了解它对我们非常重要，选择正确工具可以使我们的程序更加有效。

让我们来看一下四种不同的方法来生成从 0 到 n 的列表。首先，

• 我们尝试用 for 循环体通过串联生成一个列表，
• 然后我们可以用“ append”代替串联操作。
• 接下来， 我们可以使用列表解析来生成一个列表。
• 最后，也许是最明显的方法，通过列表结构体的访问来使用 range 的功能。

下面展示了生成列表四种方法的代码：

def create_list_1_1():
    a_list = []
    for i in range(1000):
        a_list = a_list + [i]
        
def create_list_1_2():
    a_list = []
    for i in range(1000):
        a_list += [i]
        
def create_list_2():
    a_list = []
    for i in range(1000):
        a_list.append(i)
        
def create_list_3():
    a_list = [i for i in range(1000)]

def create_list_4():
    a_list = list(range(1000))

为了计时，我们需要 timeit 模块的 Timer 计时器， Timer 默认运行次数是一百万次。运行结束后，它将以浮点数的形式返回运行的总时间（单位：秒）。当你执行程序一次时，它返回的结果是以微秒为单位的。我们也可以在 timeit 中附上一个名叫 number 的参数，这样我们就可以指定程序被执行的次数。 下面将展示对每一个程序执行 1000 次所需要花费的时间

from timeit import Timer
t1 = Timer('create_list_1_1()', 'from __main__ import create_list_1_1')
print("concat 1 ",t1.timeit(number=1000), "milliseconds")
t1 = Timer('create_list_1_2()', 'from __main__ import create_list_1_2')
print("concat 2 ",t1.timeit(number=1000), "milliseconds")
t1 = Timer('create_list_2()', 'from __main__ import create_list_2')
print("append ",t1.timeit(number=1000), "milliseconds")
t1 = Timer('create_list_3()', 'from __main__ import create_list_3')
print("comprehension ",t1.timeit(number=1000), "milliseconds")
t1 = Timer('create_list_4()', 'from __main__ import create_list_4')
print("list range ",t1.timeit(number=1000), "milliseconds")

运行结果如下：
concat 1 1.3361934975348504 milliseconds
concat 2 0.07323397665902576 milliseconds
append 0.07901547132075848 milliseconds
comprehension 0.0323528873949499 milliseconds
list range 0.012585064675363355 milliseconds

我们可以看到，类表推导式确实是运算速度最快的方法。由于 a_list = a_list + [i] 会返回新的列表，它的执行速度是最慢的。下表展示了所有列表基本操作的大 $O$ 效率。在你对下表进行仔细思考后，可能会对 pop 操作的两个不同的时间复杂度感到疑惑。当 pop 操作每次从列表的最后一位删除元素时复杂度为 $O(1)$，而将列表的第一个元素或中间任意一个位置的元素删除时，复杂度则为 $O(n)$。这样迥然不同的结果是由 Python 对列表的执行方式造成的。在 Python 的执行过程中，当从列表的第一位删除一个元素，其后的每一位元素都将向前挪动一位。你可能觉得这种操作很愚蠢，但你会发现这种执行方式会让 index 索引操作的复杂度降为 $O(1)$，显然索引更常在程序中被使用。

Operation	Big-O Efficiency
index []	O(1)
index assignment	O(1)
append	O(1)
pop()	O(1)
pop(i)	O(n)
insert(i,item)	O(n)
del operator	O(n)
iteration	O(n)
contains (in)	O(n)
get slice [x:y]	O(k)
del slice	O(n)
set slice	O(n+k)
reverse	O(n)
concatenate	O(k)
sort	O(n log n)
multiply	O(nk)

2、Dict 字典

Python 中第二个主要的数据结构是字典。回想一下，字典与列表的不同之处在于你需要通过一个键（key）来访问条目，而不是通过一个坐标。字典条目的访问和赋值都是 $O(1)$ 的时间复杂度。字典的另一个重要的操作是所谓的“包含”。检查一个键是否存在于字典中也只需 $O(1)$ 的时间。其他字典操作的时间效率都已经在下表中列出。需要注意的是，这里所列出的都是平均时间复杂度。在一些罕见的情况下，包含、访问和赋值都可能退化为 $O(n)$

operation	Big-O Efficiency
copy	O(n)
get item	O(1)
set item	O(1)
delete item	O(1)
contains (in)	O(1)
iteration	O(n)

下一个性能实验将会对比列表和字典的包含操作的效率。在这一过程中我们将会验证列表的 in 操作是 $O(n)$，而字典的是 $O(1)$。这个实验很简单，我们将生成一个自然数（range）的列表，然后随机地选取一个数字，检查其是否在列表中。如果我们之前的效率表是正确的话，列表越大，所用的时间也就越长。然后我们将在一个以数字为键的字典上重复这个实验。这次我们会发现检查一个数字是否在字典中要快得多，而且即使字典变大，查询所用的时间也保持不变。

import timeit
import random
nums = []
lst_times = []
d_times = []
for i in range(10000,1000001,20000):
    t = timeit.Timer("random.randrange(%d) in x"%i,
                     "from __main__ import random,x")
    x = list(range(i))
    lst_time = t.timeit(number=1000)
    x = {j:None for j in range(i)}
    d_time = t.timeit(number=1000)
    nums.append(i)
    lst_times.append(lst_time)
    d_times.append(d_time)
    print("%d,%10.3f,%10.3f" % (i, lst_time, d_time))

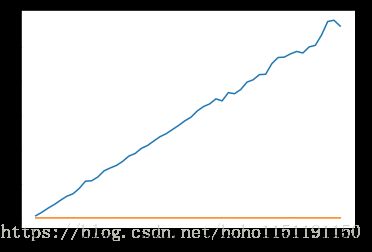
运行结果对比：随着列表的增大，其 in 操作所需要的时间是线性增长的，这证实了我们之前关于其时间复杂
度是 $O(n)$ 的论断。与此同时，字典的 in 操作用时保持不变，即使字典的大小不断变大也是如此。