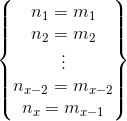tensorflow中高维度矩阵的乘法

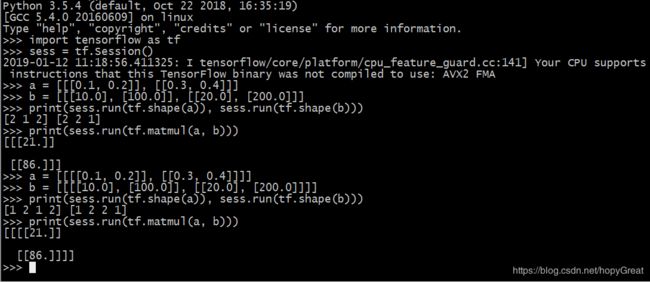
简单看个例子：

这里的结果是怎么来的呢？

仔细分析下，不难得出：

21 = 10 * 0.1 + 100 * 0.2，

86 = 20 * 0.3 + 200 * 0.4， 

所以，虽然变成三维了，但实际还是做的二维运算。

高于二维的维度，挨个遍历，便可得到一个二维矩阵，对这两个二维矩阵进行线性代数里的矩阵乘法。

这样就要求了两个高维矩阵相乘必须满足的一些维度关系了。

对于两个高维矩阵，a（维度为（n1 * n2 * n3 * ... * nx-1 * nx）），b（维度为（m1 * m2 * m3 * ... * mx-1 * mx））。

则应有：

也就是前面的高于二维的维度必须相等，二维内的维度，应该满足线性代数矩阵乘法的要求，即前一个矩阵的列数等于后一个矩阵的行数。

再加个简单的验证，把前面那个例子，再加一维。

 

 

最能证明这个运算的例子，应该就是CNN中的多通道卷积操作了吧。

多通道卷积操作要求了，卷积核的通道数应该和输入数据的通道数保持一致。