论文解读：Multi-view Clustering via Joint Nonnegative Matrix Factorization

摘要

很多真实世界中的数据集由不同表达和视角组成，这些不同的表达和视角的信息往往互为补充。为了整合非监督集合中多个视角的信息，多视觉聚类算法同时聚类不同视角以得到一个聚类结果，这个结果揭示了多个视觉共享一个潜在结构。本文我们提出了一个NMF（基于非负矩阵分解）的多视角聚类算法，该算法寻找一个因式分解，使得多个视角给出一致的聚类结果。本文提出算法的关键在对有约束的联合非负矩阵因式分解过程进行公式化，该分解过程的约束使得每个视角在分解过程趋向一致的结果。主要的问题是如何保持聚类结果在不同视角的是有意义和可比较的。为了解决这个问题，我们基于NMF和PLSA的关系设计了一个新型的高效归一化策略。几个数据集上的实验结果表明了我们方法的可靠性。

1 简介

现实中的很多数据集由不同的表达和视角组成。例如，同一个故事可以被不同的文章讲述；一个文件可以被翻译为多种不同的语言；研究团队可以由不同的研究课题组成，也可以看做由不同的作者组成；网页可以基于内容分类，也可以基于超链接文本等等。在这些数据中，每个数据集被不同的属性表达，这些属性可以自然地分成不同的子主题，每个子主题都提供了足够挖掘的信息。由于这些不同的表达往往含有兼容互补的信息，我们很自然地想到将这些信息整合在一起以得到更好的性能。从多视角中学习的关键在于如何利用每个视角自己的信息以得到更好的表现而不仅仅串联这些信息。
现实生活中无标签数据非常多，而且越来越多以来自不同来源的多个不同视角出现。因此，无标签数据不同视角的非监督学习，即多视角聚类，得到了很多的关注。多视角聚类的目标是依据基于物体的多个视角的表达将物体分到某一类。现有的多视角聚类算法可以大致分为三类：第一类方法将多视角整合到聚类过程是直接在在优化特定损失函数时进行；相反地，第二类，比如基于典型相关性分析的一类，先将多个视角投影到一个共同的低维子空间，然后再应用其他的聚类算法进行聚类；第三类称为晚整合或者晚融合，聚类结果先由每个独立的视角得到，最后根据一致性把结果融合。
在本文中，我们提出一个新的多视角聚类算法，该算法基于一个非常高效的单视角聚类算法——非负矩阵分解（NMF）。NMF一开始是作为一种降维技术出现，在信息检索和模式识别领域应用广泛。NMF在应用中有着直观的解释，例如，我们可以将每一个观测到的视角看做是非负基向量的线性组合。近年来，NMF成为数据聚类中一种很受欢迎的技术，且得到目前最好的一些结果。
由目前所见的工作，NMF可以产生较高级的聚类结果（易于解释的结果），因此如有基于NMF的多视角聚类方法将会非常有用。现有的应用NMF到多视角聚类的主要问题在于如何在多个视角上同时得到有意义，可比较的聚类结果。其次，传统的用于NMF中的归一化策略在多视角情境下变得困难，或者得不到有意义的聚类结果。在该文章中，我们通过提出一个新型的归一化策略，并遵循代表聚类结构的因子必须规范到一致的原则解决这些问题。
我们提出的算法的优点有：
1、第一个提出基于联合NMF的多视角聚类算法。不像传统方法一样只是简单固定多个视角共享的单一因子。
2、如上所述，现有的标注NMF的归一化无法保证来自不同视角的因子的可比较性和有意义，使得融合变得困难。为了解决这个问题，我们受NMF和PLSA间关系的启发，提出了一个新型的归一化过程。
3、提出一个可扩展的收敛的迭代优化的框架。整体算法效果比目前最好的算法提高了6个百分点。
文章接下来的结构如下：
第二部分先简单回顾NMF和PLSA的关系。
第三部分提出多视角NMF算法。
第四部分是实验。
第五部分是对相关工作的一个讨论。
第六部分是总结。

2 NMF和PLSA的回顾

NMF的目的是找到两个非负矩阵 U 和 V 使得下式成立：

X≈UVT(2.1)

这个重建过程可以抽象为一个 frobenius 范数优化问题：

minU,V||X−UVT||2F, s.t.U≥0,V≥0

易知上式非凸，因此难以找到一个全局最优解。有文献给出“乘法更新法则”，可以迭代地最小化目标函数：

Ui,k←Ui,k(XV)i,k(UVTV)i,k,Vi,k←Vi,k(XU)i,k(VUTU)i,k(2.2)

NMF的抽象化式子（2.1）不止有一个解，若存在可逆矩阵 Q ，则有：

X≈UVT=(UQ−1)(QV−1)(2.3)

因此在聚类中要加上一些约束使得聚类结果唯一。
接着介绍NMF和PLSA的关系， 这两者的关系使NMF做聚类变得有意义。
PLSA是用于文本分析的一个主题模型。PLSA认为，词语-文本共生矩阵 X （矩阵中的元素 Xij 表示单词 wi 和文本 dj 的共生数量）由具有 K 个主题的混合模型产生：

p(w,d)=∑k=1KP(w|k)P(d,k)

上式的参数由最大似然法估计得到。
假设 ||X||1=1 ，若矩阵 Q 是一个对角矩阵且 Qk,k=∑iUi,k 。则已有文献证明，在满足上述条件的情况下， (UQ−1) （或者 (QVT) ）拥有条件概率矩阵 P(w|k) （或者 P(d,k)T ）的性质。这提供了将NMF用于聚类的理论基础。特别地，在聚类公式化中， V 的每一行表明了数据点 i 属于类别 k 的程度。注意到 ||QVT||1 近似于1（因为 ∑P(d,k)=1 ）,这个性质可以被下式证明：

||X||=||∑jXj||≈∑k=1K||U.,k∑jVj,k||=∑k=1K||∑jVj,k||=||V||

则 QVT 的作用与一个聚类指示矩阵相似，其每一列代表着一个数据点和不同类别的联合概率。

3 多视角非负矩阵分解

在这部分中，我们对提出的用于多视角聚类的联合矩阵分解进行数学建模，并且给出了一个搞笑的迭代更新法则以得到最优解。
我们理论的前提：一个数据的不同视角很大的概率会被分到同一类别。
因此，在矩阵分解方面，我们需要让从不同视角学习到的系数矩阵被松约束到一致。这个一致性矩阵则反映了不同视角共享的潜在聚类结构。
另外，为了保证分解的唯一性和准确性，需要在优化过程进行规范化。传统的用于NMF中的规范化很难再多视角集合中被优化，或者难以产生有意义的聚类结果，使得不同视角的融合变得困难和不确定。因此我们设计了一个新型的归一化过程，特别地，我们在优化过程对基向量做 l1 规范化。这基于上节提到的NMF和PLSA的关系，这样的规范化使得不同视角的系数矩阵有了概率意义，对聚类来说可比较且有意义。

3.1 目标函数

对于每一个视角 X(v) 有 X(v)=U(v)(V(v))T 。
在传统的NMF中，系数向量 V(v)j,. 可以看做是第 j 个数据点基于基矩阵 U(v) 的低秩表达。这里对于不同的视角，我们有一样数量的数据，但是每个视角可能对应不同数量的特性。因此系数矩阵 V 维数保持一致，但是基矩阵不一定一致。
下面的损失函数作为系数矩阵 V(v) 和一致性矩阵 V∗ 之间差异性的测量：

D(V(v),V∗)=||V(v)−V∗||2F

来自不同视角的 V(v) 不一定可比较且对聚类有意义，因为从公式（2.3）可以看到，任何可逆矩阵 Q 和 V(v) 的乘积依旧是问题的解。为了使得这个差异性测量对于不同的 V(v) 适应，且理论上对聚类有意义，一个可能的解决方案就是归一化 V(v) 并计算其跟一致性矩阵 V∗ 的距离。然而，这样的归一化会让优化难以处理。为了解决这一问题，我们在基向量 U(v).,k 上加 l1 规范化约束。这样，在 ||X||=1 的前提下 ||V(v)|| 约等于1（上一节已证明）。不同视角的 V(v) 处于同一范围后， V(v) 和 V∗ 的比较变得合理。另外，讲过规范化， V(v) 可以视为 P(d,k)(v) ，故它的每一个元素都概率可解释，这样也使得 V∗ 的每一个元素在聚类中也概率可解释，比如，矩阵 V∗ 的每一个元素是来自不同视角的 P(d)(v) 加权的 P(k|d)(v) 的一致。
将上述方法和用于每个独立视角的NMF框架融合，可得到下面的关于 U(v) ， V(v) ， V^* V∗ ， 1\le v \le n_v 1≤v≤nv 的联合最小化问题：
\sum _{v=1}^{n_v}||X^{(v)}-U^{(v)}(V^{(v)})^T||_F^2+\sum _{v=1}^{n_v}\lambda _v||V^{(v)}-V^*||_F^2\qquad (3.4)\\ s.t. \forall 1\le k \le K,||U^{(v)}_{.,k}||_1=1且U^{(v)},V^{(v)},V^*\ge 0

∑v=1nv||X(v)−U(v)(V(v))T||2F+∑v=1nvλv||V(v)−V∗||2F(3.4)s.t.∀1≤k≤K,||U(v).,k||1=1且U(v),V(v),V∗≥0

其中， λv 是提出的算法的唯一一个参数，不但调节了不同视角的权重，还调节了标准NMF重构误差和差异项 D(V(v),V∗) 的权重。 λv 的选择将在实验部分讨论。
对 U(v) 的约束可以通过引入辅助变量来实现：

Q(v)=Diag(∑i=1MUvi,1,∑i=1MUvi,2,...,∑i=1MUvi,K)(3.5)

结合式（2.3）和式（3.4）可以得到下面的目标函数：

O=∑v=1nv||X(v)−U(v)(V(v))T||2F+∑v=1nvλv||V(v)Q(v)−V∗||2F(3.6)s.t.∀1≤v≤nv,||U(v).,k||1=1且U(v),V(v),V∗≥0

为了解决式（3.6）我们提出了一个可收敛的迭代更新过程。迭代进行以下两个步骤知道收敛：（1）固定 V∗ ，基于 U(v),V(v) 最小化 O ，（2）固定 U(v),V(v) ，基于 V∗ 最小化 O 。

这里对整个具体的解法过程不再翻译，算法的步骤如下：

基于NMF和PLSA的关系，提出的算法有很好的概率解释：矩阵 V∗ 的每一个元素相当于是经过来自不同视角的 P(d)(v) 加权的 P(d|k)(v) 。因此，该算法对于来自不同聚类的数据点在向量空间不沿着同一方向的数据集特别有效。比如，主题模型算法中，文档-词语共生矩阵拥有这个特性，故可以被这个方法建模。
然而，没有上述提到的性质的数据，可以直接在 V∗ 上运用k近邻算法，因为 V∗ 是原始数据点的一个潜在表达。

4 实验

4.1-4.3

实验部分采用了一个合成的数据集和三个真实数据集3-Sources，Reuters，Digit，分别将文章提出的MultiNMF算法与已有的NMF或聚类方面的算法对比，包括BSV，ConcatNMF，ColNMF，Co-reguSC，结果显示，在精确度和归一化互信息两个指标下，文章提出的算法均得到了最好的结果。

4.4 λ(v) 参数学习

λ(v) 是每一个视角的权重，反映了每一个视角的重要性，如果已知一些先验信息，可以加入 λ(v) 中。较大的 λ(v) 将会使得各个视角的 V 趋向一致，较小的 λ(v) 使得目标函数无法容忍矩阵分解的误差。实验中为了比较的可信度，我们设置各个视角的 λ(v) 大小一致，MultiNMF算法在不同数据集下的精度随 λ(v) 的变化如下图：

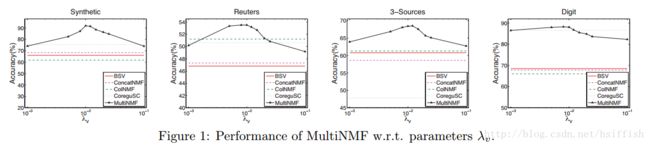
4.5 收敛性学习

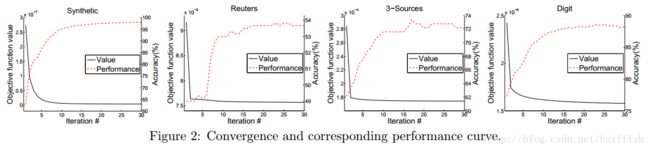
下图展示了实验中的收敛曲线。黑色实线是目标函数值，红色虚线是MultiNMF算法的精度，可以看到，大概15次迭代后算法收敛。

5 相关工作

相关工作阐述。讨论了三个用于光谱聚类的算法。

6 总结

该部分内容多于摘要和简介重合，不再赘述。