PRML读书笔记——线性回归模型

这一章从线性回归模型的基本形式出发，主要围绕线性基函数的回归模型展开，分析了最大似然估计和最小平方误差函数的关系、最小平方误差函数的几何意义、正则化的最小平方误差，然后用偏置-方差分解的角度理解正则化项；用贝叶斯的思想分析线性回归模型，介绍了模型证据的意义，最后分析线性回归模型的局限性

线性基函数模型

基础

回归问题的最简单模型是输⼊变量的线性组合：

y(x,w)=w0+w1x1+...+wDxD

这通常被称为线性回归，模型的关键是它既是 {wk} 的线性函数，也是输入变量 {xi} 的线性函数，虽然简单但是也带来了很大的局限性。

考虑将输⼊变量的固定的⾮线性函数进⾏线性组合，形式为：

y(x,w)=w0+∑j=1M−1wjϕj(x)

其中， ϕj(x) 被称为基函数，这个模型参数总数为M

这里 w0 是偏置参数，可以融入系数中，得：

y(x,w)=∑j=0M−1wjϕj(x)=wTx

现在， y(w,x) 是x的非线性函数，但它依然是 w 的线性函数，一般模型依然被称为线性模型

基函数选择有很多如

（1）径向基函数

ϕj(x)=exp{−(x−μj)22s2}

（2）sigmoid

σa=11+exp(−a)

最大似然与最小平方

现在线性回归的模型已经搭建出来，考虑求解，假设⽬标变量 t 由确定的函数 y(x,w) 给出，这个函数被附加了⾼斯噪声，即

t=y(x,w)+ϵ

假设噪声是零均值的高斯随机变量，精度为 β ，则对应的概率分布满足：

p(t|x,w,β)=N(t|y(x,w),β−1)

E[t|x]=∫tp(t|x)dt=y(x,w)

注意，这里有一个假设：给定x的条件下，t的条件分布是单峰的，这对于⼀些实际应⽤来说是不合适的。对于不同问题而言，这或许会是修改loss的起源之一。

那么，对于一个观测数据集 X={x1,...,xN} ，它对应的后验概率为：

p(t|x,w,β)=∑n=1NN(tn|wTΦ(xn),β−1)

然后构造似然函数

ln p(t|w,β)==∑n=1Nln N(tn|wTϕ(xn),β−1)N2ln β−N2ln(2π)−βED(w)

其中，平方和误差定义为：

ED(w)=12∑n=1N{tn−wTϕ(xn)}2

所以，平方和误差本身就是出自高斯分布的前提假设的。

对似然函数求导并令导数为0，可得到：

wML=(ΦTΦ)−1ΦTt

上式是最小平方问题的规范方程，其中 Φ 是 N×M 的设计矩阵，有：

Φ=⎛⎝⎜⎜⎜⎜⎜⎜⎜ϕ0(x1)ϕ0(x2)...ϕ0(xN)ϕ1(x1)ϕ1(x2)...ϕ1(xN)............ϕM−1(x1)ϕM−1(x2)...ϕM−1(xN)⎞⎠⎟⎟⎟⎟⎟⎟⎟

对应的偏置为：

w0=t⎯−∑j=1M−1wjϕj⎯⎯⎯⎯

其中

t⎯=1N∑n=1Ntn

ϕj⎯⎯⎯⎯=1N∑n=1Nϕj(xn)

这里，偏置 w0 补偿了⽬标值的平均值（在训练集上的）与基函数的值的平均值的加权求和之间的差。

同理

1βML=1N∑n=1N{tn−wTMLϕ(xn)}2

这里，到噪声精度的倒数由⽬标值在回归函数周围的残留⽅差给出

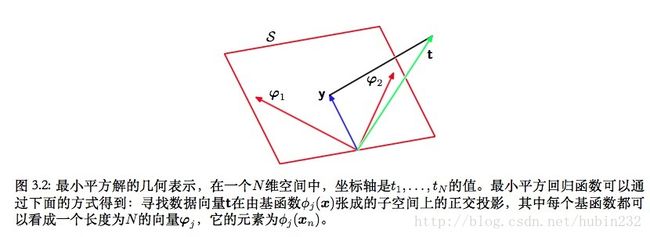
最小平方的几何描述

最小平方误差的几何意义是，目标变量投影到模型形成的超平面上，模型拟合的结果尽可能接近这个投影。这在一定程度上说明，最小平方误差不可能完全拟合所有的训练数据

正则化最小平方

可以通过添加正则化项的思想来控制过拟合，则总的误差函数变为：

E=ED(w)+λEW(w)=12∑n=1N{tn−wTϕ(xn)}2+12wTw

这是一个二次函数，直接求导并令导数为0即可得

w=(λI+ΦTΦ)−1ΦTt

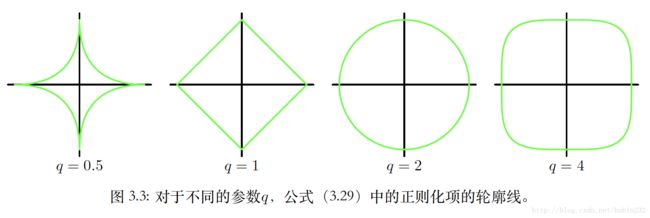
这里，L2番薯的正则化项又被称为脊回归或者权值衰减。上面的损失函数还可以写成更一般的形式：

12∑n=1N{tn−wTϕ(xn)}2+λ2∑j=1M∣∣wj∣∣q

不同的q值能得到不同的正则化函数轮廓线，

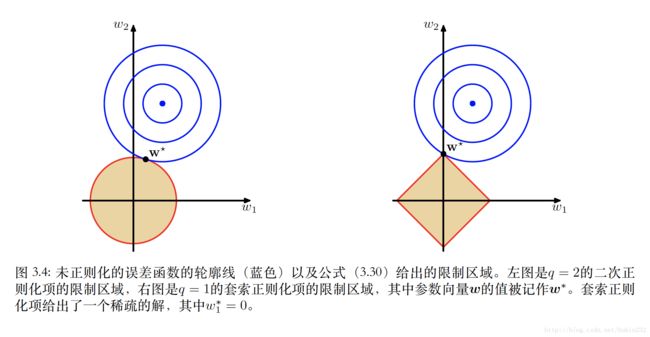
q=1时，被称为套索（lasso），这是很常用的一种正则化，如果 λ 充分⼤，那么某些系数 wj 会变为零，从⽽产⽣了⼀个稀疏模型，这个模型中对应的基函数不起作⽤。两种正则化项的对比如下图，图中的圆表示以目标变量t为中心，形成了平方差损失，显然越靠近中心表示越小（即越好），以原点为中心的是正则化项的形式，不同q产生不同的边界形状，当两个形状相交，表示w的一个解。而q=1时，往往在坐标轴上相交，所以就导致w有很多0

多输出

如果每个样本对应的标签数量 K>1 （目标变量记作目标向量t），则可以对于t的每个分量，引⼊⼀个不同的基函数集合，从⽽变成了多个独⽴的回归问题。而这里考虑的是使用一组相同的基函数来对目标向量的所有分量建模，如下

y(x,w)=WTϕ(x)

其中，其中 y 是⼀个 K 维列向量， W 是⼀个 M×K 的参数矩阵， ϕ(x) 是⼀个 M 维列向量，每个元素为 ϕj(x) ，并且与之前⼀样， ϕ0(x)=1 。现在假设目标向量的条件概率分布是各项同性的高斯分布，即

p(t|x,W,β)=N(t|WTϕ(x),β−1I)

则对于一组患侧 t1,...,tn ，对应的对数似然函数为：

ln p(T|X,W,β)==∑n=1Nln N(tn|WTϕ(xn),β−1I)NK2ln(β2π)−β2∑n=1N∥∥tn−WTϕ(xn)∥∥2

这样，可以得到最大似然的结果

WML=(ΦTΦ)−1ΦTT

偏置-方差分解

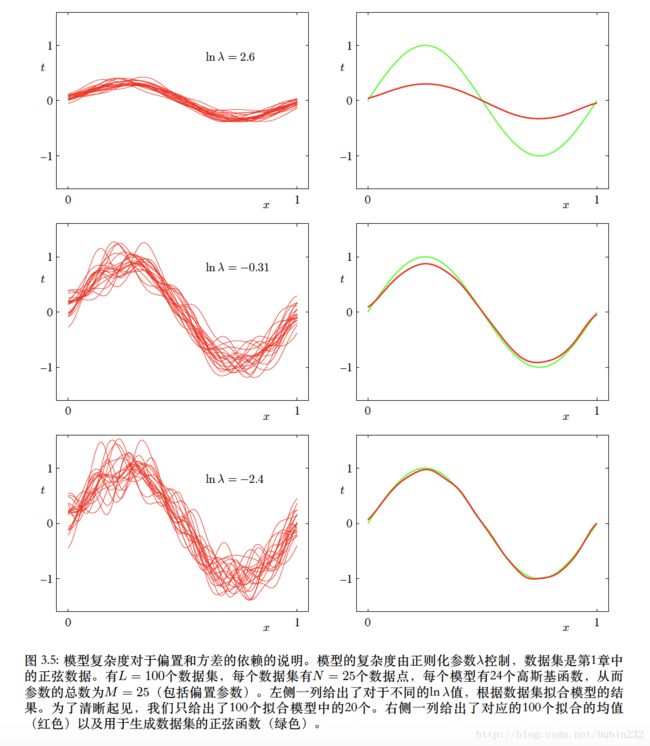
用最大似然发或者最小平方和误差求解回归问题会存在过拟合，正则化能抑制过拟合现象但是超参数不好取值。现在，用分解的方式考察超参数对模型的影响。

假设用平方损失函数求解回归问题，则最优的预测结果如下：

h(x)=E[t|x]=∫tp(t|x)dt

假设我们用 y(x,w) 建模，则平方损失函数的期望为：

E[L]=∫{y(x)−h(x)}2p(x)dx+∫∫{h(x)−t}2p(x,t)dxdt

现在，第二项与 y(x) 无关，是由数据本⾝的噪声造成的，表⽰期望损失能够达到的最⼩值。第⼀项与我们对函数 y(x) 的选择有关，我们要找⼀个 y(x) 的解，使得这⼀项最⼩。实际上，由于数据有限，我们不能够精确地知道 h(x)

现在假设有许多数据集，每个数据集的⼤⼩为N，并且每个数据集都独⽴地从分布 p(t,x) 中抽取。对于任意给定的数据集 D ，可以学习算法到⼀个预测函数 y(x;D) 。不同的数据集会得到不同的函数，从⽽给出不同的平⽅损失的值。这样，特定的学习算法的表现就可以通过取各个数据集上的表现的平均值来进⾏评估。

考虑是第一项被积函数，对于特定的数据集D，有

ED[{y(x;D)−h(x)}2]===ED[{y(x;D)−ED[y(x;D)]+ED[y(x;D)]−h(x)}2]ED[{{y(x;D)−ED[y(x;D)]}2+{ED[y(x;D)]−h(x)}2+2{y(x;D)−ED[y(x;D)]}{ED[y(x;D)]−h(x)}}]{ED[y(x;D)]−h(x)}2+ED[{y(x;D)−ED[y(x;D)]}2]

这里，第一项为平方偏置，表示所有数据集的平均预测与预期的回归函数之间的差异。第⼆项，被称为⽅差，度量了对于单独的数据集，模型所给出的解在平均值附近波动的情况，因此也就度量了函数 y(x;D) 对于特定的数据集的选择的敏感程度

也就是我们得到了期望平方损失的分解：

期望损失=偏置2+方差+噪声

其中

偏置2=∫{ED[y(x;D)]−h(x)}2p(x)dx

方差=∫ED[{y(x;D)−ED[y(x;D)]}2]p(x)dx

噪声=∫∫{h(x)−t}2p(x,t)dxdt

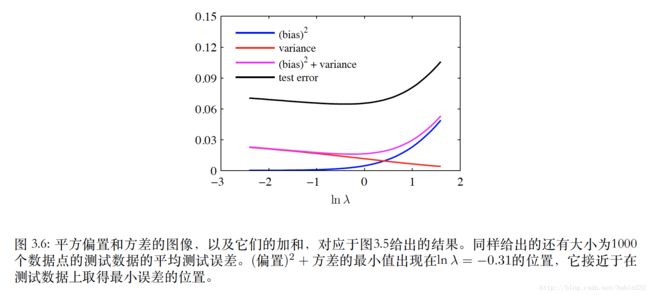
公式可以看到，偏置和方差存在折中，对于灵活的模型，偏置较⼩，⽅差较⼤。对于固定的模型，偏置较⼤，⽅差较⼩。有着最优预测能⼒的模型时在偏置和⽅差之间取得最优的平衡的模型。

那么它和正则化超参数有什么关系呢，正则化的超参实际控制着这种平衡的关系，正则化系数大，则它要求不过过于拟合现有数据，因此不同数据得到的方差小，偏置大；反之，数据会相对拟合已有数据，不同数据集得到的模型预测方差大，但各个模型对自身的数据偏置小

贝叶斯线性回归

这里讲从贝叶斯的角度求解线性模型，它能避免最大似然的过拟合问题，也会引出使用训练数据本身确定模型复杂度的自动化方法

参数分布

所谓贝叶斯方法就是先假设参数的一个已知先验，然后求解后验概率的方法。这里假设模型参数 w 服从高斯分布

p(w)=N(w|w0,S0)

则对应的后验概率必然满足高斯分布

p(w|t)=N(w|mN,SN)

其中

mN=SN(S−10m0+βΦTt)

S−1N=S−10+βΦTΦ

这里为了简单起见，假设先验分布为各向同性的高斯分布：

p(w|α)=N(w|0,α−1I)

则对应后验的参数为：

mN=βSNΦTt

S−1N=αI+βΦTΦ

我们知道，后验概率分布可以由对数似然函数和先验的乘积得到，而回归问题的对数似然函数是一个高斯形式，因而把后验看做 w 的函数，两边取对数即可得：

ln p(w|t)=−β2∑n=1N{tn−wTϕ(xn)}2−α2wTw+const

这也就是说，以贝叶斯的观点分析回归问题，因为它存在的先验假设，使得模型本身考虑了正则化参数的情况。

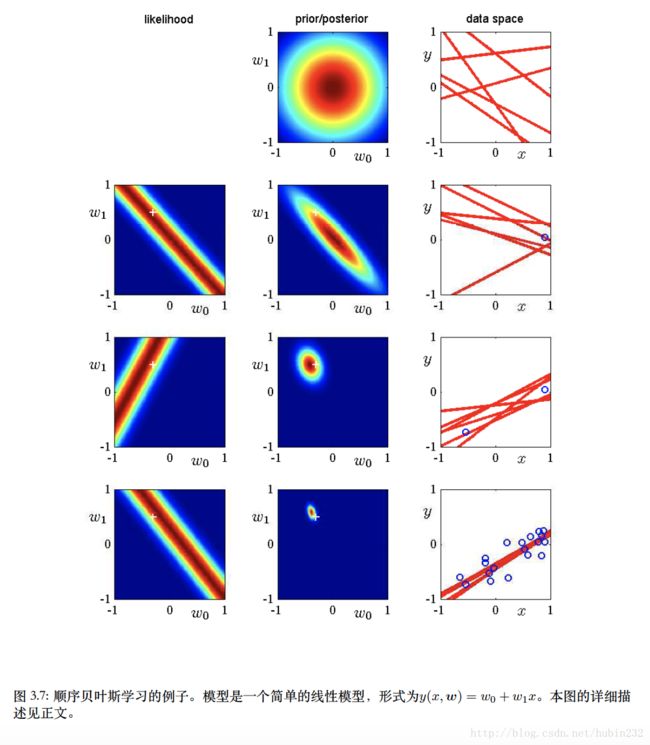
作者在这里还举了个顺序学习的例子。假设线性回归模型为 y(x,w)=w1x1+w2x2 ，则只有两个参数。现在我们初始化后，先得到参数空间的先验分布和后验分布。当新数据点被观测时，计算对应的似然函数，而上一轮的后验分布被当做先验分布，两者相乘得到当前轮的后验分布，以此类推，如下图

（2）预测分布

p(t|t,α,β)=∫p(t|w,β)p(w|t,α,β)dw

如果考虑 p(w|t)=N(w|wN,SN) ， p(t|x,w,β)=N(t|y(x,w),β−1) ，则有：

p(t|x,t,α,β)=N(t|mTNϕ(x),σ2N(x))

其中

σ2N(x)=1β+Φ(x)TSNΦ(x)

等价核

对于高斯分布的先验而言，得到的后验恰好也是高斯分布，最大后验的权向量结果必然是 wMAP=mN ，所以，现在预测均值可以写成：

y(x,mN)=mTNϕ(x)=βϕ(x)TSNΦTt=∑n=1Nβϕ(x)TSNϕ(xn)tn

所以可以写成核的形式

y(x,mN)=∑n=1Nk(x,xn)tn

其中

k(x,x′)=βϕ(x)TSNϕ(x′)

这个函数被称为平滑矩阵或者等价核

贝叶斯模型比较

过拟合是机器学习中常见的问题之一，指的是一个模型由于过度复杂造成在训练集中表现良好而在测试集中表现很差的现象，通常是由于参数过多导致数据相对变小造成的。这是因为在采用极大似然估计的方式进行参数的点估计的时候，复杂的模型总是拟合出更好的结果。但是由于模型过于复杂，它的泛化能力并不一定好。频率派通常采用加一个正规项和交叉验证的方式处理过拟合问题。与此相对的贝叶斯学派用贝叶斯的方法给出一种自然的方法进行模型选择, 找到一个复杂度适中的模型,同时避免了过拟合和欠拟合问题，不需要预先留出一部分数据进行验证。

模型⽐较的贝叶斯观点仅仅涉及到使⽤概率来表⽰模型选择的不确定性，以及恰当地使⽤概率的加和规则和乘积规则。

假设我们想⽐较L个模型 {Mi} ，其中 i=1,...,L 。这⾥，⼀个模型指的是观测数据 D 上的概率分布。我们假设数据是由这些玩模型中的一个生成的，但不知道究竟是哪一个，这种不确定性通过先验概率分布 p(Mi) 表示，现在我们想估计对应的后验分布：

p(Mi|D)∝p(Mi)p(D|Mi)

其中， p(D|Mi) 是模型证据，它表达了数据展现出的不同模型的优先级。两个模型的模型证据的比值 p(D|Mi)p(D|Mj) 被称为贝叶斯因子。

现在，假设模型由一个参数 w 控制，则模型证据为：

p(D|Mi)=∫p(D|w,Mi)p(w|Mi)dw

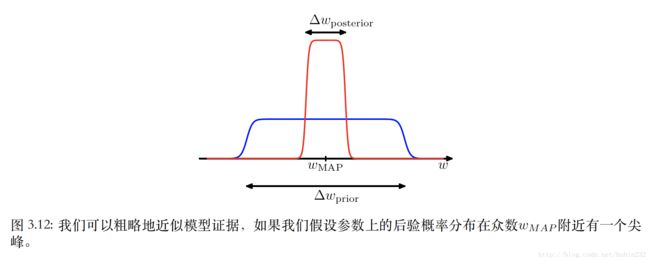
下面考虑一种对积分的近似方法。假设后验分布在最⼤似然值 wMAP 附近是⼀个尖峰，宽度为 △w后验 ，那么可以⽤被积函数的值乘以尖峰的宽度来近似这个积分。如果进⼀步假设先验分布是平的，宽度为 △w先验 ，即 p(w)=1△w先验 ，那么有

p(D)=∫p(D|w)p(w)dw≃p(D|wMAP)△w后验△w先验

取对数，有

ln p(D)≃ln p(D|wMAP)+ln △w后验△w先验

这里，第⼀项表⽰拟合由最可能参数给出的数据。对于平的先验分布来说，这对应于对数似然。第⼆项⽤于根据模型的复杂度来惩罚模型

如果考虑一个有M个参数的模型，则有：

ln p(D)≃ln p(D|wMAP)+Mln △w后验△w先验

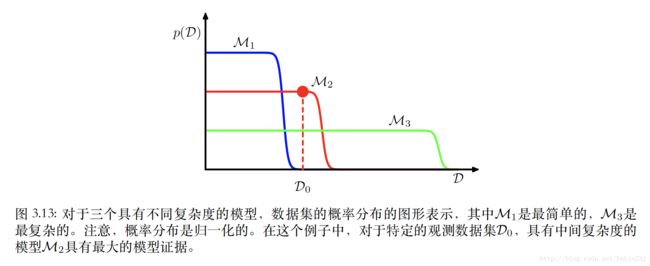
复杂度惩罚项的⼤⼩随着模型中可调节参数M的数量线性增加。随着我们增加模型的复杂度，第⼀项通常会增⼤，因为⼀个更加复杂的模型能够更好地拟合数据，⽽第⼆项会减⼩，因为它依赖于M。由最⼤模型证据确定的最优的模型复杂度需要在这两个相互竞争的项之间进⾏折中。

优点：避免了过拟合的问题，并且使得模型能够基于训练数据⾃⾝进⾏对⽐。

缺点：需要对模型的形式作出假设，并且如果这些假设不合理，那么结果就会出错。

对于线性基函数模型，如果用贝叶斯方法求解，会难以求出参数 w 的解析解，书中提供了相应的近似方法，大致意思是引入超参数，对超参数做相关近似，然后得到目标变量关于超参数的似然函数，按照似然估计的方法求解。这里省略讨论

固定基函数的局限性

局限性的来源是我们假设了基函数在观测到任何数据之前就被固定了下来

局限性：

（1）基函数难以估计

（2）数据维数很大，基函数的数量会随着输入空间的维度D迅速增长，而且通常是指数方式的增长

真实数据的性质可能帮助缓解这种潜在的维度灾难：

（1）输入变量往往存在相关性

（2）目标变量可能只依赖于数据流形中的少量可能的方向