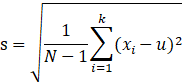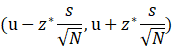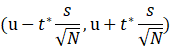python绘图：柱状图绘制详解

        柱状图用于反映数值变量的集中趋势，用误差线估计变量的差值统计。理解误差线有助于我们准确的获取柱状图反映的信息，因此打算先介绍一下误差线方面的内容，然后介绍一下利用seaborn库绘制柱状图。

1.误差线的理解

       误差线源于统计学，表示数据误差(或不确定性)范围，以更准确的方式呈现数据。当label上有一组采样数据时，一般将这组数据的平均值作为该label上标注的值，而用误差线表示该均值可能的误差范围。误差线可以用标准差(standard deviation,SD)、标准误(standard error,SE)和置信区间表示，使用时可选用任意一种表示方法并作相应说明即可。当label上值有一个数据时，则不需要标注误差线。

• 标准差

       在实际中，总体的标准差总是未知的，我们一般用样本标准差来估计总体标准差，样本标准差定义为 

                                                                      

      其中为样本均值，则误差线的范围为()

• 标准误

       当多次进行重复采样时，会得到多组数据，每组数据都有一个平均值，这些平均值间是有差异的，尽管在每组数据量较大时，这个差异会比较小，标准误表示的就是平均值的误差范围。可以对标准误做以下估计

                                                                            

       其中为样本的标准差，则误差线的范围为()

• 置信区间

       由于bar上标明的值是样本均值，这里实际上是对样本均值进行区间估计得到的置信区间。一般作区间估计时，需要先获知总体的分布，在实际中我们依据样本的数据量来假设其总体的分布。当为大样本数据情况时(一般数据量大于30),假设样本服从正态分布，当数据量较小时(小于30)时假设样本服从-分布。当然，若已知总体分布时则不需要假设，包括接下来均值及标准差的计算，若已知时则不需要对其进行估计。

       当总体为正态分布时，误差线的范围为

                                                                     

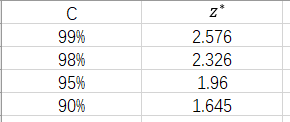
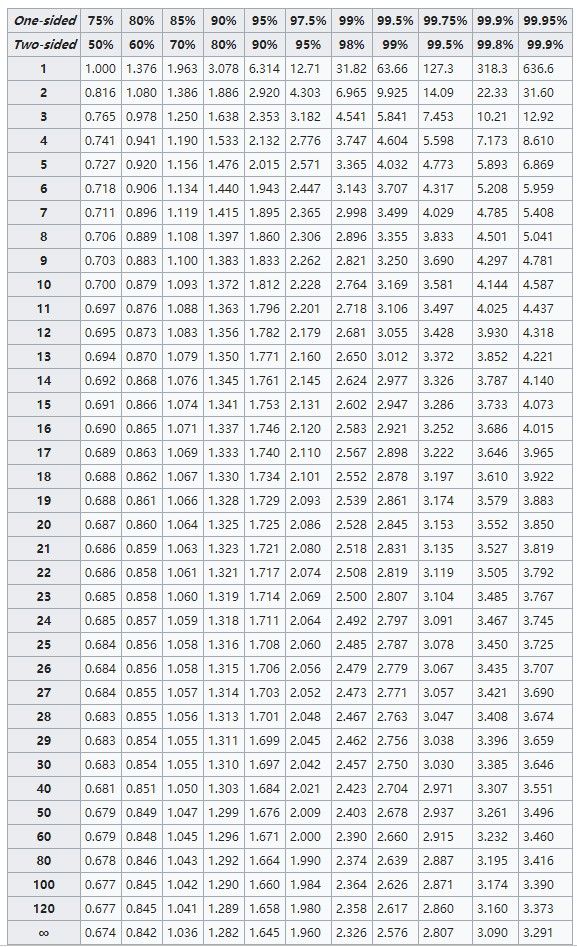
       其中依据区间置信度来计算,C表示置信度(只列出常见的置信度)

                                                           

       当总体为-分布时，误差线的范围为

                                                                       

       其中依据置信度及样本自由度(N-1)来计算，一般查询-分布得到

                                 

                                                          

       这里以均值的置信区间为例，顺便说一下对置信区间的理解。置信区间(置信度为)是指在重复采集次时，得到的样本均值有次可能落在置信区间内，我们不能对置信区间作如下解读：总体均值有的可能性在置信区间内，这是不对的，在一次采样完成后，按照频率学派的观点，只有“在区间内”、“在区间外”这两种情况，而不能讨论可能性(可能性是贝叶斯学派的观点)。

      通过以上的说明，可以获知这样一点内容：当误差线比较“长”时，一般要么是数据离散程度大，要么是数据样本少。

2.利用seaborn.barplot()绘制柱状图

     seaborn.barplot()绘图参数的说明为：

• x：指定label值，可以是一个序列
• y：对应每个label上的数据，可以是一个序列
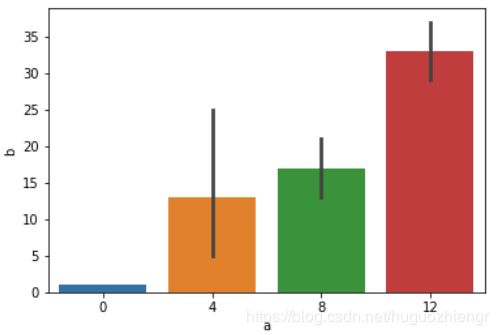
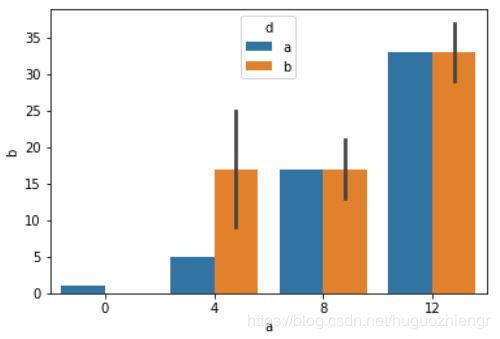
• hue：指定分类变量，其使用示例如下，左图是不使用hue参数时的图形，右图是使用hue的图形

>>> a=np.arange(40).reshape(10,4)
df=pd.DataFrame(a,columns=['a','b','c','d'])
df['a']=[0,4,4,8,8,8,4,12,12,12]
df['d']=list('aabbabbbab')
sns.barplot(x='a',y='b',data=df,hue='d')

                          

• data：使用的数据集。在上面的例子中，当指定"data=df"时，可以在“x=”、"y="处直接使用column名称，否则需要使用"x=data['a']"的形式
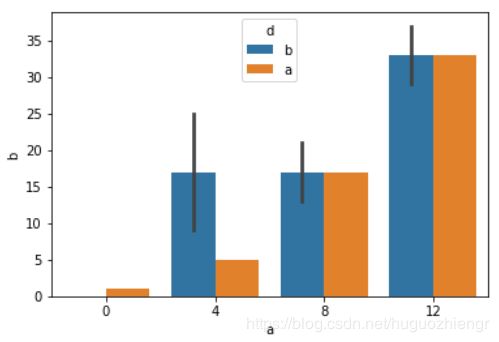
• order，hue_order：order控制bar绘制的顺序，hue_order控制一个bra内每个类绘图顺序，例如分别执行以下代码

>>> sns.barplot(x='a',y='b',data=df,order=[8,4,12,0])  #控制bar绘制顺序,左图
sns.barplot(x='a',y='b',data=df,hue_order=['b','a'])  #控制bar绘制顺序,右图

                         

• estimator：设置每一个label上显示的统计量类型,默认为平均值，可修改为最大值、中位值等。注意，若修改为非平均值，那么前面所提到的误差线都需要做修改，因为前面的误差线解释都是基于平均值的。
• ci：在seaborn.barplot()中误差线默认表示的是均值的置信区间，因此当ci为(0,100)间的值时表示置信区间的置信度，默认为95；ci还可以取值为'sd'，此时误差线表示的是标准误差；当ci取值为None时，则不显示误差线
• n_boot：计算代表置信区间的误差线时，默认会采用bootstrap抽样方法(在样本量较小时比较有用)，该参数控制bootstrap抽样的次数
• units：该参数的解释我暂时还未弄明白
• orient：设置柱状图水平绘制还是竖直绘制，"h"表示水平，“v”表示竖直。
• color：设置bar的颜色，这里似乎用于将所有的bar设置为同一种颜色
• pattle：调色板，设置bar的以不同颜色显示，所有的颜色选择都要是matplotlib是能识别的颜色
• saturation：设置颜色的饱和度取值为[0,1]间
• errcolor：设置误差线的颜色，默认为黑色
• errwidth：设置误差线的显示线宽
• capsize：设置误差线顶部、底端处横线的显示长度
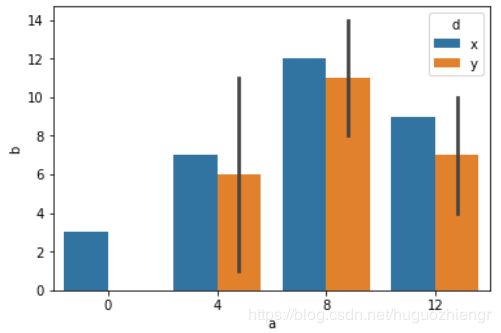
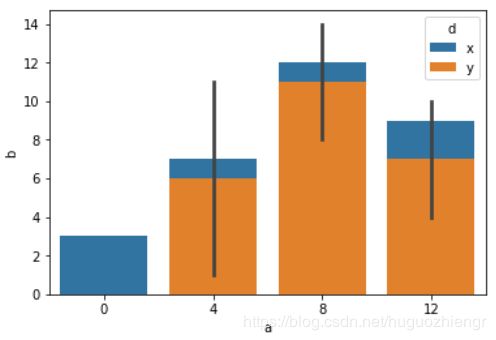
• dodge：当使用分类参数“hue”时，可以通过dodge参数设置是将不同的类分别用一个bar表示，还是在一个bar上通过不同颜色表示，下图总左边是dodge=True，右边是dodge=False，默认为True。

                        

• ax：选择将图形显示在哪个Axes对象上，默认为当前Axes对象
• kwargs：matplotlib.plot.bar()中其它的参数

 返回值:ax，matplotlib.Axes对象