拼多多2019.09.01秋招笔试 算法工程师 python 解法

 def pdd_1():
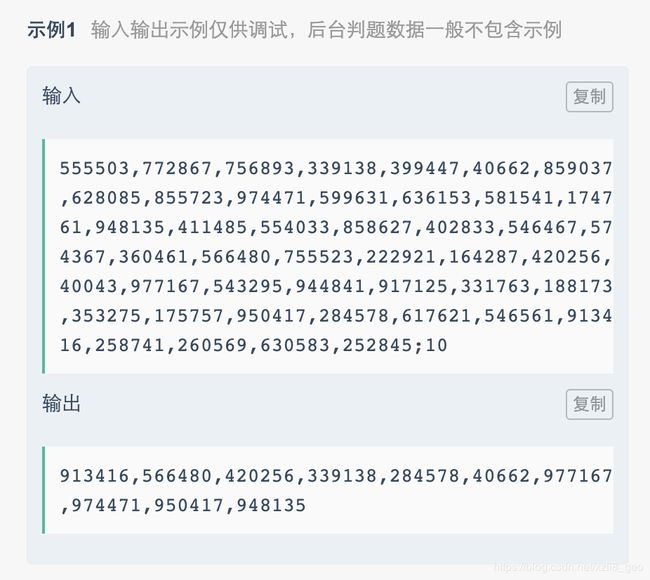
        # 根据取模运算，将奇数和偶数分开，分别排序，之后拼接输出
    
        # nums, N = input().split(';')
    
        aa = '555503,772867,756893,339138,399447,40662,859037,628085,855723,974471,599631,636153,581541,174761,948135,411485,554033,858627,402833,546467,574367,360461,566480,755523,222921,164287,420256,40043,977167,543295,944841,917125,331763,188173,353275,175757,950417,284578,617621,546561,913416,258741,260569,630583,252845;10'
        nums, N = aa.split(';')
        nums = map(int, nums.split(','))
        N = int(N)
    
        nums_0, nums_1 = [], []
        for i in nums:
            if i % 2 == 0:
                nums_0.append(i)
                nums_0.sort(reverse=True)
            else:
                nums_1.append(i)
                nums_1.sort(reverse=True)
    
        nums = nums_0 + nums_1
        for i in range(N - 1):
            print(nums[i], end=',')
        print(nums[N], end='')

  
  def pdd_2():
      # DFS 求解，着重找到递归结束的条件
      # DFS 注意顺序，以满足输出的字典序要求，避免二次排序
  
      def check(nums0, new_0, nums1, new_res):
          if not nums0:
              if len(new_0) == len(nums1):
                  for i in range(len(new_0)):
                      if new_0[i] != nums1[i]:
                          return
                  res.append(new_res)
              return
  
          num = nums0[0]
          nums0 = nums0[1:]
  
          check(nums0, new_0, nums1, new_res + ['d'])
          check(nums0, [num] + new_0, nums1, new_res + ['l'])
          check(nums0, new_0 + [num], nums1, new_res + ['r'])
  
      # N = int(input())
      N = 1
      for i in range(N):
          # nums_0 = list(map(int, input().split()))
          # nums_1 = list(map(int, input().split()))
  
          nums_0 = [1, 2, 3]
          nums_1 = [3]
          print('{')
          if set(nums_0) > set(nums_1):
              res = []
              check(nums_0, [], nums_1, [])
              for j in res:
                  print(' '.join(j))
          print('} ')

def pdd_3():
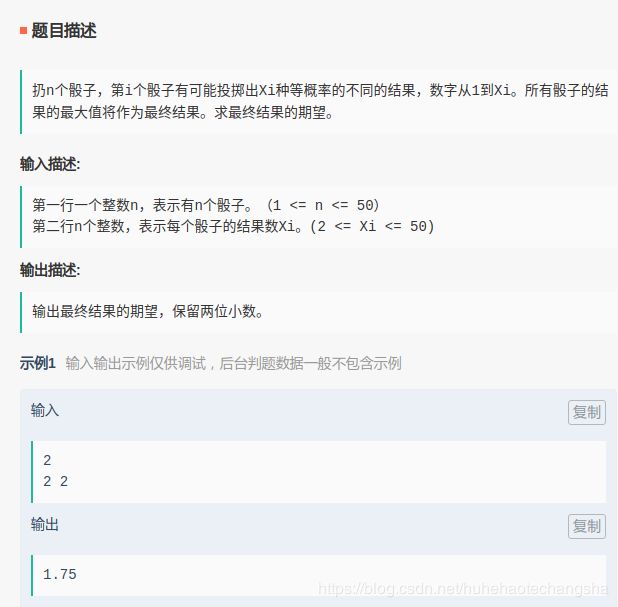
    # 寻找可能出现的最大结果，确定总共出现的结果数。
    # 确认每个可能出现结果的概率（需要减去前一个可能结果的概率）


    # N = int(input())
    # nums = list(map(int, input().split()))

    N = 5
    nums = [2, 2, 2, 9, 20]
    res = []
    front = 0
    for i in range(1, max(nums) + 1):
        tmp = 1.0
        for j in nums:
            tmp = tmp * (i / j if i < j else 1.0)
        res.append(tmp - front)
        front = tmp

    ans = 0.0
    for i in range(len(res)):
        ans += (i + 1) * res[i]

    print("%.2f" % ans)

``

def pdd_4():
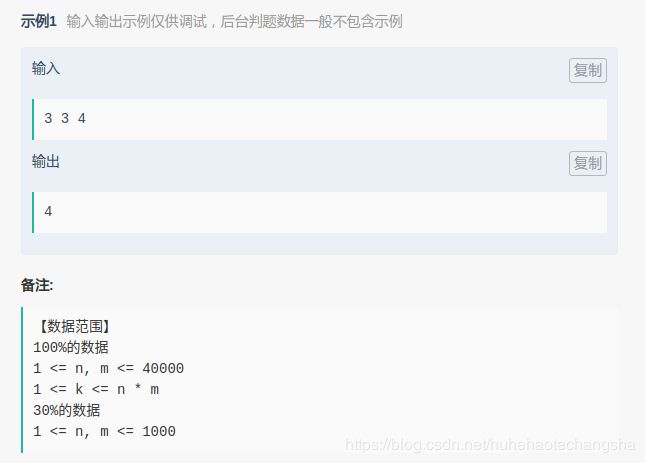
    # 寻找乘法表中第k大的数。

    # 暴力破解法  需要空间复杂度O(m*n) 时间复杂度O(m*n*(log(m*n)+1))
    # 二分法  空间复杂度O(1) 时间复杂度O(min(m,n)*log(m*n))

    # n, m, k = list(map(int, input().split()))
    n, m, k = 10, 10, 4

    l, r = 1, m * n
    if m > n:
        n, m = m, n
    k = m * n - k + 1
    while l < r:
        mid = l + (r - l) // 2
        count = 0
        for i in range(1, m + 1):
            count += min(mid // i, n)
        if count < k:
            l = mid + 1
        else:
            r = mid
    print(l)