人脸识别经典算法:Fisherface(LDA)
Fisherface是由Ronald Fisher发明的,想必这就是Fisherface名字由来。Fisherface所基于的LDA(Linear Discriminant Analysis,线性判别分析)理论和 特征脸 里用到的 PCA 有相似之处,都是对原有数据进行整体降维映射到低维空间的方法,LDA和PCA都是从数据整体入手而不同于LBP提取局部纹理特征.
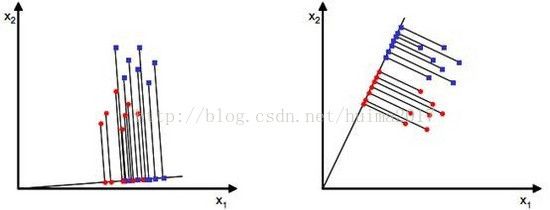
通常情况下,待匹配人脸要和人脸库内的多张人脸匹配,所以这是一个多分类的情况。出于简单考虑,可以先介绍二类的情况然后拓展到多类。假设有二维平面上的两个点集x(x是包含横纵坐标的二维向量),它们的分布如下图(1)(分别以蓝点和红点表示数据)
原有数据是散布在平面上的二维数据,如果想用一维的量(比如到圆点的距离)来合理的表示而且区分开这些数据,该怎么办呢?一种有效的方法是找到一个合适的向量w(和数据相同维数),将数据投影到w上(会得到一个标量,直观的理解就是投影点到坐标原点的距离),根据投影点来表示和区分原有数据。以数学公式给出投影点到到原点的距离: y=w T x。图(1)给出了两种w方案,w以从原点出发的直线来表示,直线上的点是原数据的投影点。直观判断右侧的w更好些,其上的投影点能够合理的区分原有的两个数据集。但是计算机不知道这些,所以必须要有确定的方法来计算这个w。
首先计算每类数据的均值(中心点):
这里的i是数据的分类个数,Ni代表某个分类下的数据点数,比如u1代表红点的中心,u2代表蓝点的中心。
数据点投影到w上的中心为:
如何判断向量w最佳呢,可以从两方面考虑:1、 不同的分类得到的投影点要尽量分开 ;2、同一个分类 投影后得到的点要尽量聚合 。从这两方面考虑,可以定义如下公式:
J(w)代表不同分类投影中心的距离,它的值越大越好。
上式称之为散列值(scatter matrixs),代表同一个分类投影后的散列值,也就是投影点的聚合度,它的值越小代表投影点越聚合。
结合两个公式,第一个公式做分子另一个做分母:
上式是w的函数,值越大w降维性能越好,所以下面的问题就是求解使上式取最大值的w。
把散列函数展开:
可以发现除w和w^T外,剩余部分可以定义为:
其实这就是原数据的散列矩阵了,对不对。对于固定的数据集来说,它的散列矩阵也是确定的。
另外定义:
S w 称为 Within -class scatter matrix。
回到 并用上面的两个定义做替换,得到:
展开J(w)的分子并定义 S B , S B 称为Between-class scatter。
这样就得到了J(w)的最终表示:
上式求极大值可以利用 拉格朗日乘数法 ,不过需要限定一下分母的值,否则分子分母都变,怎么确定最好的w呢。可以令 ,利用拉格朗日乘数法得到:
其中w是矩阵,所以求导时可以把 当做 。(这点我也不懂)
上式两边同乘以 可以得到:
可以发现w其实就是矩阵 的特征向量了对不对。
通过上式求解w还是有些困难的,而且w会有多个解,考虑下式:
将其带入下式:
其中 λ w 是以w为变量的数值,因为(u1-u2)^T和w是相同维数的,前者是行向量后者列向量。继续带入以前的公式:
由于w扩大缩小任何倍不影响结果,所以可以约去两遍的未知常数 λ 和 λ w (存疑):
到这里,w就能够比较简单的求解了。
2、数据集是多类的情况
假设有C个人的人脸图像,每个人可以有多张图像,所以按人来分,可以将图像分为C类,这节就是要解决如何判别这C个类的问题。判别之前需要先处理下图像,将每张图像按照逐行逐列的形式获取像素组成一个向量,和第一节类似设该向量为x,设向量维数为n,设x为列向量(n行1列)。
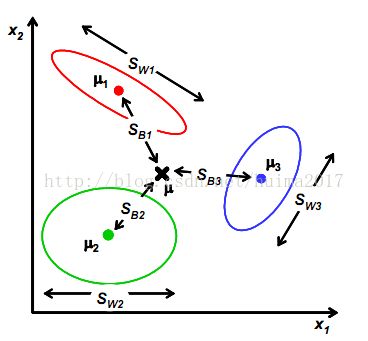
和第一节简单的二维数据分类不同,这里的n有可能成千上万,比如100x100的图像得到的向量为10000维,所以第一节里将x投影到一个向量的方法可能不适用了,比如下图:
图(2)
平面内找不到一个合适的向量,能够将所有的数据投影到这个向量而且不同类间合理的分开。所以我们需要增加投影向量w的个数(当然每个向量维数和数据是相同的,不然怎么投影呢),设w为:
w1、w2等是n维的列向量,所以w是个n行k列的矩阵,这里的k其实可以按照需要随意选取,只要能合理表征原数据就好。x在w上的投影可以表示为:
所以这里的y是k维的列向量。
像上一节一样,我们将从投影后的类间散列度和类内散列度来考虑最优的w,考虑图(2)中二维数据分为三个类别的情况。与第一节类似, μ i 依然代表类别i的中心,而 S w 定义如下:
其中:
代表类别i的类内散列度,它是一个nxn的矩阵。
所有x的中心 μ 定义为:
类间散列度定义和上一节有较大不同:
代表的是每个类别到 μ 距离的加和,注意Ni代表类别i内x的个数,也就是某个人的人脸图像个数。
上面的讨论都是投影之间的各种数据,而J(w)的计算实际是依靠投影之后数据分布的,所以有:
分别代表投影后的类别i的中心,所有数据的中心,类内散列矩阵,类间散列矩阵。与上节类似J(w)可以定义为:
回想我们上节的公式J(w),分子是两类中心距,分母是每个类自己的散列度。现在投影方向是多维了(好几条直线),分子需要做一些改变,我们不是求两两样本中心距之和(这个对描述类别间的分散程度没有用),而是求每类中心相对于全样本中心的散列度之和。得到:
最后化为:
还是求解矩阵的特征向量,然后根据需求取前k个特征值最大的特征向量。
另外还需注意:
由于S B 中的(μi-μ)秩为1,所以S B 的至多为C(矩阵的秩小于等于各个相加矩阵的和)。又因为知道了前C-1个μi后,最后一个μc可以用前面的μi来线性表示,因此S B 的秩至多为C-1,所以矩阵的特征向量个数至多为C-1。因为C是数据集的类别,所以假设有N个人的照片,那么至多可以取到N-1个特征向量来表征原数据。
PCA里求得的特征向量都是正交的,但是这里的 并不是对称的,所以求得的K个特征向量不一定正交,这是LDA和PCA最大的不同。
参考文献:
[1]Jerry Lead 线性判别分析(Linear Discriminant Analysis)(一)
[2]http://docs.opencv.org/modules/contrib/doc/facerec/facerec_tutorial.html