ROC与AUC
1、ROC、AUC概念介绍
2、ROC曲线绘制原理
3、ROC的曲线面积AUC
4、ROC曲线优点
1、ROC、AUC概念介绍
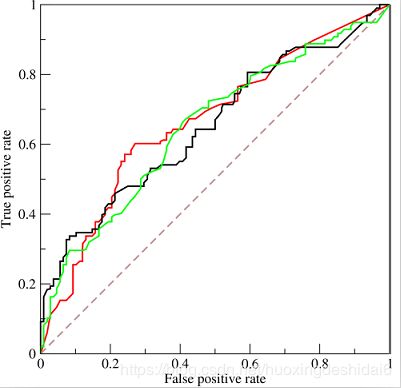
ROC的全名叫做Receiver Operating Characteristic，其主要分析工具是一个画在二维平面上的曲线——ROC curve。平面的横坐标是false positive rate(FPR)，纵坐标是true positive rate(TPR)。对某个分类器而言，我们可以根据其在测试样本上的表现得到一个TPR和FPR点对。这样，此分类器就可以映射成ROC平面上的一个点。调整这个分类器分类时候使用的阈值，我们就可以得到一个经过(0, 0)，(1, 1)的曲线，这就是此分类器的ROC曲线。一般情况下，这个曲线都应该处于(0, 0)和(1, 1)连线的上方。因为(0, 0)和(1, 1)连线形成的ROC曲线实际上代表的是一个随机分类器。
虽然，用ROC curve来表示分类器的performance很直观好用。可是，人们总是希望能有一个数值来标志分类器的好坏。于是Area Under roc Curve(AUC)就出现了。顾名思义，AUC的值就是处于ROC curve下方的那部分面积的大小。通常，AUC的值介于0.5到1.0之间，较大的AUC代表了较好的performance。
2、ROC曲线绘制原理
假如有一个样本集X，使用一个模型（逻辑回归或者SVM等）得出训练数据
，
...，
对应的权重
，
...，
以及
，则针对所有的
,
...,
（即为
，
...，
），有*W+b，*W+b...,，*W+b共m个值。
对于逻辑回归算法来说，将sigmod(*W+b)，sigmod(*W+b)...，sigmod(*W+b)的值从小到大排列，即可以得到m个threhold值（对应scikit-learn中的decision_function的值），设为
，
...，
（0
1）。默认情况下，逻辑回归将 sigmod(*W+b)>0.5 的时候，类别归为1，反之，类别归为0。
而ROC曲线则是通过调整区分类别的threhold值的界限得到不同的FPR和TPR的值，当界限为
的时候，sigmod(*W+b)> 的时候，类别归为1，反之，类别归为0。
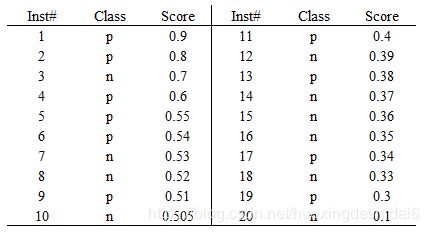
假如我们已经得到了所有样本的概率输出（属于正样本的概率），现在的问题是如何改变这个阈值（概率输出）？我们根据每个测试样本属于正样本的概率值从大到小排序。下图是一个示例，图中共有20个测试样本，“Class”一栏表示每个测试样本真正的标签（p表示正样本，n表示负样本），“Score”表示每个测试样本属于正样本的概率，即上文的sigmod(*W+b)的值。
接下来，我们从高到低，依次将“Score”值作为阈值，当测试样本属于正样本的概率大于或等于这个阈值时，我们认为它为正样本，否则为负样本。举例来说，对于图中的第4个样本（Inst# = 4），其“Score”值为0.6，那么样本1，2，3，4都被认为是正样本，因为它们的“Score”值都大于等于0.6，而其他样本则都认为是负样本。对应表格如下：
其中，因为"Score"大于等于0.6时，测试样本被预测为正样本，而实际正样本有3个（3个p，分别属于Inst#1,Inst#2,Inst#4），所以真实为正样本且被预测为正样本的数量为3，即[p,p]=3。同理，可以真实为负样本却被预测为正样本的数量为1（属于Inst#3），即[n,p]=1。可以得到FPR=1/(1+9)=0.1，TPR=3/(3+7)=0.3。所以，Score值为0.6的样本对应下图ROC曲线的坐标为（0.1,0.3）
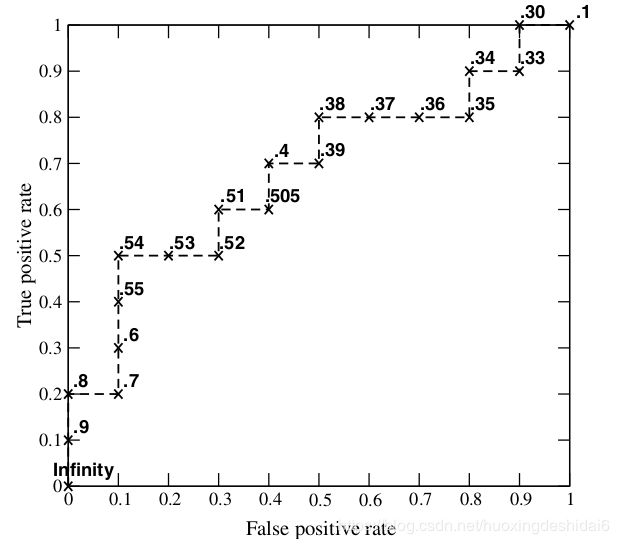
每次选取一个不同的阈值，我们就可以得到一组FPR和TPR，即ROC曲线上的一点。这样一来，我们一共得到了20组FPR和TPR的值，将它们画在ROC曲线的结果如下图：
当我们将阈值设置为1和0时，分别可以得到ROC曲线上的(0,0)和(1,1)两个点。将这些(FPR,TPR)对连接起来，就得到了ROC曲线。当阈值取值越多，ROC曲线越平滑。
3、ROC的曲线面积AUC
很多文献都会说,ROC曲线面积AUC值越大，则模型越好。这个乍一看，不太好理解，可以通过下面这个例子加深理解：
现在假设有一个训练好的二分类器对10个正负样本（原始样本中有正例5个，负例5个）预测，得分按高到低排序得到的最好预测结果为[1, 1, 1, 1, 1, 0, 0, 0, 0, 0]，即5个正例均排在5个负例前面，正例排在负例前面的概率为100%。然后绘制其ROC曲线，由于是10个样本，除开原点我们需要描10个点，如下： 
不难看出，上图的AUC等于1。此时，分类效果最好，即模型可以设定一个合适的threhold，在下图的1和0之间作为分类的界限，将样本100%分对。
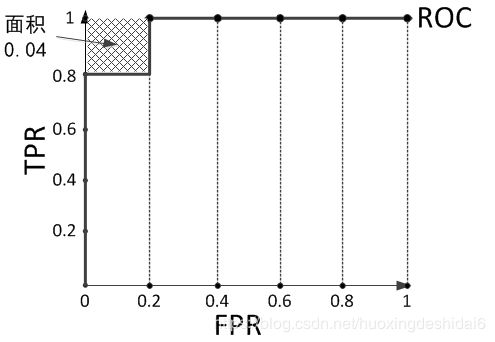
如果，又一个模型对这个10个样本预测，预测结果序列为[1, 1, 1, 1, 0, 1, 0, 0, 0, 0]，则对应ROC曲线如下图：
此时，AUC值小于1，无论设定何种threhold，都无法将样本完全正确分类，下图就有一个样本被错误分类：
不同的算法，同一算法不同参数，会导致样本集Score值不一样，这样在计算ROC曲线的时候，由于需要根据Score值进行排序，所以最终得到的ROC曲线不一样，AUC也不一样。AUC值越大，响应的模型越好。
4、ROC曲线优点
ROC曲线具有容忍样本倾斜的能力。ROC curves have an attractive property: they are insensitive to changes in class distribution. 看看公式TP/P 和FP/N本身就包含了归一化的思想（上面的表格每一行乘以常数C，TPR和FPR不变的），比如负样本*10的话 : FPR = (FP*10)/(N*10)，不变的。
再看看precision和recall就不行了，因为一个表格里是竖行，一个是横行。
precision=tp/(tp+fp), recall=tp/(tp+fn)
负样本*10的话 :
precision=tp/(tp+fp*10), recall=tp/(tp+fn)
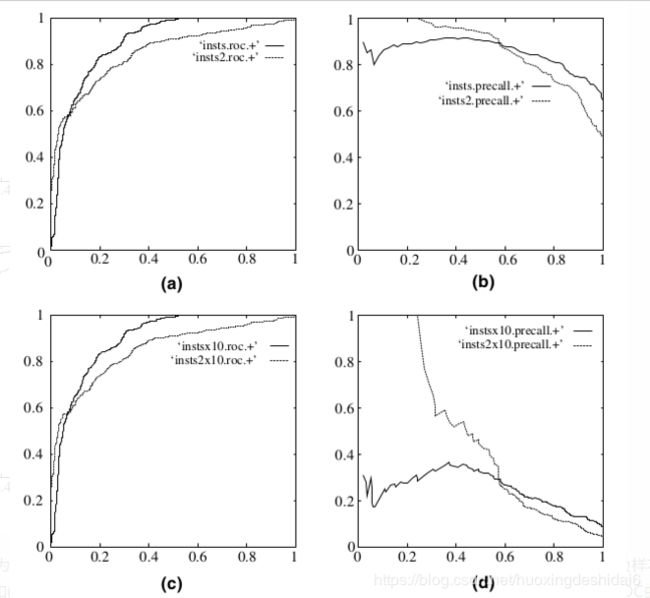
下图是ROC曲线和Precision-Recall曲线的对比：
在上图中，(a)和(c)为ROC曲线，(b)和(d)为Precision-Recall曲线。(a)和(b)展示的是分类其在原始测试集（正负样本分布平衡）的结果，(c)和(d)是将测试集中负样本的数量增加到原来的10倍后，分类器的结果。可以明显的看出，ROC曲线基本保持原貌，而Precision-Recall曲线则变化较大。
reference:
1、http://alexkong.net/2013/06/introduction-to-auc-and-roc/
2、http://blog.csdn.net/abcjennifer/article/details/7359370
3、https://blog.csdn.net/cherrylvlei/article/details/52958720