GLFW+OpenGL三维空间旋转模型的算法
在三维软件中,用鼠标控制三维模型旋转是很必要的,可以方便使用者观察模型,具有诸多优势,那么如何实现呢?
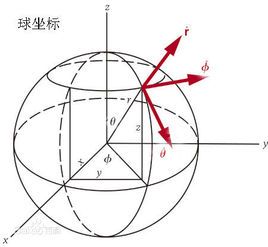
有两种方案,一种是控制模型旋转,这种方法将着色器中的model进行旋转变换即可;另一种是旋转摄像头,这种方法其实利用了相对运动的原理,要让模型旋转,其实也就是让观察者在以机器人模型为原点的球面坐标系中运动,当然运动之后,观察者也要旋转相应的角度。
这样一看是第一种方法简单,但是当模型位置不能动时(如要进行仿真,模型有确定的坐标),移动观察者变成唯一的选择。
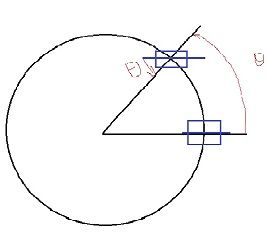
要实现旋转三维模型,第一步是定义一个鼠标的反馈函数,这个函数要将鼠标在屏幕中横向移动值转换为方位角,纵向移动值转换为天顶角,函数的调用需要按钮反馈函数以及鼠标移动函数的辅助。
按下鼠标右键的反馈:
void mouse_button_callback(GLFWwindow* window, int button, int action, int mods)
{
if (action == GLFW_PRESS) switch(button)
{
case GLFW_MOUSE_BUTTON_RIGHT:
glfwSetCursorPosCallback(window, mouse_callback2);
break;
default:
return;
}
if (action != GLFW_PRESS)
glfwSetCursorPosCallback(window, mouse_callback1);
return;
}
void mouse_callback2(GLFWwindow* window, double xpos, double ypos)
{
if (firstMouse)
{
lastX = xpos;
lastY = ypos;
firstMouse = false;
}
float xoffset = 0.1*(xpos - lastX);
float yoffset = 0.1*(lastY - ypos); // reversed since y-coordinates go from bottom to top
lastX = xpos;
lastY = ypos;
//camera.ProcessMouseMovement(xoffset, yoffset);
float r = sqrt(camera.Position.x * camera.Position.x + camera.Position.y * camera.Position.y + camera.Position.z * camera.Position.z);
float x,y,z,afa,fi;
if(camera.Position.x>=0)
{
afa = atan(camera.Position.z/camera.Position.x);
}
else
{
afa = atan(camera.Position.z/camera.Position.x)+3.1415926;
}
if(camera.Position.y>0)
{
fi = atan(camera.Position.x/(camera.Position.y*cos(afa)));
}
else
{
fi = atan(camera.Position.x/(camera.Position.y*cos(afa)))+3.1415926;
}
x = r*sin(fi+(yoffset)/180.0f*3.1415926)*cos(afa+(xoffset)/180.0f*3.1415926);
y = r*cos(fi+(yoffset)/180.0f*3.1415926);
z = r*sin(fi+(yoffset)/180.0f*3.1415926)*sin(afa+(xoffset)/180.0f*3.1415926);
camera.update(glm::vec3(x, y, z),glm::vec3(0.0f, 1.0f, 0.0f), -90.0f+afa/3.1415926*180.0+xoffset-83.6598f, 0.0f+fi/3.1415926*180.0+yoffset-69.7911f);
}
firstMouse提前设为true。
afa、fi是原始位置对应的方位角和天顶角,由于存在tan的反三角函数,需要讨论正负,并在值发生跳跃的时候补上180度,让选择连续。