GraphicsLab Project之基于物理的着色系统(Physical based shading) - 基于图像的光照(Image Based Lighting)（Diffuse篇）

作者：i_dovelemon
日期：2018-01-21
来源：CSDN
主题：PBR, Equrectangular Map, Cube Map, Irradiance Map, HDR Image, Pre-Filtering

引言

前面一篇文章讲述了怎么搭建一个PBS的直接光照系统。但是，想要发挥PBR的强大实力，就需要更加丰富的光照系统，本篇文章将要向大家展示，如何实现一个IBL-Diffuse的光照系统，实现的效果如下所示：

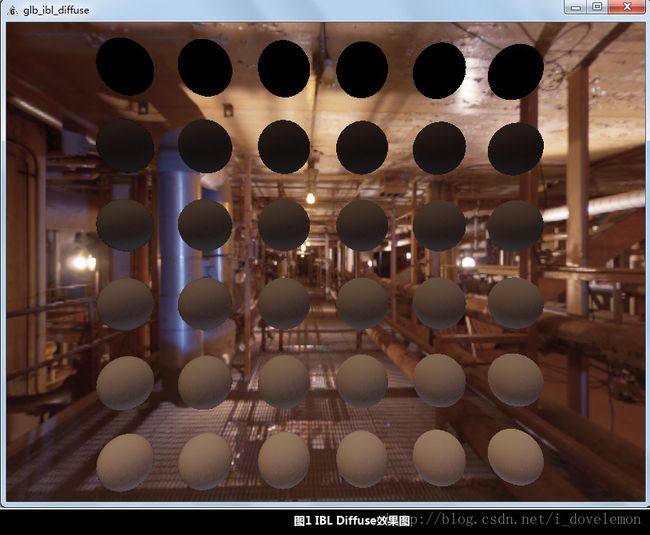
基于图像的光照(Image Based Lighting)

在开始之前，我们先来了解下什么是基于图像的光照(IBL)。一个物体，不会单独的存在一个空空的环境里面，它的周围一定有其他的物体。当光源照射到其他物体上的时候，一定也会反射，其中就有很多反射的光线会反射到该物体上去。上一篇文章中我们模拟的是直接光照。对于直接光照系统，像上面那种其他物体反射过来的光，我们一般就只是使用一个Ambient项来模拟。这种模拟方法只能够模拟单调的环境光照效果，想要更加丰富，更加精细的效果，我们就需要使用更加丰富的环境光照系统，而IBL就是实现它的一种方式。

一般来说，我们通过一张环境贴图(Environment Map)来保存一个物体周围的环境信息，然后通过某种处理，来实现丰富的环境光照效果。本文就是讲述，如何通过对环境贴图进行处理，然后实现丰富的环境光照效果。

从渲染方程解释IBL

还记得前面一篇文章中讲述的渲染方程嘛，这里再次的给出：

Lo=∫Ω(fd+fs)Li(pi,wi)n⋅widwi

根据前面对环境光照的描述，环境光照也应该符合这个公式，只不过相对于直接光照，它需要计算更多的入射光线。

同时从渲染方程可以看出，我们可以把渲染方程拆成两个部分进行处理：

Lo=∫ΩfdLin⋅widwi+∫ΩfsLin⋅widwi

本篇文章集中于处理：

Lo=∫ΩfdLin⋅widwi

对于这个方程，我们就可以将周围环境的所有光照信息保存在一张环境贴图中，而这个环境贴图就模拟了所有的 Li 。

环境贴图

在图形领域，用于保存周围环境信息的环境贴图有多种形式，如：

现在业界,对于IBL普遍使用的是Cube Map的形式。本篇文章也将主要使用Cube Map来进行IBL。

从前面一篇文章描述中我们知道，HDR对于PBR的重要性，没有了HDR，PBR的效果将大大折扣。所以，对于IBL来说，我们依然需要使用HDR。也就说，对于周围环境光照的描述，需要通过HDR的格式文件来保存。

本文的所有使用的环境光照贴图将从 sIBL中获取，这个网站里面有很多免费使用的HDR光照贴图，我们将从这些图中选择一些进行测试。

需要注意的是，这个网站里面的HDR贴图并不是CubeMap的形式，而是EquirectangularMap的形式进行保存的，所以接下来我们需要解决两个问题：如何读取.hdr文件，如何对这个贴图进行filter。

.hdr文件读取

在sIBL网站上，已经给出了.hdr文件格式的详细描述。我这里为了方便就直接使用了github上开源的stb_image库来读取.hdr文件。这个库里面都是一些单个文件的c代码库，感兴趣的读者可以自行探索。

使用它也很简单，只要简单的将stb_image.h包含到你的工程里面去，然后调用如下的代码：

stbi_set_flip_vertically_on_load(true);
int32_t width = 0, height = 0, component = 0;
float* data = stbi_loadf(file_name, &width, &height, &component, 0);
...
stbi_free(data);

你就能够得到.hdr文件保存的HDR数据了，然后可以通过图形API创建一个2D的HDR纹理，以便后续使用。

Equirectangular Map Filter

我们前面说过，我们将使用Cube Map来进行IBL。所以，我们需要一种方法来将该Equirectangular Map转换为Cube Map。为此，我们先简单的绘制一个球体，然后将这个Equirectangular Map贴上去，然后使用传统的创建Cube Map的方式产生一张Cube Map。

那么，我们怎么样将Equirectangular Map映射到球体上去了？通过一些简单的计算就能够完成这个操作，代码如下所示：

vec2 sampling_equirectangular_map(vec3 n) {
    float u = atan(n.z, n.x);
    u = (u + PI) / (2.0 * PI);

    float v = asin(n.y);
    v = (v * 2.0 + PI) / (2.0 * PI);

    return vec2(u, v);
}

上面代码中的n表示的是球体上某个点的法线，这个法线需要是归一化（normliaze）的。

通过计算atan(n.z, n.x)就能够得到具有该法线顶点的UV坐标的U值，通过计算asin(n.y)就能够得到具有该法线顶点的UV坐标的V值。同时，由于atan函数返回的结果在 [−π,π] 之间，而asin返回的结果在 [−π2,π2] 之间，所有需要把它们都映射到 [0,1] 之间。

下面是使用该方法得到的映射之后的结果：

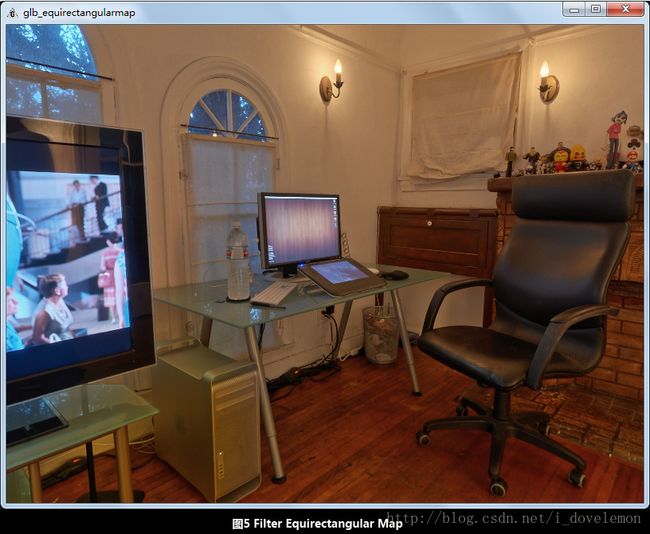
完整的代码可以在 glb_equirectangularmap中查看。

在得到了这个球体之后，我们就可以简单的使用传统的方法来创建CubeMap，主要就是通过设置FOV为90度的摄像机，分别朝着+X,-X,+Y,-Y,+Z,-Z去观察该球体，然后渲染CubeMap的6个面，从而得到一张HDR的CubeMap。该过程在 GraphicsLab Project之Dynamic Environment Mapping中详细的讲述了，这里就不在赘述。

预计算辐射光照贴图

简化积分方程

我们已经能够使用HDR的Cube Map来表示一个物体周围环境的光照信息了，接下来我们就需要计算渲染方程：

Lo=∫ΩfdLin⋅widwi

对于上面的渲染方程，我们需要求解一个积分运算。理论上，上面的渲染方程定义的积分域是半球空间，所以有无限个入射向量。对于这样的积分，我们没有办法硬解出来。所以在图形领域，一般采用概率和采样的方式来求解积分。常用的积分方法有：Monte Carlo积分，基于Monte Carlo积分改进的Importance Sampling积分，Riemann Sum等。本篇文章将要使用Riemann Sum的方式进行积分的求解，Importance Sampling的方法将在后续求Specular-IBL的时候详细介绍。

在进行实际积分运算之前，我们先来仔细的看下积分方程：

Lo=∫ΩfdLin⋅widwi

对于Diffuse部分的积分方程，我们知道如下的信息：

fd=kDcπ

也就是说，对于同一个点来说 fd 是一个常量，所以上述的方程可以简化为：

Lo=fd∫ΩLin⋅widwi

渲染方程球面坐标表示

为了方便进行积分运算，一般都将渲染方程改为球面坐标的积分形式，其中：

n⋅wi=cosθ

dwi=sinθdθdϕ

所以，方程转变为如下形式：

Lo=fd∫ϕ∫θLicosθsinθdθdϕ

关于 θ 和 ϕ 定义如下图所示：

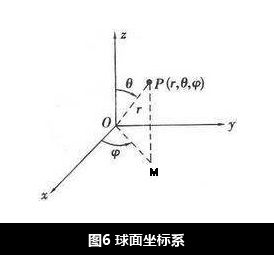
Riemann Sum(黎曼和)

Riemann Sum是一种很简单的积分方法，下面简要的介绍下。

我们假设有如下函数，值域在 [0,π] 上，

现在要求该函数与X轴所围图形的面积。对于这样一个不规则的图形，很难直接求出来它的面积，不过我们可以这样转换：肯定有一个长度为 π ，高度为h的矩形的面积，与该图形的面积一致，如下图所示：



所以，现在的问题，就变成了如何去求解这个h。理论上，这个h就应该等于所有在 [0,π] 定义域里面，函数 f(x) 值的平均值。

对于这个平均值的求法，Riemann Sum是这样来求解的：

设定一个步进值step，从函数的定义域 [0,π] 起点出发，一步一步的往终点去移动，计算每一个函数的值，然后将这些值求平均数（除以步进的步数），如下图所示：



这样，当我们的步进值越小的时候，通过这种方法计算出来的h值就越加的接近真实值。

所以上面的渲染方程的Riemann Sum形式变成如下：

Lo≈fd2πN1π2N2∑0N1∑0N2Licosθsinθ

其中：

fd=kDcπ

带入得到：

Lo≈kDcπ2πN1π2N2∑0N1∑0N2Licosθsinθ=kD∗c∗πN1N2∑0N1∑0N2Licosθsinθ

上述公式中，只有 kD 和 c 是未知的，我们不在积分里面计算，剩下的，都是能够通过预先计算得到。把这个过程转换为代码，如下所示：

float samplingStep = 0.025;
int sampler = 0;
vec3 l = vec3(0.0, 0.0, 0.0);
for (float phi = 0.0; phi < 2.0 * PI; phi = phi + samplingStep) {
    for (float theta = 0.0; theta < 0.5 * PI; theta = theta + samplingStep) {
        vec3 d = calc_cartesian(phi, theta);  // Transform spherical coordinate to cartesian coordinate
        d = d.x * r + d.y * u + d.z * n;  // Transform tangent space coordinate to world space coordinate
        l = l + filtering_cube_map(glb_CubeMap, normalize(d)) * cos(theta) * sin(theta);  // L * (ndotl) * sin(theta) d(theta)d(phi)
        sampler = sampler + 1;
        }
    }
    l = PI * l * (1.0 / sampler);
}

预计算操作

我们先仔细的观察下需要积分的渲染方程：

Lo=fd∫ΩLin⋅widwi

对于单个表面来说，这个积分方程里面，除了 fd 不需要考虑之外，积分里面的 n 也是固定不变的。所以，当我们最终将积分的结果保存在Cube Map里面，并且在实际渲染的时候，我们就是使用这个表面法线 n 来获取对应表面在半球积分里面的结果。所以，当我们在进行预计算的时候，其结果就需要与这样的获取方式相对应。也就说，对于CubeMap的6个面，我们分别使用其上的UV以及面的方向(+X,-X,+Y,-Y,+Z,-Z)来确定一个法线 n ，然后进行预计算。下面的代码，是根据面的方向以及UV确定一个法线 n 的代码：

vec3 calc_normal(int face, vec2 uv) {
    // 6 Face(+X,-X,+Y,-Y,+Z,-Z) for [0,5]
    uv = (uv - 0.5) * 2.0;  // Convert range [0, 1] to [-1, 1]

    vec3 n = vec3(0.0, 0.0, 0.0);
    if (face == 0) {
        // +X face
        n.x = 1.0;
        n.zy = uv;
    } else if (face == 1) {
        // -X face
        n.x = -1.0;
        n.z = -uv.x;
        n.y = uv.y;
    } else if (face == 2) {
        // +Y face
        n.y = 1.0;
        n.xz = uv;
    } else if (face == 3) {
        // -Y face
        n.y = -1.0;
        n.x = uv.x;
        n.z = -uv.y;
    } else if (face == 4) {
        // +Z face
        n.z = 1.0;
        n.x = -uv.x;
        n.y = uv.y;
    } else if (face == 5) {
        // -Z face
        n.z = -1.0;
        n.xy = uv;
    }

    return n;
}

对于Riemann Sum形式的积分方程：

Lo≈kD∗c∗πN1N2∑0N1∑0N2Licosθsinθ

其中只有 Li 是未知的了，所以我们需要根据 θ 和 ϕ 构造出这个 Li 出来。在每次运算过程中，我们通过步进得到了 θ 和 ϕ 值，不过这是球面坐标系的表示，我们得把它转换成为笛卡尔坐标，如下代码完成该操作：

vec3 calc_cartesian(float phi, float theta) {
    return vec3(sin(theta) * cos(phi), sin(theta) * sin(phi), cos(theta));
}

同时我们还需要知道一点，我们这里定义的 θ 和 ϕ 都是在 n 为(0,0,1)的空间中定义，所以我们需要将该向量转换到世界空间中去，如下代码：

// Calculate tangent space base vector
vec3 n = calc_normal(faceIndex, uv);
n = normalize(n);
vec3 u = vec3(0.0, 1.0, 0.0);
vec3 r = cross(u, n);
r = normalize(r);
u = cross(n, r);
u = normalize(u);
......

vec3 d = calc_cartesian(phi, theta);  // Transform spherical coordinate to cartesian coordinate
d = d.x * r + d.y * u + d.z * n;  // Transform tangent space coordinate to world space coordinate
l = filtering_cube_map(glb_CubeMap, normalize(d))

通过这样的方式，我们就能够得到积分方程里面 Li ，然后带入公式即可。

下面是完整的预计算代码：

#version 330
#extension GL_NV_shadow_samplers_cube : enable

in vec2 vs_TexCoord;

out vec3 oColor;

uniform samplerCube glb_CubeMap;
uniform int glb_FaceIndex;

const float PI = 3.1415926536898;

vec3 filtering_cube_map(samplerCube cube, vec3 n) {
    n.yz = -n.yz;
    return textureCube(cube, n).xyz;
}

vec3 calc_normal(int face, vec2 uv) {
    // 6 Face(+X,-X,+Y,-Y,+Z,-Z) for [0,5]
    uv = (uv - 0.5) * 2.0;  // Convert range [0, 1] to [-1, 1]

    vec3 n = vec3(0.0, 0.0, 0.0);
    if (face == 0) {
        // +X face
        n.x = 1.0;
        n.zy = uv;
    } else if (face == 1) {
        // -X face
        n.x = -1.0;
        n.z = -uv.x;
        n.y = uv.y;
    } else if (face == 2) {
        // +Y face
        n.y = 1.0;
        n.xz = uv;
    } else if (face == 3) {
        // -Y face
        n.y = -1.0;
        n.x = uv.x;
        n.z = -uv.y;
    } else if (face == 4) {
        // +Z face
        n.z = 1.0;
        n.x = -uv.x;
        n.y = uv.y;
    } else if (face == 5) {
        // -Z face
        n.z = -1.0;
        n.xy = uv;
    }

    return n;
}

vec3 calc_cartesian(float phi, float theta) {
    return vec3(sin(theta) * cos(phi), sin(theta) * sin(phi), cos(theta));
}

vec3 convolution_cube_map(samplerCube cube, int faceIndex, vec2 uv) {
    // Calculate tangent space base vector
    vec3 n = calc_normal(faceIndex, uv);
    n = normalize(n);
    vec3 u = vec3(0.0, 1.0, 0.0);
    vec3 r = cross(u, n);
    r = normalize(r);
    u = cross(n, r);
    u = normalize(u);

    // Convolution
    float samplingStep = 0.025;
    int sampler = 0;
    vec3 l = vec3(0.0, 0.0, 0.0);
    for (float phi = 0.0; phi < 2.0 * PI; phi = phi + samplingStep) {
        for (float theta = 0.0; theta < 0.5 * PI; theta = theta + samplingStep) {
            vec3 d = calc_cartesian(phi, theta);  // Transform spherical coordinate to cartesian coordinate
            d = d.x * r + d.y * u + d.z * n;  // Transform tangent space coordinate to world space coordinate
            l = l + filtering_cube_map(glb_CubeMap, normalize(d)) * cos(theta) * sin(theta);  // L * (ndotl) * sin(theta) d(theta)d(phi)
            sampler = sampler + 1;
        }
    }
    l = PI * l * (1.0 / sampler);

    return l;
}

void main() {
    vec3 color = convolution_cube_map(glb_CubeMap, glb_FaceIndex, vs_TexCoord);
    //oColor = color / (1.0 + color);
    oColor = color;
}

下图给出了预计算前后Cube Map的对比图：

需要注意，我这里预计算的Diffuse图尺寸在32×32。之所以选择较小的图，是因为Diffuse项是一个低频的信号，能够通过插值得到较好的结果，所以为了减少预计算的消耗，就选择了这个大小的尺寸。

IBL光照计算

有了前面的基础，这里的IBL光照计算就十分的简单，回顾下最后的渲染方程：

Lo≈kD∗c∗πN1N2∑0N1∑0N2Licosθsinθ

其中的：

πN1N2∑0N1∑0N2Licosθsinθ

已经通过预计算保存在了Cube Map里面，所以我们只要根据法线 n 获取Cube Map里面对应的值，然后乘上剩下的 kD∗c 就可以了。以下是完整的代码：

vec3 calc_ibl(vec3 n, vec3 v, vec3 albedo, float roughness, float metalic) {
    vec3 F0 = mix(vec3(0.04, 0.04, 0.04), albedo, metalic);
    vec3 F = calc_fresnel_roughness(n, v, F0, roughness);

    vec3 T = vec3(1.0, 1.0, 1.0) - F;
    vec3 kD = T * (1.0 - metalic);

    vec3 irradiance = filtering_cube_map(glb_IrradianceMap, n);

    return kD * albedo * irradiance;
}

需要额外说明的是，我们这里计算Fresnel系数的方式和前面直接光照系统的计算方式有所不同。这是因为对于IBL来说，我们没有办法得到一个单一的half向量，所以这里就直接使用了表面法线 n 来代替。但是这样就丢失了表面粗糙度的影响，所以重新设计了新的Fresnel函数，并且将roughness属性考虑进去。以下是考虑了roughness属性的新的Fresnel系数计算函数：

vec3 calc_fresnel_roughness(vec3 n, vec3 v, vec3 F0, float roughness) {
    float ndotv = max(dot(n, v), 0.0);
    return F0 + (max(vec3(1.0 - roughness), F0) - F0) * pow(1.0 - ndotv, 5.0);
}

总结

以上就是本篇文章的全部内容，配套代码放在：
https://github.com/idovelemon/GraphicsLabtory/tree/master/glbcodebase/graphicslab/glb_ibl_diffuse。

参考文献

[1]LearnOpenGL
[2]Article - Physically Based Rendering
[3]ScratchPixel
[4]Adapt a physically based rendering model