bp算法
又称反向传导算法,英文: back propagation。
我们了解,前向传导,可以根据W,b来计算出隐层、输出层的各个神经元的值以及对应的激活值,最终得到输出。如果输出和我们的目标存在误差,这个误差可以用成本函数表示(loss function),那么我们就需要反向的把这个误差分配到前面的各个传导的过程中,也就是W和B上;我们需要知道每个神经元带来了多少误差,这个影响程度我们用“残差”的概念来表示。
有了残差和目标函数,我们可以对参数W和B随机梯度下降法来求解,即:求导后表示为残差的某种共识。最后W的更新,与:残差、当前神经元的激活函数求导、输入值;由这三部分来共同决定参数的更新。如此反复迭代直到收敛。 从而求出W和B。
这个算法的核心则是:残差的求解;因为激活函数是事先定义的,输入值也是前向算法中已经计算好的。那么问题则归结为误差反向传导的时候,如何分配因子。
前向过程
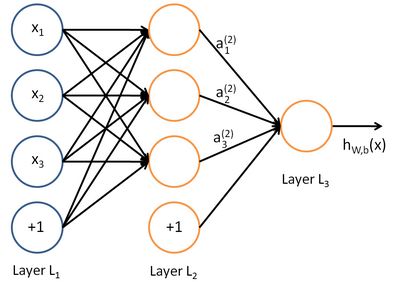
公式回顾和例子
a(2)1=f(W(1)11x1+W(1)12x2+W(1)13x3+b(1)1) a 1 ( 2 ) = f ( W 11 ( 1 ) x 1 + W 12 ( 1 ) x 2 + W 13 ( 1 ) x 3 + b 1 ( 1 ) )
这个是计算下一层第一个神经元的过程,就是利用前一层权重W和输入X线性组合后,加上偏置项,最后利用激活函数变换得到最终的结果。
这里需要澄清一下:
x1,x2,x3 x 1 , x 2 , x 3 代表的是三个特征值,而不是三个instance,这地方要清晰。 这一点在逻辑回归中更好理解,
X=[x1,x2,...,xn] X = [ x 1 , x 2 , . . . , x n ] 代表n个特征表示的一个样本数据,映射到
Y=+1,−1 Y = + 1 , − 1 (假设是二分类)。
而我们的第i个训练数据表示为
(X(i),y(i)) ( X ( i ) , y ( i ) ) .
例子
利用例子理解神经网络。
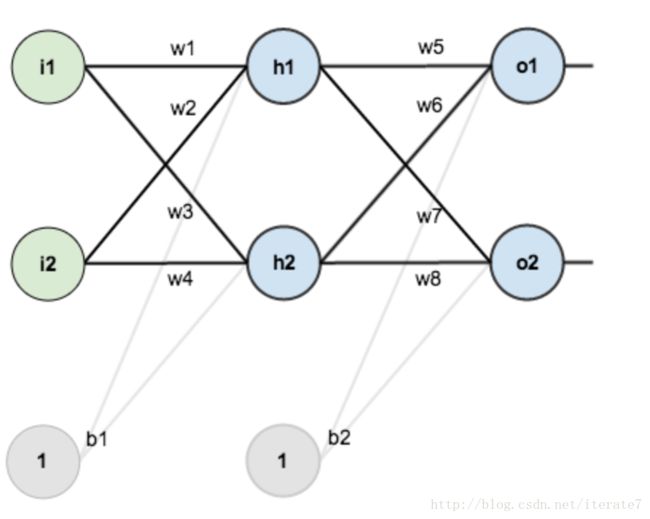
三层神经网络。
说明:
- 第一层是输入层,有2个神经元,i1和i2;截距项为b1=1;
- 第二层是隐含层,包括神经元h1,h2和截距项b2;
- 第三层是输出层o1,o2;
- 神经元之间的权重用w表示;
- 激活函数是sigmoid函数;
初始化
- 输入数据:i1=0.05, i2=0.10;
- 输出数据:o1=0.01, o2=0.99;
- 初始权重: w1=0.15, w2=0.20, w3=0.25, w4=0.30, w5=0.40, w6=0.45, w7=0.50, w8=0.55
目标:通过fp和bp算法,训练w和b,使得输入和输出匹配,拟合已有的数据。
step1:输入层到隐含层
神经元
neth1neth1=w1∗i1+w2∗i2+b1∗1=0.05∗0.15+0.10∗0.20+0.35∗1=0.3775(1)(2) (1) n e t h 1 = w 1 ∗ i 1 + w 2 ∗ i 2 + b 1 ∗ 1 (2) n e t h 1 = 0.05 ∗ 0.15 + 0.10 ∗ 0.20 + 0.35 ∗ 1 = 0.3775
注意net层只是线性组合,还没有执行激活函数;
outh1outh2=11+e−neth1=0.5932=0.5968(3)(4) (3) o u t h 1 = 1 1 + e − n e t h 1 = 0.5932 (4) o u t h 2 = 0.5968
这一步是执行激活操作。
参考:
each neuron is composed of two units. First unit adds products of weights coefficients and input signals. The second unit realise nonlinear function, called neuron activation function. Signal e is adder output signal, and y = f(e) is output signal of nonlinear element. Signal y is also output signal of neuron.
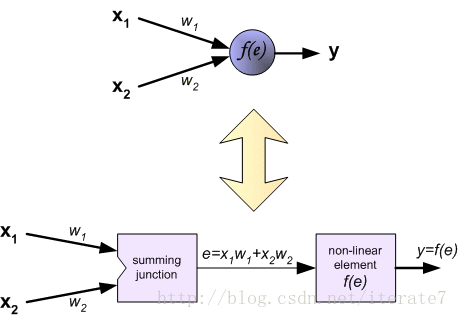
http://galaxy.agh.edu.pl/~vlsi/AI/backp_t_en/backprop.html (这篇后面的推导有问题,思路是对的。主要是负梯度有误,另外,一般用残差推导,这地方用的误差,残差=误差*激活求导。)
step2:隐含层到输出层
neto1neto1outo1outo2=w5∗outh1+w6∗outh2+b2∗1=0.4∗.0.5932+0.45∗.5968+0.6∗1=1.1=11+e−neto1=0.7513=0.7729(5)(6)(7)(8) (5) n e t o 1 = w 5 ∗ o u t h 1 + w 6 ∗ o u t h 2 + b 2 ∗ 1 (6) n e t o 1 = 0.4 ∗ .0 .5932 + 0.45 ∗ .5968 + 0.6 ∗ 1 = 1.1 (7) o u t o 1 = 1 1 + e − n e t o 1 = 0.7513 (8) o u t o 2 = 0.7729
这样前向传播的过程就结束了,我们得到输出值为【0.7513,0.7729】得到多少个输出取决于分类标签的维度,比如打算分成两个类,则为2;如果打算分成10个类,则有10个神经元。
与实际值【0.01,0.99】相差较大,开始计算误差,进行反向传播,更新权重,重新计算。
step3:计算误差
Etotal=∑12(target−output)2 E t o t a l = ∑ 1 2 ( t a r g e t − o u t p u t ) 2
有两个输出,误差分别计算o1和o2,总误差为两者之和:
Eo1=12(targeto1−outputo1)2=12(0.01−0.75)2=0.2748 E o 1 = 1 2 ( t a r g e t o 1 − o u t p u t o 1 ) 2 = 1 2 ( 0.01 − 0.75 ) 2 = 0.2748
Etotal=Eo1+Eo2=0.2748+0.0235=0.2984 E t o t a l = E o 1 + E o 2 = 0.2748 + 0.0235 = 0.2984
误差就是目标函数,也就是loss function。没有目标的优化都是耍流氓。
误差的传播
误差从哪里来,就用梯度转向那里去;为了找到源头,则要一步步的从后往前传递,所以才有了:反向传播;链式求导这两个概念。
针对我们的传播,大体上就是两个核心步骤:线性组合的求导;以及激活函数的求导。如此根据关联一步步相乘,这也是链式求导的内涵。见下图:
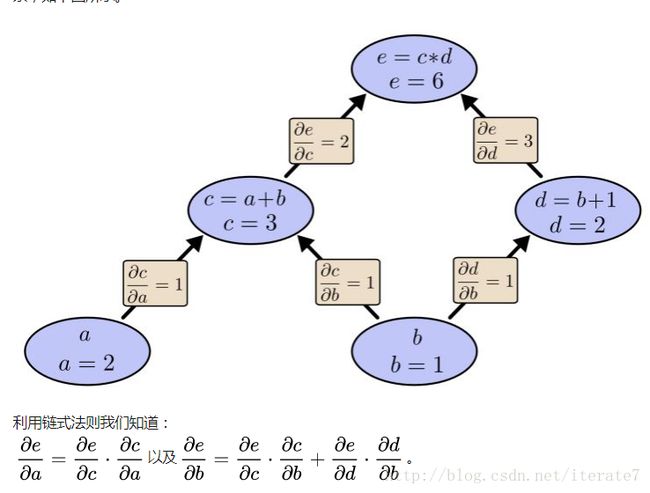
由于e和cd有关系;而cd又和ab有关系;于是梯度的链式法则如图所示。(从哪里来,到哪里去!)
针对我们的神经网络:
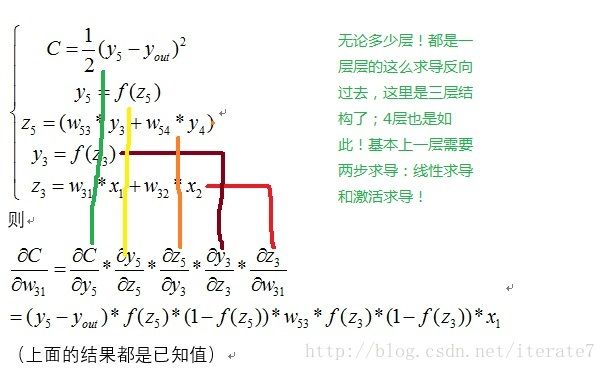
step4:输出层反向到隐含层
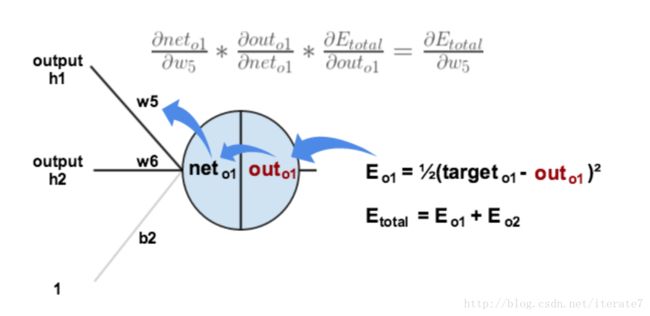
我们依照误差先输出节点求导、再激活函数求导、然后线性组合求导的原则可知:
∂Etotal∂w5=∂Etotal∂outo1⋅∂outo1∂neto1⋅∂neto1∂w5 ∂ E t o t a l ∂ w 5 = ∂ E t o t a l ∂ o u t o 1 ⋅ ∂ o u t o 1 ∂ n e t o 1 ⋅ ∂ n e t o 1 ∂ w 5
∂Etotal∂w5=∂Etotal∂outo1⋅∂outo1∂neto1⋅∂neto1∂w5=−(targeto1−outo1)⋅(outo1(1−outo1))⋅outh1=δo1⋅outh1=0.7413∗0.1868∗0.5932=0.0821(9)(10)(11)(12) (9) ∂ E t o t a l ∂ w 5 = ∂ E t o t a l ∂ o u t o 1 ⋅ ∂ o u t o 1 ∂ n e t o 1 ⋅ ∂ n e t o 1 ∂ w 5 (10) = − ( t a r g e t o 1 − o u t o 1 ) ⋅ ( o u t o 1 ( 1 − o u t o 1 ) ) ⋅ o u t h 1 (11) = δ o 1 ⋅ o u t h 1 (12) = 0.7413 ∗ 0.1868 ∗ 0.5932 = 0.0821
有了梯度,则用负梯度更新变量则可以保证目标函数下降最快。
w5:=w5−η∗∂Etotal∂w5=0.4−0.5∗0.0821=0.3589(13)(14)(15) (13) w 5 : = w 5 − η ∗ ∂ E t o t a l ∂ w 5 (14) = 0.4 − 0.5 ∗ 0.0821 (15) = 0.3589
w6w7w8=0.4086=0.5113=0.5614(16)(17)(18) (16) w 6 = 0.4086 (17) w 7 = 0.5113 (18) w 8 = 0.5614
step5:隐含层到隐含层
现在对w1求偏导;同理可以利用链式法则:
∂Etotal∂w1=∂Etotal∂outh1⋅∂outh1∂neth1⋅∂neth1∂w1(19) (19) ∂ E t o t a l ∂ w 1 = ∂ E t o t a l ∂ o u t h 1 ⋅ ∂ o u t h 1 ∂ n e t h 1 ⋅ ∂ n e t h 1 ∂ w 1
求导分三块,中间部分的求导是直接的,激活函数; 最后一部分求导也是线性求导,直接的。
第一部分则比较复杂一些,因为 outh1 o u t h 1 影响了o1和o2,所以反向求导的时候,则需要关联到 Eo1,Eo2 E o 1 , E o 2
那么我们就按照h1到最后的这条路径,一个个求导过来,并按照有多少路径累加,如果h1发出了3个神经元,则就需要反向三个梯度的累加。
∂Etotal∂w1=(∑o∂Etotal∂outo∂outo∂neto∂neto∂outh1)⋅∂outh1∂neth1⋅∂neth1∂w1(20) (20) ∂ E t o t a l ∂ w 1 = ( ∑ o ∂ E t o t a l ∂ o u t o ∂ o u t o ∂ n e t o ∂ n e t o ∂ o u t h 1 ) ⋅ ∂ o u t h 1 ∂ n e t h 1 ⋅ ∂ n e t h 1 ∂ w 1
正向的时候 w1->net(h1)->out(h1)->net(o1,o2,xxx)->out(o1,o2,xxx)->Etotal
反向求导的时候只要有关系,就必须求导相乘。
w1:=w1−η∗∂Etotal∂w1=0.1498(21)(22) (21) w 1 : = w 1 − η ∗ ∂ E t o t a l ∂ w 1 (22) = 0.1498
同理可求其他参数。
公式再归纳
从上面的示例中,我们大体了解了整个过程,那么我们再用公式推导一番。注意下面的公式将按照顺序直接给出,减少,防止思路中断。
(x(1),y(1)),…,(x(m),y(m))(1. m个样本) (1. m个样本) ( x ( 1 ) , y ( 1 ) ) , … , ( x ( m ) , y ( m ) )
J(W,b;x,y)=12||hW,b(x)−y||2(2. 损失函数) (2. 损失函数) J ( W , b ; x , y ) = 1 2 | | h W , b ( x ) − y | | 2
J(W,b)=1m∑J(W,b;x(i),y(i))=1m∑i12||hW,b(x(i))−y(i)||2(23)(3. 损失函数) (23) J ( W , b ) = 1 m ∑ J ( W , b ; x ( i ) , y ( i ) ) (3. 损失函数) = 1 m ∑ i 1 2 | | h W , b ( x ( i ) ) − y ( i ) | | 2
W(l)ijb(l)i=W(l)ij−α∂J(W,b)∂W(l)ij=b(l)i−α∂J(W,b)∂b(l)i(24)(4. 梯度公式) (24) W i j ( l ) = W i j ( l ) − α ∂ J ( W , b ) ∂ W i j ( l ) (4. 梯度公式) b i ( l ) = b i ( l ) − α ∂ J ( W , b ) ∂ b i ( l )
δ(l)i=∂J(W,b,x,y)∂zli(5. 残差定义) (5. 残差定义) δ i ( l ) = ∂ J ( W , b , x , y ) ∂ z i l
δ(nl)i=∂J(W,b,x,y)∂znli=∂12∑snlj=1(yj−f(znlj))2∂znli=(yi−f(znli))f′(znli)=(yi−anli)f′(znli)(25)(26)(27)(6. 输出层残差) (25) δ i ( n l ) = ∂ J ( W , b , x , y ) ∂ z i n l (26) = ∂ 1 2 ∑ j = 1 s n l ( y j − f ( z j n l ) ) 2 ∂ z i n l (27) = ( y i − f ( z i n l ) ) f ′ ( z i n l ) (6. 输出层残差) = ( y i − a i n l ) f ′ ( z i n l )
δ(l)i=(∑j=1sl+1Wljiδ(l+1)j)⋅f′(zli)(7. 其他层残差) (7. 其他层残差) δ i ( l ) = ( ∑ j = 1 s l + 1 W j i l δ j ( l + 1 ) ) ⋅ f ′ ( z i l )
从当前点传播过去的点都要反传回来,同时要对当前线性组合后的值求导,公式是激活函数。
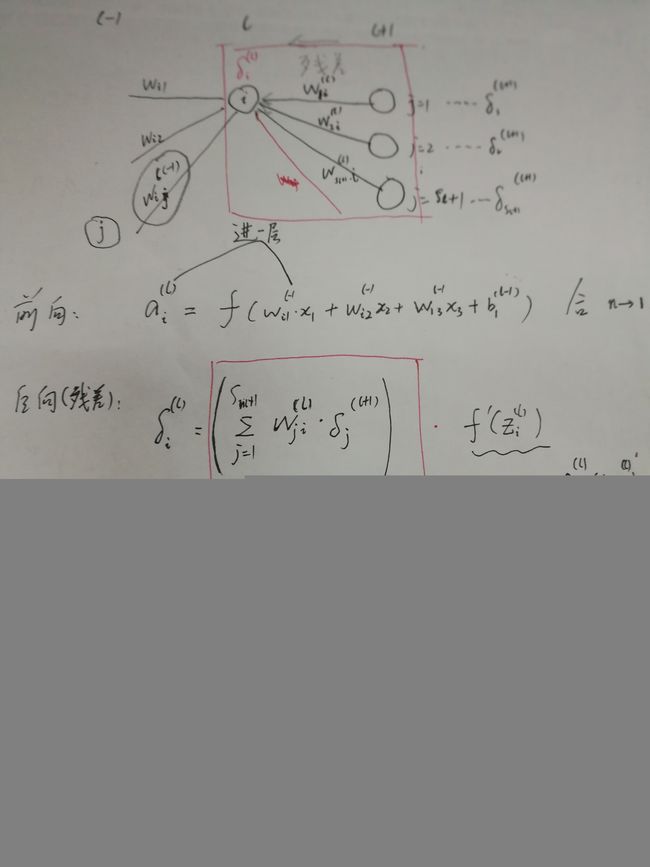
至此,梯度和残差的关系结束。
参考文献
http://ufldl.stanford.edu/wiki/index.php/%E5%8F%8D%E5%90%91%E4%BC%A0%E5%AF%BC%E7%AE%97%E6%B3%95
http://blog.csdn.net/zhaomengszu/article/details/77834845






