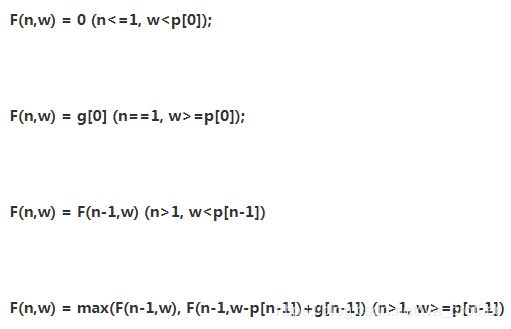动态规划:从入门到放弃
Dynamic programming is a method for solving a complex problem by breaking it down into a collection of simpler subproblems,solving each of those subproblems just once,and storing their solutions.
斐波拉契数列
由一个众所周知的例子入手,在学习C语言的时候,讲到递归的时候的经典例子,Fibonacci数列的求解。题目如下:
Fibonacci(n) = 1; n = 0
Fibonacci(n) = 1; n = 1
Fibonacci(n) = Fibonacci(n - 1) + Fibonacci(n - 2) 下面就是当时简单粗暴的解法,利用递归的方式。
int fib(int n)
{
if(n <= 0)
return 0;
if(n == 1)
return 1;
return fib(n - 1) + fib(n - 2);
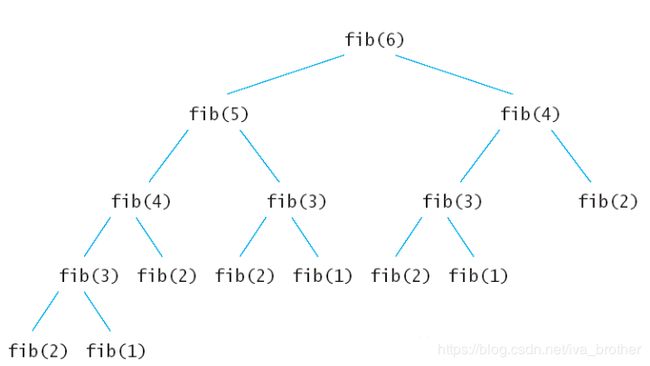
}下面看看算法的执行流程,假如输入6,那么执行的递归树如下所示。
上面的每个节点都会被执行一次,导致同样的节点被重复的执行,比如fib(2)被执行了5次。这样导致时间上的浪费,如果递归调用也会导致空间的浪费,导致栈溢出的问题。
下面说一个比较无聊的问题,什么是动态规划?动态规划和分治法看起来是非常像的思想,但是两者的区别也是非常明显的。分治法是将问题划分为互不相交的子问题,递归的求解子问题,再将它们的解组合起来,求出原问题的解。而动态规划是应用于子问题重叠的情况,即不同的子问题具有公共的子子问题。也就是上面Fibonacci的例子,上面的递归的求解方式就是分治算法,由于它的子问题是相互相关的,此时利用分治法就做了很多重复的工作,它会反复求解那些公共子子问题。而动态规划算法对每一个子子问题只求解一次,将其保存在一个表格中,从而避免重复计算。
下面我们介绍两种方法来说明动态规划的算法:自顶向下的备忘录法和自底向上的方法。
1、自顶而下的备忘录法
int Fibonacci(int n)
{
if(n <= 0)
return 0;
int meno[n + 1];
for(int i = 0; i <= n; i++)
meno[i] = -1;
return fib(n, meno);
}
int fib(int n, int *meno)
{
if(meno[n] != -1)
return meno[n];
if(n <= 2)
meno[n] = 1;
else
meno[n] = fib(n - 1, meno) + fib(n - 2, meno);
return meno[n];
}上述算法中,利用meno数组来存放斐波拉契数列中的每一个值,由于是自顶往下递归,它还是会最先递归到meno[3],从此刻开始在往上计算,然后依次保存计算结果在meno数组中,避免了重复运算。
下面是枯燥的概念,可以直接跳过。在动态规划当中包含三个重要的概念:最优子结构、边界、状态转移公式。对于上面这个算法来说,meno[10]的最优子结构就是fib(9,meno)和fib(8,meno)了;边界就是meno[2]与meno[1]了;状态转移方程就是meno[n] = fib(n - 1, meno) + fib(n - 2, meno)。注意最优子结构和状态转移方程的区别,个人理解是最优子结构是针对具体某个值来说的,而状态方程就是它的那个整体的推算方程。
2、自底而上的方法
自顶而下的方式来计算最终的结果,还是有一个递归的过程。既然最终是从fib(1)开始算,那么直接从fib(1)计算不就得了,先算子问题,再算父问题。
int fib(int n)
{
if(n <= 0)
return n;
int meno[n + 1];
meno[0] = 0
meno[1] = 1;
for(int i = 2; i <= n; i++)
meno[i] = meno[i - 1] + meno[i - 2];
return meno[n];
}我们从接触斐波拉契数列开始,就是递归的方式,弄到最后,发现还是直接来方便很多啊。但是该方法对于空间还是有一定的浪费,下面,我们对其空间再压缩一点。
int fib(int n)
{
if(n <= 1)
return n;
int meno_i_1 = 1;
int meno_i_2 = 0;
int meno_i = 1;
for(int i = 2; i <= n; i++)
{
meno_i = meno_i_1 + meno_i_2;
meno_i_2 = meno_i_1;
meno_i_1 = meno_i;
}
return meno_i;
}从上面的例子可以看到自顶向下的方式的动态规划其实包含了递归,而递归就会有额外的开销的;而使用自底向上的方式可以避免。看来斐波拉契真是个好东西,递归的时候用它来入门,现在动态规划也是用它来入门。
拓展例题:有一座n级台阶的楼梯,从下往上走,每跨一步只能向上1级或者2级台阶。要求用程序来求有多少种走法。(分析一下,其实就是斐波拉契数列!)
最长上升子序列
下面继续探讨动态规划的问题,继续一个栗子:求一个数列中最长上升子序列的长度(LIS,Longest Increasing Subsequence)的问题。
例如如下的一个数列:
它的最长上升子数列就是这样的了:
[1,2,3,4],长度为4,所以这个数列的最长上升子数列长度就是4。
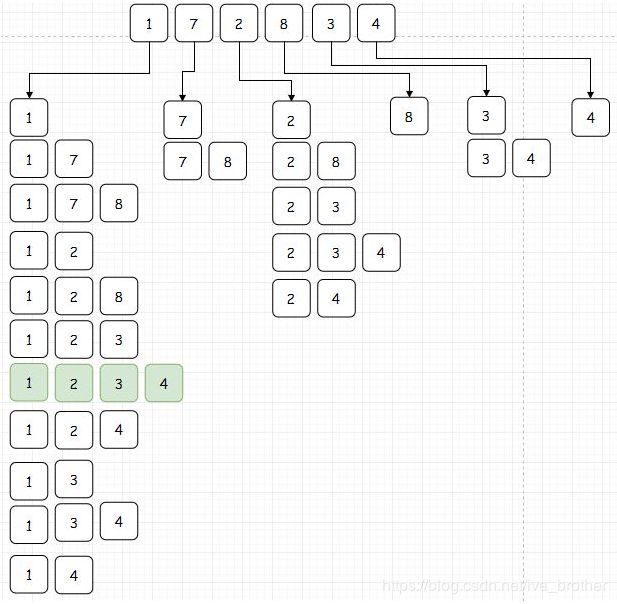
对于这个问题,最简单的求解方式就是暴力求解了,直接穷举。
直接这样找出所有的上升子序列,然后用肉眼观察哪个是最长的。显然,1,2,3,4是最长的,所以最长上升子序列的长度是4。
我们来看看这个方法的时间复杂度:
这就太消耗时间了。我们现在用动态规划试一下,看看有什么惊喜。
根据动态规划的定义,首先我们需要把原来的问题分解成了几个相似的子问题。但是,不同于斐波拉契数列的例子,这个如何分解原问题并不是那么一目了然。
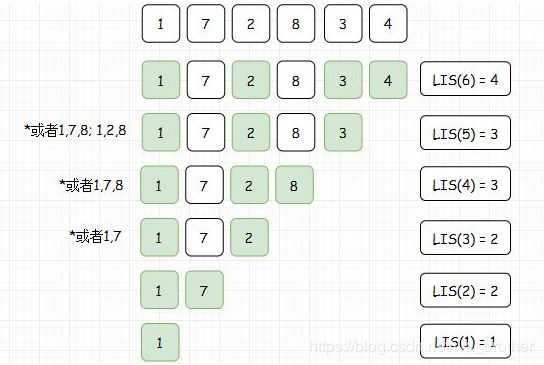
原来的问题是求LIS(n),现在我们需要找的就是LIS(n)和LIS(k)之间的关系1<=k<=n。如下所示:
这里我们可以看到,LIS(K+1)要么等于LIS(K),要么加了一。其实也很好理解,基本上就是,在前面所有的LIS种找到一个最长的LIS(i),如果A(K)比这个找到LIS(i)的尾项A(i)要大,则LIS(K)=LIS(i)+1,否则LIS(K)=LIS(i)。
这样的话,我们就分解了原问题,并且找到了原问题和子问题之间的关系:
i是对应的最大LIS(i)。也就是说,计算LIS(n)需要计算之前所有的LIS(K):
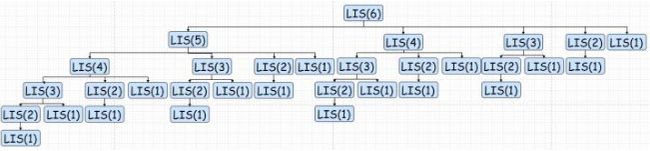
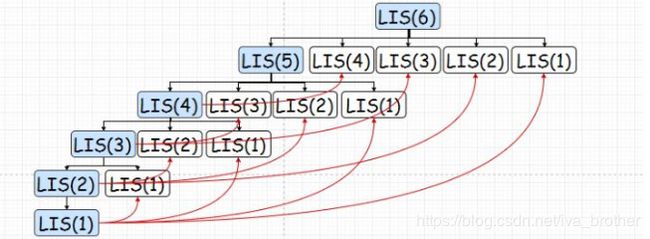
同理,我们可以储存子问题的结果,让每个子问题只被计算一次。需要计算的子问题就只剩下蓝色标出的部分了:
也就是(红色箭头表示调用了储存的数据,并未进行计算):
我们可以看到,采用了动态规划之后,时间复杂度大大降低了:纵轴方向的递归计算返回时间复杂度是O(n),横轴方向每行求Max的时间复杂度是O(logn),所以总共的时间复杂度就是O(nlogn),远远小于暴力穷举法的O(n!)。
下面是动态规划的代码:
int lis(int *arr, int n)
{
int dp[n];
memset(dp, 0, sizeof(dp));
int maxLen = 1;
for (int i = 0; i < n; ++i)
{
dp[i] = 1;
for (int j = 0; j < i; ++j)
{
if (a[i] > a[j] && dp[i] < (dp[j] + 1))
{
dp[i] = dp[j] + 1;
maxLen = ((maxLen > dp[i]) ? maxLen : dp[i]);
}
}
}
return maxLen;
}但是上面的这个方法的时间复杂度是O(n^2),并没有达到O(nlogn)。其中的dp[j](0 <= j <= i)来表示在i之前的LIS的长度,而dp[i]表示以i结尾的子序列中LIS的长度。在判断中加入 dp[i] < (dp[j] + 1)这个判断,来减少重复计算。
但是上面的讲解不是说有时间复杂度为O(nlogn)的算法的吗?有!利用二分法+动态规划就成了。代码如下:
int binarySearch(int *ans, int n,int left, int right)
{
while(left=arr[i])
right=mid;
else
left=mid+1;
}
return left;
}
int findLongest(int *arr, int n)
{
int ans[n];
ans[0] = arr[0];
int len=0;
for(i = 1; i < n; ++i){
if(arr[i]>ans[len])
ans[++len]=arr[i];
else{
int pos=binarySearch(i);
ans[pos] = arr[i];
}
}
return len + 1;
} 下面以一个数组举例来说明这种算法是怎么实现的?对于arr[9]={2,1,5,3,6,4,8,9,7}数组,我们来一步一步推理。
第一步:把arr[0]=2放入ans数组中,注意,这个ans数组用于存放最大上升子序列的元素,令ans[0]=2,此时len=1;
第二步:把arr[1]=1放入ans数组中,令ans[0]=1,也就是说长度为1的LIS的最小末尾是1,而ans[0]=2没有作用了,此时len=1;
第三步:arr[2]=5,arr[2]>ans[0],所以令ans[1]=arr[2]=5,此时len=2,也就是ans[2]={1,5},len=2;
第四步,arr[3]=3,它正好在1,5之间,放在1处肯定是不行的,因为1<3,长度为1的LIS最小末尾应该是1,长度为2的LIS最小末尾是3,于是可以把5淘汰掉,此时ans[2]={1,3},len=2;
第五步:arr[4]=6,它在3的后面,则可以将6放在3后面,此时ans[3]={1,3,6},len=3;
第六步:arr[5]=4,它在3与6,于是将6去掉,此时ans[3]={1,3,4},len=3;
第七步:arr[6]=8,它比4大,直接放在ans数组末尾,此时ans[4]={1,3,4,8},len=4;
第八步:arr[7]=9,它比8大,直接放在ans数组末尾,此时ans[4]={1,3,4,8,9},len=5;
第九步:arr[8]=7,它4、8之间,此时ans[4]={1,3,4,7,9},但是len不会更新,仍然是5。
特别提醒:这个1,3,4,7,9不是LIS字符串,本题中的LIS字符串应该是1,3,4,8,9。7代表的意思是存储5位长度LIS的最小末尾是7,所以在我们的ans数组,是储存对应长度LIS的最小末尾。有了这个末尾,我们就可以一个一个插入数据。例如这道题,如果这个arr数组7后面还有8、9,那么就可以继续的更新数据了,得到LIS的长度为6。
在插入数据的过程中,我们是替换而没有挪动数据,那么插入算法的话,就是二分查找来插入了,时间复杂度为O(nlogn)。
钢条切割
这是《算法导论》上面动态规划章节的例题,上面已经描述得非常清楚了,下面我们也是用三种方法来解这个问题。
递归版本
int cut(int *p,int n)
{
if(n==0)
return 0;
int q=0;
for(int i=1;i<=n;i++)
{
q = (q > (p[i-1]+cut(p, n-i)) ? q : (p[i-1]+cut(p, n-i)));
}
return q;
}这种自顶向下递归实现的效率会非常低,因为它会对相同的参数值进行递归调用,反复求解子问题。时间复杂度为O(2^n)。
备忘录版本
int cut(int*p,int n,int *r)
{
int q=-1;
if(r[n]>=0)
return r[n];
if(n==0)
q=0;
else {
for(int i = 1;i <= n; i++)
q=(q > cut(p, n-i,r)+p[i-1]) ? q : cut(p, n-i,r)+p[i-1] ;
}
r[n]=q;
return q;
}
int cutMeno(int *p, int n)
{
int r[n + 1];
for(int i = 0;i <= n;i++)
r[i] = -1;
return cut(p, n, r);
}自底向上的动态规划
int buttom_up_cut(int *p,int n)
{
int r[n + 1];
for(int i = 1;i <= n; i++)
{
int q=-1;
for(int j = 1;j <= i; j++)
q = (q> p[j-1]+r[i-j] ? q : p[j-1]+r[i-j]);
r[i] = q;
}
return r[n];
}自底向上的动态规划问题中最重要的是理解第二个for循环,这里外面的循环是求r[1],r[2]……,里面的循环是求出r[1],r[2]……的最优解,也就是说r[i]中保存的是钢条长度为i时划分的最优解,这里面涉及到了最优子结构问题,也就是一个问题取最优解的时候,它的子问题也一定要取得最优解。下面是长度为4的钢条划分的结构图。
国王与金矿
有一个国家发现了金矿,每座金矿的黄金储量不同,需要参与的人不同。参与挖矿的人为10人,每座金矿要么挖,要么不挖。每座金矿的黄金数与需要的人如下图所示,怎么样分配才能挖到最多的黄金呢?
对于每个金矿都有挖和不挖两种选择,所以问题的最优子结构有两个,例如现在有4个金矿挖,则剩余的人要么是10个,要么就是10个人减第5个需要的人。
我们令金矿数为n,工人数为w,金矿的黄金量为g[],金矿的用工量为p[]。有如下关系式。
int getMostGold(int n, int w, int* g, int* p)
{
if (n > g.length)
printf("输入的n值大于给定的金矿数\n");
if (w < 0)
printf("输入的工人数w不能为负数\n");
if (n < 1 || w == 0)
return 0;
int col = w+1; ////因为F(x,0)也要用到,所以表格应该有w+1列
int preResult[col];
int result[col];
//初始化第一行(边界)
for (int i = 0; i < col; i++) {
if (i < p[0])
preResult[i] = 0;
else
preResult[i] = g[0];
}
if (n == 1)
return preResult[w];
//用上一行推出下一行,外循环控制递推的轮数,内循环进行递推
for (int i = 1; i < n; i++) {
for (int j = 0; j < col; j++) {
if (j < p[i])
result[j] = preResult[j];
else
result[j] =(preResult[j]> preResult[j-p[i]] + g[i] ? preResult[j] :
preResult[j-p[i]] + g[i]);
}
for (int j = 0; j < col; j++) //更新上一行的值,为下一轮递推做准备
preResult[j] = result[j];
}
return result[w];
}该方法的时间复杂度为O(n*w),空间复杂度为O(w)。对于动态规划方法解法来说,当输入的矿山数多的时候,它的效率会非常高,但是当工人数多的时候,它的效率会低,而且低于简单的递归。
最后结尾,补充知乎关于动态规划问题的一个问答总结!
一个问题是该用递推、贪心、搜索还是动态规划,完全是由这个问题本身阶段间状态的转移方式决定的!
每个阶段只有一个状态->递推;
每个阶段的最优状态都是由上一个阶段的最优状态得到的->贪心;
每个阶段的最优状态是由之前所有阶段的状态的组合得到的->搜索;
每个阶段的最优状态可以从之前某个阶段的某个或某些状态直接得到而不管之前这个状态是如何得到的->动态规划。参考文档
https://blog.csdn.net/u013309870/article/details/75193592
https://www.zhihu.com/question/23995189
https://juejin.im/post/5a29d52cf265da43333e4da7
《算法导论》