求两个正整数的最大公约数Python版
求两个数的最大公约数我分别采用辗转相除法,辗转相减法,枚举法来求得。最小公倍数就是两个数之积除以最大公约数的结果。
(1)辗转相除法
思路:
1.将两整数求余 a%b = x
2.如果x = 0;则b为最大公约数
3.如果x != 0,则 a = b;b = x;继续从1开始执行
4.也就是说该循环的是否继续的判断条件就是x是否为0
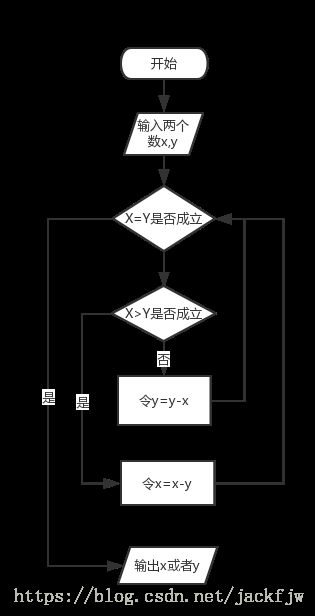
流程图
实现代码
#辗转相除法
def fun1(a,b):
x = a % b
while (x != 0):
a = b
b = x
x = a % b
return b(2)辗转相减法
思路:
1.如果a>b ,a = a - b;
2.如果b>a ,b = b - a;
3.假如a = b ,则 a或b 是最大公约数
4.如果a != b,则继续继续相减,直至a = b
流程图
实现代码
#辗转相减法
def fun2(a,b):
while a != b:
if a > b:
a = a - b
else:
b = b - a
return b(3)枚举法
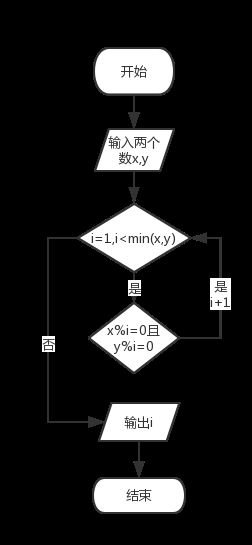
思路:
1.选出a,b中最小的一个数字放到min中
2.分别用a,b对i求余数,即看是否能被整除
3.直到a,b同时都能被i整除
4.如不能整除,i加一 继续开始执行,直到i等于min
流程图
实现代码
#枚举法
def fun3(a,b):
if a < b:
min = a
else:
min = b
i = 1
while i < min:
if a % i == 0:
if b % i == 0:
x = i
i += 1
return x