TensorFlow机器学习项目实战：简单的前向神经网络

 

神经网络是Tensorflow最擅长的机器学习领域。TensorFlow拥有一套符号引擎，它使得训练复杂模型变得更简单和方便。通过这套符号引擎，我们能够实现许多的模型结构和算法。

本文中，我们将会覆盖以下内容：

① 神经网络的基本概念；

② 神经网络用于回归非线性合成函数；

③ 使用非线性回归预测汽车燃料效率；

④ 学习葡萄酒分类——一种多类分类。

5.1.1　人工神经元

人工神经元就是使用一个数学函数来对生物的神经元建模。

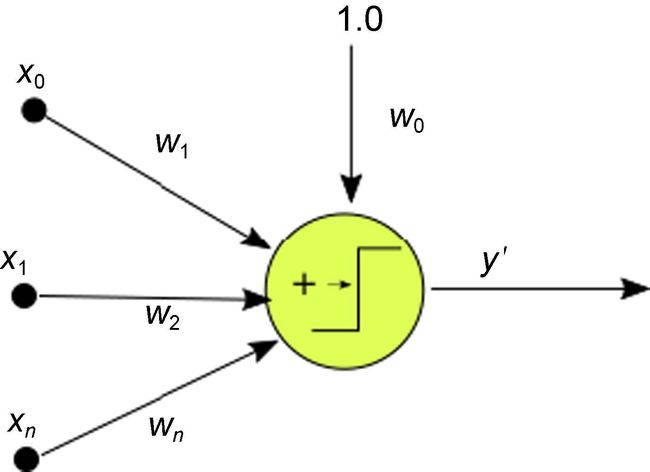
简单来说，一个人工神经元就是接受一个或者多个输入（训练数据），对它们加和，并产生一个输出。一般来说，这里面的加和指的是加权求和（每个输入乘上权重，并加上一个偏差），然后将加和的输入传递给一个非线性函数（一般称作激活函数或者转移函数）。

1．最简单的人工神经元——感知器

感知器是实现人工神经元最简单的方法，它的历史可以追溯到20世纪50年代，在20世纪60年代的时候，首次被实现。

简单来说，感知器就是一个二元分类函数，它将输入映射到一个二元输出，如图5-1所示。

图5-1　单层感知器

2．感知器算法

简化版的感知器算法如下：

① 以一个随机分布初始化权值和偏差（通常比较小）；

② 选择一个输入向量，并将其放入神经网络中；

③ 将输入与权重相乘，并加上偏差，计算网络的输出y'；

④ 感知器的函数如下：

⑤ 如果y′≠y，将权重wi加上Δw=yxi；

⑥ 返回第②步。

5.1.2　神经网络层

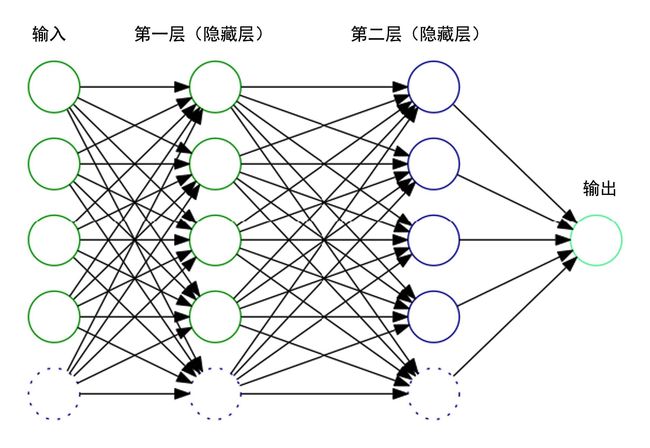
我们可以对单层的感知器进行泛华，将它们堆积起来，并互相连接，如图5-2所示。但这就带来一个问题，这样的线性组合出来的模型还只是一个线性分类器，对于复杂的非线性分类，这种方式并不能正确拟合，这个问题需要激活函数来解决。

1．神经网络激活函数

单独的单变量线性分类器并不能带来神经网络的强悍性能。就算那些不是很复杂的机器学习问题都会涉及多变量和非线性，所以我们常常要用其他的转移函数来替代感知器中原本的转移函数。

图5-2　连接单层感知器
 

有很多非线性函数可以用来做激活函数，从而表征不同的非线性模型。在输入同样的变量的时候，不同的激活函数有不同的响应。常用的激活函数如下：

• Logistic：典型的激活函数，在计算分类的概率时非常有用。

• Tanh：跟Sigmoid函数很像，但是范围是[−1,1]，而不是[0,1]。

• Relu：修正线性函数，该函数主要是为了对抗梯度消失。也就是当梯度反向传播到第一层的时候，梯度容易趋近于0或者一个极小值。

{-:-}f(x)=max(0, x)

在我们计算总的误差的时候，因为是一整个函数作用于输入数据，所以我们要调整这个方程中的所有变量，来最小化方程。

怎样最小化误差呢？正如我们在优化部分所学，我们通过损失函数的梯度来最小化误差。

如果我们的网络拥有多层权重和转移函数，我们最终需要通过链式法则来求导所有参数的梯度。

2．梯度和反向传播算法

在感知器的学习阶段，我们按照每个权重对误差的“责任”，按比例调整权重。

在更复杂的网络中，误差的责任被分散在整个结构的所有操作之中。

3．最小化损失函数：梯度下降

我们由图5-3理解一下损失函数。

4．神经网络的选择-分类vs回归

神经网络既可以被用于回归问题，也可以被用于分类问题。不同的地方在于结构的最后一层。如果需要的结果是一个数值，那么就不要连接标准函数，如 sigmoid。如果是这样的话，我们得到的就是一个连续值。

图5-3　梯度下降

5.1.3　有用的库和方法

本章中我们会用到TensorFlow中一些新的函数，下面是我们需要的最重要的函数：

1．TensorFlow激活函数

最常用的激活函数如下：

• tf.sigmoid(x)：标准的sigmoid函数；

• tf.tanh(x)：双曲正切函数；

• tf.nn.relu(x)：修正线性函数；

TensorFlow中其他的函数：

• tf.nn.elu(x)：指数线性单元；如果输入小于0，返回exp(x)−1；否则，返回x；

• tf.softsign(x)：返回x/(abs(x)+1)；

• tf.nn.bias_add(value,bias)：增加一个bias到value。

2．TensorFlow中损失优化方法

• tf.train.GradientDescentOptimizer(learningrate, uselocking, name)：原始梯度下降方法，唯一参数就是学习率。

• tf.train.AdagradOptimizer：自适应调整学习率，累加历史梯度的平方，作为分母，防止有些方向的梯度值过大，提高优化效率，善于处理稀疏梯度。

• tf.train.AdadeltaOptimizer：扩展AdaGrad优化方法，只累加最近的梯度值，而不对整个历史上的梯度值进行累加。

• tf.train.AdamOptimizertf.train.AdamOptimizer. (learningrate, beta1, beta2, epsilon, use locking, name)：梯度的一阶矩估计和二阶矩估计动态调整每个参数的学习率。Adam是自适应矩估计（Adaptive Moment Estimation）的首字母缩写。

3．Sklearn预处理函数

我们看一些下面的Sklearn数据预处理函数：

• preprocessing.StandardScaler()：数据正规化（Normalization）是机器学习估计的一个常见要求，为了模型能更好地收敛，我们通常会将数据集预处理到一个零均值单位方差的高斯状分布。通常，我们会将数据的各个维度都减去它的均值，然后乘上一个非零的数。这个非零的数就是数据集的标准差。对于该任务，我们直接使用StandardScaler，它已经实现了我们上面提到的操作。它也保留了变换操作，让我们可以直接用在测试集上。

• StandardScaler .fit_transform()：将数据调整到所需要的形式。StandardScaler对象会存储数据变化的变量，这样我们可以把数据解正规化到原先的格式。

• crossvalidation.traintest_split：该方法能够将数据集分割成训练集和测试集。我们只需要提供两者的比例，该方法能够自动帮我们处理。

5.2　例1——非线性模拟数据回归

人工神经网络的应用包含了很多的分类任务，但是事实上，很多这些分类任务都是用回归来实现的。

分类和回归的网络结构差的并不多，都可以使用多变量的输入，以及线性或者非线性的激活函数。

在一些例子中，唯一要变的就是在输出层，连接上Sigmoid状的函数，该函数能够表征结果为各个类别的可能性。

在第一个例子中，我们使用一个简单的带噪声的二次方程生成样本。模型我们使用带一个隐含层的神经网络，然后检测预测值跟真实值的距离远近。

5.2.1　数据集描述和加载

本例中，我们使用生成的数据集，这跟第3章线性回归类似。

我们这次选择的方程是一个二次方程，并加上随机噪声，这有助于帮助我们测试回归的泛化能力。

核心代码如下：

import numpy as np trainsamples = 200 testsamples = 60 dsX = np.linspace(-1, 1, trainsamples + testsamples).transpose() dsY = 0.4* pow(dsX,2) +2 * dsX + np.random.randn(*dsX.shape) * 0.22 + 0.8 

5.2.2　数据集预处理

本例中的数据集不需要预处理，因为它是我们人工生成的，具有更好的性能，比如能够保证数据范围是(−1,1)。

5.2.3　模型结构——损失函数描述

本例中的损失函数使用均方误差，由以下代码实现：

cost = tf.pow(py_x-Y, 2)/( 2) 

5.2.4　损失函数优化器

本例中，我们使用梯度下降作为损失函数优化器，可以用以下代码实现：

train_op = tf.train.AdamOptimizer( 0.5).minimize(cost) 

5.2.5　准确度和收敛测试 predict_op = tf.argmax(py_x, 1) cost1 += sess.run(cost, feed_dict={X: [[x1]], Y: y1}) / testsamples 

5.2.6　完整源代码

完整源代码如下：

import tensorflow as tf import numpy as np from sklearn.utils import shuffle %matplotlib inline import matplotlib.pyplot as plt trainsamples = 200 testsamples = 60 #Here we will represent the model, a simple imput, a hidden layer of sigmoid activation def model(X, hidden_weights1, hidden_bias1, ow): hidden_layer = tf.nn.sigmoid(tf.matmul(X, hidden_weights1)+ b) return tf.matmul(hidden_layer, ow) dsX = np.linspace(-1, 1, trainsamples + testsamples).transpose() dsY = 0.4* pow(dsX,2) +2 * dsX + np.random.randn(*dsX.shape) * 0.22 + 0.8 plt.figure() # Create a new figure plt.title('Original data') plt.scatter(dsX,dsY) #Plot a scatter draw of the datapoints X = tf.placeholder( "float") Y = tf.placeholder( "float") # Create first hidden layer hw1 = tf.Variable(tf.random_normal([1, 10], stddev=0.1)) # Create output connection ow = tf.Variable(tf.random_normal([10, 1], stddev=0.0)) # Create bias b = tf.Variable(tf.random_normal([10], stddev=0.1)) model_y = model(X, hw1, b, ow) # Cost function cost = tf.pow(model_y-Y, 2)/(2) # construct an optimizer train_op = tf.train.GradientDescentOptimizer(0.05).minimize(cost) # Launch the graph in a session with tf.Session() as sess: tf.initialize_all_variables().run() #Initialize all variables for i in range(1,100): dsX, dsY = shuffle (dsX.transpose(), dsY) #We randomize the samples to mplement a better training trainX, trainY =dsX[0:trainsamples], dsY[0:trainsamples] for x1,y1 in zip (trainX, trainY): sess.run(train_op, feed_dict={X: [[x1]], Y: y1}) testX, testY = dsX[trainsamples:trainsamples + testsamples], dsY[0:trainsamples:trainsamples+testsamples] cost1=0. for x1,y1 in zip (testX, testY): cost1 += sess.run(cost, feed_dict={X: [[x1]], Y: y1}) / testsamples if (i%10 == 0): print "Average cost for epoch " + str (i) + ":" + str(cost1) 

5.2.7　结果描述

生成的人工数据的散点图如图5-4所示。

图5-4　人工数据散点图

由以下每次迭代的结果，我们知道该实现结果非常好，甚至在第一次迭代的时候就取得了不错的结果。

Average cost for epoch 1:[[ 0.00753353]] Average cost for epoch 2:[[ 0.00381996]] Average cost for epoch 3:[[ 0.00134867]] Average cost for epoch 4:[[ 0.01020064]] Average cost for epoch 5:[[ 0.00240157]] Average cost for epoch 6:[[ 0.01248318]] Average cost for epoch 7:[[ 0.05143405]] Average cost for epoch 8:[[ 0.00621457]] Average cost for epoch 9:[[ 0.0007379]] 

5.3　例2——通过非线性回归，对汽车燃料效率建模

本例中，我们会进入一个新的领域：解决非线性问题。该领域是神经网络附加值最大的领域。开始该旅程之前，我们会对几个汽车型号的燃料效率建模。该问题的输入是多个变量，只有非线性模型才能取得比较好的结果。

5.3.1　数据集描述和加载

对该问题，我们会分析一个著名的、标准的、数据组织得很好的数据集。我们有一个多变量的输入（有连续的，也有离散的），预测每加仑英里数（mpg）。

这是一个玩具级例子，但是这个例子会铺开通往更复杂问题的道路。而且该例子还有个好处，就是被大量研究过。

数据集由如下的列组成。

• mpg：每加仑英里数，连续。

• cylinders：气缸，多值离散。

• displacement：排量，连续。

• horsepower：马力，连续。

• weight：车重，连续。

• acceleration：加速度，连续。

• model year：年份，多值离散。

• origin：产地，多值离散。

• car name：车名，字符串（不会被使用）。

我们不会对该数据做详细的分析，我们只是想看一下每一个连续的变量都跟目标变量的增减相关，如图5-5所示。

图5-5　不同的变量和燃烧效率的关系散点图

5.3.2　数据预处理

本例中，我们会使用一个前面描述的sklearn中的StandardScaler对象：

• scaler = preprocessing.StandardScaler()

• Xtrain = scaler.fittransform(X_train)

5.3.3　模型架构

我们需要建立的是一个多变量输入，单变量输出的前向神经网络，如图5-6所示。

图5-6　模型架构

5.3.4　准确度测试

我们用以下代码实现准确度测试：

score = metrics.mean_squared_error(regressor.predict(scaler.transform(X_test)), y_test) print( " Total Mean Squared Error: " + str(score)) 

5.3.5　结果描述 Step #99, avg. trainloss: 182 .33624 Step #199, avg. train loss: 25 .09151 Step #300, epoch #1, avg. trainloss: 11 .92343 Step #400, epoch #1, avg. train loss: 11 .20414 Step #500, epoch #1, avg. train loss: 5 .14056 Total Mean Squared Error: 15 .0792258911 

5.3.6　完整源代码

完整源代码如下：

%matplotlib inline import matplotlib.pyplot as plt import pandas as pd from sklearn import datasets, cross_validation, metrics from sklearn import preprocessing from tensorflow.contrib import skflow # Read the original dataset df = pd.read_csv( "data/mpg.csv", header=0) # Convert the displacement column as float df['displacement']=df['displacement'].astype(float) # We get data columns from the dataset# First and last (mpg and car names) are ignored for X X = df[df.columns[1:8]] y = df['mpg'] plt.figure() # Create a new figure for i in range (1,8): number = 420 + i ax1.locator_params(nbins=3) ax1 = plt.subplot(number) plt.title(list(df)[i]) ax1.scatter(df[df.columns[i]],y) #Plot a scatter draw of the datapoints plt.tight_layout(pad=0.4, w_pad=0.5, h_pad=1.0) # Split the datasets X_train, X_test, y_train, y_test = cross_validation.train_test_split(X, y, test_size=0.25) # Scale the data for convergency optimization scaler = preprocessing.StandardScaler() # Set the transform parameters X_train = scaler.fit_transform(X_train) # Build a 2 layer fully connected DNN with 10 and 5 units respectively regressor = skflow.TensorFlowDNNRegressor(hidden_units=[10, 5], steps=500, learning_rate=0.051, batch_size=1) # Fit the regressor regressor.fit(X_train, y_train) # Get some metrics based on the X and Y test data score = metrics.mean_squared_error(regressor.predict(scaler.transform(X_test)), y_test) print( " Total Mean Squared Error: " + str(score)) 

5.4　例3——多类分类：葡萄酒分类

本部分，我们会处理一个更复杂的数据集，预测葡萄酒的原产地。

5.4.1　数据集描述和加载

这个数据集包含了3种不同起源的葡萄酒，每个数据有13个属性。这些葡萄酒都由意大利制造，但是原产地不一样。

数据变量：

• Alcohol：酒精度。

• Malic acid：苹果酸。

• Ash：灰。

• Alcalinity of ash：灰分的碱度。

• Magnesium：镁含量。

• Total phenols：总酚类。

• Flavanoids：黄烷类。

• Nonflavanoid phenols：非类黄烷酚。

• Proanthocyanins：原花青素。

• Color intensity：颜色强度。

• Hue：色相。

• OD280/OD315 of diluted wines：稀释葡萄酒的OD280 / OD315。

• Proline：脯氨酸。

读取该数据集，我们只需要调用pandas库即可。

df = pd.read_csv( "./wine.csv", header= 0) 5.4.2　数据集预处理

因为该csv文件从1开始，为数据减去该偏差：

y = df[ 'Wine'].values- 1

对于其结果，我们使用一位有效编码：

Y = tf.one_hot(indices = y, depth=3, on_value = 1., off_value = 0., axis = 1 , name = "a").eval()

不同变量跟原产地关系散点图如图5-7所示。同样，我们会选择预先打乱数据：

图5-7　不同变量跟原产地关系散点图

X, Y = shuffle (X, Y) scaler = preprocessing.StandardScaler() X = scaler.fit_transform(X) 5.4.3　模型架构

该模型只需要一个单层的全链接神经网络：

• x = tf.placeholder(tf.float32, [None, 12])。

• W = tf.Variable(tf.zeros([12, 3]))。

• b = tf.Variable(tf.zeros([3]))。

• y = tf.nn.softmax(tf.matmul(x, W) + b)。

5.4.4　损失函数描述

我们选择交叉熵作为损失函数：

y_ = tf.placeholder(tf.float32, [None, 3]) cross_entropy = tf.reduce_mean(-tf.reduce_sum(y_ * tf.log(y), reduction_indices=[ 1])) 5.4.5　损失函数优化器

我们又一次选择梯度下降作为损失函数的优化器。

train_step = tf.train.GradientDescentOptimizer( 0.1).minimize(cross_entropy) 5.4.6　收敛性测试

在收敛性测试中，我们将正确预测的结果算作1，错误预测的结果算作0，计算它们的均值，作为该模型的准确度。

correct_prediction = tf.equal(tf.argmax(y, 1), tf.argmax(y_, 1)) accuracy = tf.reduce_mean(tf.cast(correct_prediction, tf.float32)) print(accuracy.eval({x: Xt, y_: Yt}))5.4.7　结果描述

正如我们所见，准确度会随着迭代的次数而波动，但一直是一个大于90%的准确率，远高于30%的基准线（如果我们随机猜测一个0～3的结果）。

0 .973684 0 .921053 0 .921053 0 .947368 0 .921053 5.4.8　完整源代码

完整源代码如下：

sess = tf.InteractiveSession() import pandas as pd # Import data from tensorflow.examples.tlutorials.mnist import input_data from sklearn.utils import shuffle 　 from sklearn import preprocessing flags = tf.app.flags FLAGS = flags.FLAGS df = pd.read_csv( "./wine.csv", header=0) print (df.describe()) #df['displacement']=df['displacement'].astype(float) X = df[df.columns[1:13]].values y = df['Wine'].values-1 Y = tf.one_hot(indices = y, depth=3, on_value = 1., off_value = 0., axis = 1 , name = "a").eval() X, Y = shuffle (X, Y) scaler = preprocessing.StandardScaler() X = scaler.fit_transform(X) # Create the model x = tf.placeholder(tf.float32, [None, 12]) W = tf.Variable(tf.zeros([12, 3])) b = tf.Variable(tf.zeros([3])) y = tf.nn.softmax(tf.matmul(x, W) + b) # Define loss and optimizer y_ = tf.placeholder(tf.float32, [None, 3]) cross_entropy = tf.reduce_mean(-tf.reduce_sum(y_ * tf.log(y), reduction_indices=[1])) train_step = tf.train.GradientDescentOptimizer(0.1).minimize(cross_entropy) # Train tf.initialize_all_variables().run() for i in range(100): X,Y =shuffle (X, Y, random_state=1) Xtr=X[0:140,:] Ytr=Y[0:140,:] Xt=X[140:178,:] Yt=Y[140:178,:] Xtr, Ytr = shuffle (Xtr, Ytr, random_state=0) #batch_xs, batch_ys = mnist.train.next_batch(100) batch_xs, batch_ys = Xtr , Ytr train_step.run({x: batch_xs, y_: batch_ys}) cost = sess.run (cross_entropy, feed_dict={x: batch_xs, y_: batch_ys}) # Test trained model correct_prediction = tf.equal(tf.argmax(y, 1), tf.argmax(y_, 1)) accuracy = tf.reduce_mean(tf.cast(correct_prediction, tf.float32)) print(accuracy.eval({x: Xt, y_: Yt}))5.5　小结

在本章中，我们开始学习TensorFlow最强的功能：神经网络模型。

通过使用生成模型和实验模型，我们同时实现了神经网络的回归和分类。

在下一章中，我们将会深入新的模型结构，并且将神经网络模型用到其他的知识领域，如将卷积神经网络用于计算机视觉。

本文摘自《TensorFlow机器学习项目实战》

T ensorFlow机器学习项目实战

• 作者： 【阿根廷】Rodolfo Bonnin

TensorFlow是Google所主导的机器学习框架，也是机器学习领域研究和应用的热门对象。 本书主要介绍如何使用TensorFlow库实现各种各样的模型，旨在降低学习门槛，并为读者解决问题提供详细的方法和指导。全书共10章，分别介绍了TensorFlow基础知识、聚类、线性回归、逻辑回归、不同的神经网络、规模化运行模型以及库的应用技巧。 本书适合想要学习和了解 TensorFlow 和机器学习的读者阅读参考。如果读者具备一定的C++和Python的经验，将能够更加轻松地阅读和学习本书。

试读：

原文中此处为链接，暂不支持采集

购书：

原文中此处为链接，暂不支持采集

本书目录：(滑动手机查看)

第1章　探索和转换数据 1

1．1　TensorFlow的主要数据结构—张量 1

1．1．1　张量的属性—阶、形状和类型 1

1．1．2　创建新的张量 3

1．1．3　动手工作—与TensorFlow交互 4

1．2　处理计算工作流—TensorFlow的数据流图 5

1．2．1　建立计算图 5

1．2．2　数据供给 6

1．2．3　变量 6

1．2．4　保存数据流图 6

1．3　运行我们的程序—会话 8

1．4　基本张量方法 8

1．4．1　简单矩阵运算 8

1．4．2　序列 11

1．4．3　张量形状变换 12

1．4．4　数据流结构和结果可视化—TensorBoard 14

1．5　从磁盘读取信息 18

1．5．1　列表格式—CSV 18

1．5．2　读取图像数据 19

1．5．3　加载和处理图像 20

1．5．4　读取标准TensorFlow格式 21

1．6　小结 21

第2章　聚类 22

2．1　从数据中学习—无监督学习 22

2．2　聚类的概念 22

2．3　k均值 23

2．3．1　k均值的机制 23

2．3．2　算法迭代判据 23

2．3．3　k均值算法拆解 24

2．3．4　k均值的优缺点 25

2．4　k最近邻 25

2．4．1　k最近邻算法的机制 26

2．4．2　k-nn的优点和缺点 26

2．5　有用的库和使用示例 27

2．5．1　matplotlib绘图库 27

2．5．2　scikit-learn数据集模块 28

2．5．3　人工数据集类型 28

2．6　例1—对人工数据集的k均值

聚类 29

2．6．1　数据集描述和加载 29

2．6．2　模型架构 30

2．6．3　损失函数描述和优化循环 31

2．6．4　停止条件 31

2．6．5　结果描述 31

2．6．6　每次迭代中的质心变化 32

2．6．7　完整源代码 32

2．6．8　k均值用于环状数据集 34

2．7　例2—对人工数据集使用最近邻算法 36

2．7．1　数据集生成 36

2．7．2　模型结构 36

2．7．3　损失函数描述 37

2．7．4　停止条件 37

2．7．5　结果描述 37

2．7．6　完整源代码 37

2．8　小结 39

第3章　线性回归 40

3．1　单变量线性模型方程 40

3．2　选择损失函数 41

3．3　最小化损失函数 42

3．3．1　最小方差的全局最小值 42

3．3．2　迭代方法：梯度下降 42

3．4　示例部分 43

3．4．1　TensorFlow中的优化方法—训练模块 43

3．4．2　tf．train．Optimizer类 43

3．4．3　其他Optimizer实例类型 44

3．5　例1—单变量线性回归 44

3．5．1　数据集描述 45

3．5．2　模型结构 45

3．5．3　损失函数描述和Optimizer 46

3．5．4　停止条件 48

3．5．5　结果描述 48

3．5．6　完整源代码 49

3．6　例2—多变量线性回归 51

3．6．1　有用的库和方法 51

3．6．2　Pandas库 51

3．6．3　数据集描述 51

3．6．4　模型结构 53

3．6．5　损失函数和Optimizer 54

3．6．6　停止条件 55

3．6．7　结果描述 55

3．6．8　完整源代码 56

3．7　小结 57

第4章　逻辑回归 58

4．1　问题描述 58

4．2　Logistic函数的逆函数—Logit函数 59

4．2．1　伯努利分布 59

4．2．2　联系函数 60

4．2．3　Logit函数 60

4．2．4　对数几率函数的逆函数—Logistic函数 60

4．2．5　多类分类应用—Softmax回归 62

4．3　例1—单变量逻辑回归 64

4．3．1　有用的库和方法 64

4．3．2　数据集描述和加载 65

4．3．3　模型结构 67

4．3．4　损失函数描述和优化器循环 67

4．3．5　停止条件 68

4．3．6　结果描述 68

4．3．7　完整源代码 69

4．3．8　图像化表示 71

4．4　例2—基于skflow单变量逻辑回归 72

4．4．1　有用的库和方法 72

4．4．2　数据集描述 72

4．4．3　模型结构 72

4．4．4　结果描述 73

4．4．5　完整源代码 74

4．5　小结 74

第5章　简单的前向神经网络 75

5．1　基本概念 75

5．1．1　人工神经元 75

5．1．2　神经网络层 76

5．1．3　有用的库和方法 78

5．2　例1—非线性模拟数据回归 79

5．2．1　数据集描述和加载 79

5．2．2　数据集预处理 80

5．2．3　模型结构—损失函数描述 80

5．2．4　损失函数优化器 80

5．2．5　准确度和收敛测试 80

5．2．6　完整源代码 80

5．2．7　结果描述 81

5．3　例2—通过非线性回归，对汽车燃料效率建模 82

5．3．1　数据集描述和加载 82

5．3．2　数据预处理 83

5．3．3　模型架构 83

5．3．4　准确度测试 84

5．3．5　结果描述 84

5．3．6　完整源代码 84

5．4　例3—多类分类：葡萄酒分类 86

5．4．1　数据集描述和加载 86

5．4．2　数据集预处理 86

5．4．3　模型架构 87

5．4．4　损失函数描述 87

5．4．5　损失函数优化器 87

5．4．6　收敛性测试 88

5．4．7　结果描述 88

5．4．8　完整源代码 88

5．5　小结 89

第6章　卷积神经网络 90

6．1　卷积神经网络的起源 90

6．1．1　卷积初探 90

6．1．2　降采样操作—池化 95

6．1．3　提高效率—dropout操作 98

6．1．4　卷积类型层构建办法 99

6．2　例1—MNIST数字分类 100

6．2．1　数据集描述和加载 100

6．2．2　数据预处理 102

6．2．3　模型结构 102

6．2．4　损失函数描述 103

6．2．5　损失函数优化器 103

6．2．6　准确性测试 103

6．2．7　结果描述 103

6．2．8　完整源代码 104

6．3　例2—CIFAR10数据集的图像分类 106

6．3．1　数据集描述和加载 107

6．3．2　数据集预处理 107

6．3．3　模型结构 108

6．3．4　损失函数描述和优化器 108

6．3．5　训练和准确性测试 108

6．3．6　结果描述 108

6．3．7　完整源代码 109

6．4　小结 110

第7章　循环神经网络和LSTM 111

7．1　循环神经网络 111

7．1．1　梯度爆炸和梯度消失 112

7．1．2　LSTM神经网络 112

7．1．3　其他RNN结构 116

7．1．4　TensorFlow LSTM有用的类和方法 116

7．2　例1—能量消耗、单变量时间序列数据预测 117

7．2．1　数据集描述和加载 117

7．2．2　数据预处理 118

7．2．3　模型结构 119

7．2．4　损失函数描述 121

7．2．5　收敛检测 121

7．2．6　结果描述 122

7．2．7　完整源代码 122

7．3　例2—创作巴赫风格的曲目 125

7．3．1　字符级模型 125

7．3．2　字符串序列和概率表示 126

7．3．3　使用字符对音乐编码—ABC音乐格式 126

7．3．4　有用的库和方法 128

7．3．5　数据集描述和加载 129

7．3．6　网络训练 129

7．3．7　数据集预处理 130

7．3．8　损失函数描述 131

7．3．9　停止条件 131

7．3．10　结果描述 131

7．3．11　完整源代码 132

7．4　小结 137

第8章　深度神经网络 138

8．1　深度神经网络的定义 138

8．2　深度网络结构的历史变迁 138

8．2．1　LeNet 5 138

8．2．2　Alexnet 139

8．2．3　VGG模型 139

8．2．4　第一代Inception模型 140

8．2．5　第二代Inception模型 141

8．2．6　第三代Inception模型 141

8．2．7　残差网络（ResNet） 142

8．2．8　其他的深度神经网络

结构 143

8．3　例子—VGG艺术风格转移 143

8．3．1　有用的库和方法 143

8．3．2　数据集描述和加载 143

8．3．3　数据集预处理 144

8．3．4　模型结构 144

8．3．5　损失函数 144

8．3．6　收敛性测试 145

8．3．7　程序执行 145

8．3．8　完整源代码 146

8．4　小结 153

第9章　规模化运行模型—GPU和

服务 154

9．1　TensorFlow中的GPU支持 154

9．2　打印可用资源和设备参数 155

9．2．1　计算能力查询 155

9．2．2　选择CPU用于计算 156

9．2．3　设备名称 156

9．3　例1—将一个操作指派给

GPU 156

9．4　例2—并行计算Pi的数值 157

9．4．1　实现方法 158

9．4．2　源代码 158

9．5　分布式TensorFlow 159

9．5．1　分布式计算组件 159

9．5．2　创建TensorFlow集群 160

9．5．3　集群操作—发送计算方法

到任务 161

9．5．4　分布式编码结构示例 162

9．6　例3—分布式Pi计算 163

9．6．1　服务器端脚本 163

9．6．2　客户端脚本 164

9．7　例4—在集群上运行分布式

模型 165

9．8　小结 168

第10章　库的安装和其他技巧 169

10．1　Linux安装 169

10．1．1　安装要求 170

10．1．2　Ubuntu安装准备（安装操作的

前期操作） 170

10．1．3　Linux下通过pip安装

TensorFlow 170

10．1．4　Linux下从源码安装

TensorFlow 175

10．2　Windows安装 179

10．2．1　经典的Docker工具箱

方法 180

10．2．2　安装步骤 180

10．3　MacOS X安装 183

10．4　小结 185

小福利

关注【异步社区】服务号，转发本文至朋友圈或 50 人以上微信群，截图发送至异步社区服务号后台，并在文章底下留言，分享你的机器学习、深度学习开发经验或者本书的试读体验，我们将从符合活动规则的读者中，随机选出 2位用户送出《TensorFlow机器学习项目实战》一本，赶快积极参与吧！

活动截止时间：2017 年 12月24日

上期获奖名单

风何悦 anjiadoo

请获奖读者填写下方获奖信息，活动名称《异步社区Go Web编程》

原文中此处为链接，暂不支持采集

原文中此处为链接，暂不支持采集

点击图片参与活动

在“异步社区”后台回复“关注”，即可免费获得2000门在线视频课程；推荐朋友关注根据提示获取赠书链接，免费得异步图书一本。赶紧来参加哦！