[ Pytorch ] —— 代码使用经验总结
—— 教程网站合集 ——
丨官方文档丨官方教程丨
中文教程:丨网站01丨网站02丨
书籍资料:丨深度学习框架PyTorch:入门与实践丨
知乎经验
——————————
目录
一、基础知识理解汇总
一、自动求导机制(Autograd)
1、基本求导代码理解:
2、自动求导过程中的梯度
3、backwards中的retain_graph参数的作用:
4、自己定义可以自动求导的函数——扩展autograd
二、深度学习
一、loss
2-1 L1范数损失 L1Loss
2-2 均方误差损失 MSELoss
2-3 交叉熵损失 CrossEntropyLoss
2-4 KL 散度损失 KLDivLoss
2-5 二进制交叉熵损失 BCELoss
2-6 BCEWithLogitsLoss
2-7 MarginRankingLoss
2-8 HingeEmbeddingLoss
2-9 多标签分类损失 MultiLabelMarginLoss
2-10 平滑版L1损失 SmoothL1Loss
2-11 2分类的logistic损失 SoftMarginLoss
2-12 多标签 one-versus-all 损失 MultiLabelSoftMarginLoss
2-13 cosine 损失 CosineEmbeddingLoss
2-14 多类别分类的hinge损失 MultiMarginLoss
2-15 三元组损失 TripletMarginLoss
2-16 连接时序分类损失 CTCLoss
2-17 负对数似然损失 NLLLoss
2-18 NLLLoss2d
2-19 PoissonNLLLoss
三、 编程中的使用经验汇总
一、数据处理
1 、torch的tensor 、variable与 numpy的array 相互转换。
2、把标签(一个标量数据)变成使用One-hot编码的方法:
3、torch.Tensor中的各种数据类型转换方法:
4、对numpy矩阵 和 torch.Tensor的形状理解:
5、torch.Tensor的相乘法则:
6、列表(list)转换成torch.Tensor的方法。
7、常用的 改变形状 的方法合集。
# 一些资源汇总
二、模型使用
1、model.named_children读取模型的名称与模型。
一、基础知识理解汇总
一、自动求导机制(Autograd)
扩展:丨博客01丨
1、基本求导代码理解:
# ———— output: scalar(输出是标量时候)
x = torch.ones(1, requires_grad=True) # x = 1
y = 2 * x ** 2 # y=2*x^2 ,其中 x = 1, y是1维
gradients = torch.tensor([0.1], dtype=torch.float) # [0.1] 表示各个维度上导函数前的权重
y.backward(gradients) # y'= ∂(2*x^2)/∂x = 4x
print(x.grad) # x在x=1时候的 导数值
[输出结果]>> tensor([ 0.4000])# ———— output: tensor(输出是多个值)
x = torch.ones(3, requires_grad=True) # x = [1,1,1]
y = 2 * x ** 2 # y=2*x^2 ,其中 x = [1,1,1], y是3维
gradients = torch.tensor([0.1, 1.0, 0.0001], dtype=torch.float) # [0.1, 1.0, 0.0001] 表示各个维度上导函数前的权重
y.backward(gradients) # y'= ∂(2*x^2)/∂x = 4x
print(x.grad) # x在x=[1,1,1]时候的 导数值
[输出结果] >> tensor([ 0.4000, 4.0000, 0.0004])
2、自动求导过程中的梯度
自动求导过程中,只会保留叶子节点的梯度:参考:丨链接1丨链接2丨
import torch
x = torch.Tensor([0, 1, 2, 3]).requires_grad_()
y = torch.Tensor([4, 5, 6, 7]).requires_grad_()
w = torch.Tensor([1, 2, 3, 4]).requires_grad_()
z = x+y
# ===================
def hook_fn(grad):
print(grad)
z.register_hook(hook_fn)
# ===================
o = w.matmul(z)
print('=====Start backprop=====')
o.backward()
print('=====End backprop=====')
print('x.grad:', x.grad)
print('y.grad:', y.grad)
print('w.grad:', w.grad)
print('z.grad:', z.grad)
【运行结果】
=====Start backprop=====
tensor([1., 2., 3., 4.])
=====End backprop=====
x.grad: tensor([1., 2., 3., 4.])
y.grad: tensor([1., 2., 3., 4.])
w.grad: tensor([ 4., 6., 8., 10.])
z.grad: None
3、backwards中的retain_graph参数的作用:
转载自:丨博客丨
其实retain_graph这个参数在平常中我们是用不到的,但是在特殊的情况下我们会用到它:
假设一个我们有一个输入x,y = x **2, z = y*4,然后我们有两个输出,一个output_1 = z.mean(),另一个output_2 = z.sum()。然后我们对两个output执行backward。
In[3]: import torch
In[5]: x = torch.randn((1,4),dtype=torch.float32,requires_grad=True)
In[6]: y = x ** 2
In[7]: z = y * 4
In[8]: output1 = z.mean()
In[9]: output2 = z.sum()
In[10]: output1.backward() # 这个代码执行正常,但是执行完中间变量都free了,所以下一个出现了问题
In[11]: output2.backward() # 这时会引发错误
Traceback (most recent call last):
File "/home/prototype/anaconda3/envs/pytorch-env/lib/python3.6/site-packages/IPython/core/interactiveshell.py", line 2963, in run_code
exec(code_obj, self.user_global_ns, self.user_ns)
File "", line 1, in
output2.backward()
File "/home/prototype/anaconda3/envs/pytorch-env/lib/python3.6/site-packages/torch/tensor.py", line 93, in backward
torch.autograd.backward(self, gradient, retain_graph, create_graph)
File "/home/prototype/anaconda3/envs/pytorch-env/lib/python3.6/site-packages/torch/autograd/__init__.py", line 89, in backward
allow_unreachable=True) # allow_unreachable flag
RuntimeError: Trying to backward through the graph a second time, but the buffers have already been freed. Specify retain_graph=True when calling backward the first time. 如果我们这样写:
In[3]: import torch
...: from torch.autograd import Variable
...: x = torch.randn((1,4),dtype=torch.float32,requires_grad=True)
...: y = x ** 2
...: z = y * 4
...: output1 = z.mean()
...: output2 = z.sum()
...: output1.backward(retain_graph=True) # 这里参数表明保留backward后的中间参数。
...: output2.backward()有两个输出的时候就需要用到这个参数,这就和之前提到的风格迁移中Content Loss层为什么使用这个参数有了联系,因为在风格迁移中不只有Content Loss层还有Style Loss层,两个层都公用一个神经网络的参数但是有两个loss的输出,因此需要retain_graph参数为True去保留中间参数从而两个loss的backward()不会相互影响。
也就相当于,假如你有两个Loss:
# 假如你有两个Loss,先执行第一个的backward,再执行第二个backward
loss1.backward(retain_graph=True)
loss2.backward() # 执行完这个后,所有中间变量都会被释放,以便下一次的循环
optimizer.step() # 更新参数这样就比较容易理解了。
4、自己定义可以自动求导的函数——扩展autograd
以下转载自:链接
目前绝大多数函数都可以使用autograd实现反向求导,但如果需要自己写一个复杂的函数,不支持自动反向求导怎么办? 写一个Function,实现它的前向传播和反向传播代码,Function对应于计算图中的矩形, 它接收参数,计算并返回结果。下面给出一个例子。
from torch.autograd import Function
class MultiplyAdd(Function):
@staticmethod
def forward(ctx, w, x, b):
print('type in forward', type(x))
ctx.save_for_backward(w, x)#存储用来反向传播的参数
output = w*x +b
return output
@staticmethod
def backward(ctx, grad_output):
w, x = ctx.saved_variables #deprecated,现在使用saved_tensors
print('type in backward',type(x))
grad_w = grad_output * x
grad_x = grad_output * w
grad_b = grad_output * 1
return grad_w, grad_x, grad_b分析如下:
- 自定义的Function需要继承autograd.Function,没有构造函数__init__,forward和backward函数都是静态方法
- forward函数的输入和输出都是Tensor,backward函数的输入和输出都是Variable
- backward函数的输出和forward函数的输入一一对应,backward函数的输入和forward函数的输出一一对应
- backward函数的grad_output参数即t.autograd.backward中的grad_variables
- 如果某一个输入不需要求导,直接返回None,如forward中的输入参数x_requires_grad显然无法对它求导,直接返回None即可
- 反向传播可能需要利用前向传播的某些中间结果,需要进行保存,否则前向传播结束后这些对象即被释放
Function的使用利用Function.apply(variable)
from torch.autograd import Function
class MultiplyAdd(Function):
@staticmethod
def forward(ctx, w, x, b):
print('type in forward', type(x))
ctx.save_for_backward(w, x)#存储用来反向传播的参数
output = w*x +b
return output
@staticmethod
def backward(ctx, grad_output):
w, x = ctx.saved_variables #deprecated,现在使用saved_tensors
print('type in backward',type(x))
grad_w = grad_output * x
grad_x = grad_output * w
grad_b = grad_output * 1
return grad_w, grad_x, grad_b调用方法
类名.apply(参数)
输出变量.backward()
from torch.autograd import Variable as V
x = V(t.ones(1))
w = V(t.rand(1),requires_grad=True)
b = V(t.rand(1),requires_grad=True)
print('开始前向传播')
z = MultiplyAdd.apply(w, x, b)
print('开始反向传播')
z.backward()
# x不需要求导,中间过程还是会计算它的导数,但随后被清空
x.grad, w.grad, b.grad
【结果】
开始前向传播
type in forward
开始反向传播
type in backward
(None, tensor([1.]), tensor([1.]))
二、深度学习
一、loss
损失函数通过torch.nn包实现,
基本用法
criterion = LossCriterion() #构造函数有自己的参数
loss = criterion(x, y) #调用标准时也有参数以下代码基本参考自丨博客丨
2-1 L1范数损失 L1Loss
计算 output 和 target 之差的绝对值。
torch.nn.L1Loss(reduction='mean')参数:
reduction-三个值:none: 不使用约简;mean:返回loss和的平均值; sum:返回loss的和。默认:mean。
2-2 均方误差损失 MSELoss
计算 output 和 target 之差的均方差。
torch.nn.MSELoss(reduction='mean')参数:
reduction-三个值,none: 不使用约简;mean:返回loss和的平均值; sum:返回loss的和。默认:mean。
2-3 交叉熵损失 CrossEntropyLoss
当训练有 C 个类别的分类问题时很有效. 可选参数 weight 必须是一个1维 Tensor, 权重将被分配给各个类别. 对于不平衡的训练集非常有效。在多分类任务中,经常采用 softmax 激活函数+交叉熵损失函数,因为交叉熵描述了两个概率分布的差异,然而神经网络输出的是向量,并不是概率分布的形式。所以需要 softmax激活函数将一个向量进行“归一化”成概率分布的形式,再采用交叉熵损失函数计算 loss。
torch.nn.CrossEntropyLoss(weight=None, ignore_index=-100, reduction='mean')参数:
weight (Tensor, optional) – 自定义的每个类别的权重. 必须是一个长度为 C 的 Tensor
ignore_index (int, optional) – 设置一个目标值, 该目标值会被忽略, 从而不会影响到 输入的梯度。
reduction-三个值,none: 不使用约简;mean:返回loss和的平均值; sum:返回loss的和。默认:mean。
2-4 KL 散度损失 KLDivLoss
计算 input 和 target 之间的 KL 散度。KL 散度可用于衡量不同的连续分布之间的距离, 在连续的输出分布的空间上(离散采样)上进行直接回归时 很有效.
torch.nn.KLDivLoss(reduction='mean')参数:
reduction-三个值,none: 不使用约简;mean:返回loss和的平均值; sum:返回loss的和。默认:mean。
2-5 二进制交叉熵损失 BCELoss
二分类任务时的交叉熵计算函数。用于测量重构的误差, 例如自动编码机. 注意目标的值 t[i] 的范围为0到1之间.
torch.nn.BCELoss(weight=None, reduction='mean')参数:
weight (Tensor, optional) – 自定义的每个 batch 元素的 loss 的权重. 必须是一个长度为 “nbatch” 的 的 Tensor
2-6 BCEWithLogitsLoss
BCEWithLogitsLoss损失函数把 Sigmoid 层集成到了 BCELoss 类中. 该版比用一个简单的 Sigmoid 层和 BCELoss 在数值上更稳定, 因为把这两个操作合并为一个层之后, 可以利用 log-sum-exp 的 技巧来实现数值稳定.
torch.nn.BCEWithLogitsLoss(weight=None, reduction='mean', pos_weight=None)参数:
weight (Tensor, optional) – 自定义的每个 batch 元素的 loss 的权重. 必须是一个长度 为 “nbatch” 的 Tensor
2-7 MarginRankingLoss
torch.nn.MarginRankingLoss(margin=0.0, reduction='mean')对于 mini-batch(小批量) 中每个实例的损失函数如下:
参数:
margin:默认值0
2-8 HingeEmbeddingLoss
torch.nn.HingeEmbeddingLoss(margin=1.0, reduction='mean')对于 mini-batch(小批量) 中每个实例的损失函数如下:
参数:
margin:默认值1
2-9 多标签分类损失 MultiLabelMarginLoss
torch.nn.MultiLabelMarginLoss(reduction='mean')对于mini-batch(小批量) 中的每个样本按如下公式计算损失:
2-10 平滑版L1损失 SmoothL1Loss
也被称为 Huber 损失函数。
torch.nn.SmoothL1Loss(reduction='mean')其中
2-11 2分类的logistic损失 SoftMarginLoss
torch.nn.SoftMarginLoss(reduction='mean')
2-12 多标签 one-versus-all 损失 MultiLabelSoftMarginLoss
torch.nn.MultiLabelSoftMarginLoss(weight=None, reduction='mean')
2-13 cosine 损失 CosineEmbeddingLoss
torch.nn.CosineEmbeddingLoss(margin=0.0, reduction='mean')
1
参数:
margin:默认值0
2-14 多类别分类的hinge损失 MultiMarginLoss
torch.nn.MultiMarginLoss(p=1, margin=1.0, weight=None, reduction='mean')
1
参数:
p=1或者2 默认值:1
margin:默认值1
2-15 三元组损失 TripletMarginLoss
torch.nn.TripletMarginLoss(margin=1.0, p=2.0, eps=1e-06, swap=False, reduction='mean')
1
其中:
2-16 连接时序分类损失 CTCLoss
CTC连接时序分类损失,可以对没有对齐的数据进行自动对齐,主要用在没有事先对齐的序列化数据训练上。比如语音识别、ocr识别等等。
torch.nn.CTCLoss(blank=0, reduction='mean')
1
参数:
reduction-三个值,none: 不使用约简;mean:返回loss和的平均值; sum:返回loss的和。默认:mean。
2-17 负对数似然损失 NLLLoss
负对数似然损失. 用于训练 C 个类别的分类问题.
torch.nn.NLLLoss(weight=None, ignore_index=-100, reduction='mean')
1
参数:
weight (Tensor, optional) – 自定义的每个类别的权重. 必须是一个长度为 C 的 Tensor
ignore_index (int, optional) – 设置一个目标值, 该目标值会被忽略, 从而不会影响到 输入的梯度.
2-18 NLLLoss2d
对于图片输入的负对数似然损失. 它计算每个像素的负对数似然损失.
torch.nn.NLLLoss2d(weight=None, ignore_index=-100, reduction='mean')
1
参数:
weight (Tensor, optional) – 自定义的每个类别的权重. 必须是一个长度为 C 的 Tensor
reduction-三个值,none: 不使用约简;mean:返回loss和的平均值; sum:返回loss的和。默认:mean。
2-19 PoissonNLLLoss
目标值为泊松分布的负对数似然损失
torch.nn.PoissonNLLLoss(log_input=True, full=False, eps=1e-08, reduction='mean')
1
参数:
log_input (bool, optional) – 如果设置为 True , loss 将会按照公 式 exp(input) - target * input 来计算, 如果设置为 False , loss 将会按照 input - target * log(input+eps) 计算.
full (bool, optional) – 是否计算全部的 loss, i. e. 加上 Stirling 近似项 target * log(target) - target + 0.5 * log(2 * pi * target).
eps (float, optional) – 默认值: 1e-8
参考资料
pytorch loss function 总结
---------------------
作者:mingo_敏
来源:CSDN
原文:https://blog.csdn.net/shanglianlm/article/details/85019768
版权声明:本文为博主原创文章,转载请附上博文链接!
三、 编程中的使用经验汇总
一、数据处理
1 、torch的tensor 、variable与 numpy的array 相互转换。
- tensor⇒array
x = torch.tensor([[1, 2, 3], [4, 5, 6]])
x = x.numpy()
print(x)
>>[[1 2 3]
[4 5 6]]- array⇒tensor
x = torch.tensor([[1, 2, 3], [4, 5, 6]])
x = x.numpy()
x = torch.from_numpy(x)
print(x)
>>tensor([[ 1, 2, 3],
[ 4, 5, 6]])- Variable=>np.array
# 将Variable张量转化为numpy
x = torch.autograd.Variable(torch.FloatTensor(8,100,1,1))
x = x.data.numpy()- np.array=>Variable
# 将numpy转化为Variable张量
x = np.array([8, 3, 64, 64])
x = torch.from_numpy(x)
x = torch.autograd.Variable(x)2、把标签(一个标量数据)变成使用One-hot编码的方法:
方法1:
参考:https://discuss.pytorch.org/t/convert-int-into-one-hot-format/507/4
import torch.utils.data
import torch
import torch.nn as nn
import torch.nn.functional as F
import torchvision
import torchvision.transforms as transforms
import numpy as np
import pickle
a,b = cifar_trans_with_labels[0]
# print('a=',a,'b=',b)
import torch
batch_size = 1
nb_digits = 10
print('b是个标量:',b) # b 是cifar-10中的标签,是个标量。
labels_onehot = torch.FloatTensor(batch_size, nb_digits)
labels=np.array([b]) # 把标量b变成一维numpy矩阵。
print('labels_numpy:',labels)
print('labels_numpy_size:',labels.shape) # labels_numpy_size: (1,), 一项就是一维。
labels = torch.from_numpy(labels) # 变成torch.Tensor
labels = labels.long() # 下面的 labels_onehot.scatter_(1, labels, 1) 需要labels中的数据是long类型。
labels = labels.view(1,-1)
print('labels_torchTensor_shape:',labels.shape)
print('labels_torchTensor_value:',labels)
labels_onehot.zero_()
labels_onehot.scatter_(1, labels, 1) # 变成one-hot编码。
print('labels_One-shot:',labels_onehot)
print('labels_One-shot_shape:',labels_onehot.shape)
print('labels_One-shot_tensortype:',labels_onehot.type())
【结果】
b是个标量: 6
labels_numpy: [6]
labels_numpy_size: (1,)
labels_torchTensor_shape: torch.Size([1, 1])
labels_torchTensor_value: tensor([[ 6]])
labels_One-shot: tensor([[ 0., 0., 0., 0., 0., 0., 1., 0., 0., 0.]])
labels_One-shot_shape: torch.Size([1, 10])
labels_One-shot_tensortype: torch.FloatTensor方法2:tensor.scatter_()函数
import torch
log_probs = torch.FloatTensor(torch.rand([4,10])) # shape: [batch_size, num_class]
targets = torch.FloatTensor([1,2,3,4]) # shape: [batch_size]
targets = targets.long()
unsquee_targets = targets.unsqueeze(1).data.cpu() # index which is used to fill '1' into right location in one-hot tensor of target
print(unsquee_targets)
targets = torch.zeros(log_probs.size()).scatter_(1, unsquee_targets, 1)
print(targets)
【结果】
tensor([[1],
[2],
[3],
[4]])
tensor([[0., 1., 0., 0., 0., 0., 0., 0., 0., 0.],
[0., 0., 1., 0., 0., 0., 0., 0., 0., 0.],
[0., 0., 0., 1., 0., 0., 0., 0., 0., 0.],
[0., 0., 0., 0., 1., 0., 0., 0., 0., 0.]])
3、torch.Tensor中的各种数据类型转换方法:
https://ptorch.com/news/71.html
4、对numpy矩阵 和 torch.Tensor的形状理解:
(1)、形状理解:
import numpy as np
import torch
a = [
[
3,4,6
]
]
#注:a 是个列表。
a_nparray = np.array(a)
print('a变成np矩阵后a_nparray:',a_nparray)
print('a变成np矩阵后a_nparray的形状:',a_nparray.shape)
print('形状为 (1, 3) 的意义就是:①有几个项就表示几个维度,这里有 1,3 两个项,因此a_nparray是二维矩阵;'
'②每一项的值表示这一维有几个元素。')
print('')
a_torchtensor = torch.from_numpy(a_nparray)
print('a转化为torch.Tensor之后:',a_torchtensor)
print('a转化为torch.Tensor之后的形状:',a_torchtensor.shape)
print('torch.Size([1, 3]) 就表示:①有几个项就表示几个维度,这里有 1,3 两个项,因此a_nparray是二维矩阵;'
'②每一项的值表示这一维有几个元素。')(2)、0维矩阵 与 0维tensor (即:标量):
import torch
import numpy as np
a = 1
print('标量a的值:', a)
a_nparray = np.array(a)
print('a变成np矩阵后的形状:',a_nparray.shape)
print('() 就表示是标量,即0维')
a_torchtensor = torch.from_numpy(a_nparray)
print('a转化为torch.Tensor之后:',a_torchtensor)
print('a转化为torch.Tensor之后的形状:',a_torchtensor.shape)
print('torch.Size([]) 就表示是标量,即0维tensor')
(3)、如何数numpy或者torch.Tensor的维度
import torch
x = torch.tensor([[1], [2], [3]])
print(x.shape)
【结果】
torch.Size([3, 1])(4) axis与shape的关系
5、torch.Tensor的相乘法则:
(1)、普通相乘: c = A * B
规则:A和B对应维度的对应位置相乘。
import torch
input = torch.Tensor([[1,2],
[1,2]]) # size:[2,2]
print('input_shape: ', input.shape)
yaw = torch.Tensor( [ [10], [20] ] ) # size:[2, 1]
print('yaw_shape: ', yaw.shape)
yaw = yaw.view(yaw.size(0),1) # yaw 的shape为:[256, 1]
print('after yaw_view:', yaw)
print('after yaw_view shape:', yaw.shape)
yaw = yaw.expand_as(input)
print('after yaw_view_expand:', yaw)
print('after yaw_view_expand shape:', yaw.shape)
# output= yaw * input
output= input * yaw # tensor 对应维度的 对应位置元素 相乘。
print('output:', output)
print('output.shape', output.shape)
6、列表(list)转换成torch.Tensor的方法。
import torch
import os
os.environ["CUDA_VISIBLE_DEVICES"] = "2"
aa = torch.rand(3,256,128)
bb = []
bb.append(aa)
bb.append(aa)
print(torch.stack(bb).shape)
【结果】
>>> torch.size([2,3,256,128])
7、常用的 改变形状 的方法合集。
(1) [tensor].unsqueeze(dim)
作用:在[tensor]的指定位置dim添加一个维度。
import torch
import torchvision
from torch.autograd import Variable
targets = torch.rand(128)
print(targets.shape)
targets_uns = targets.unsqueeze(1).data.cpu() # 在targets的第2个维度上增加一个维度
print(targets_uns.shape)
【结果】
>>> torch.Size([128])
>>> torch.Size([128, 1])
(2) [Tensor].scatter_(dim, index, src)
作用:在 [Tensor] 中 的指定位置填入相应的值。将src中数据根据index中的索引按照dim的方向填进[Tensor]中。
import torch
import torchvision
from torch.autograd import Variable
pred = torch.rand(128,702)
pred = Variable(pred)
logsoftmax= torch.nn.LogSoftmax(dim=1)
log_probs = logsoftmax(pred)
targets = torch.rand(128)
targets =targets.long()
targets = Variable(targets)
print(pred.shape)
print(log_probs.shape)
print(targets.shape)
zeros = torch.zeros(log_probs.size())
targets_uns = targets.unsqueeze(1).data.cpu()
print(targets_uns.shape)
targets = zeros.scatter_(1, targets_uns, 1)
print(targets.shape)
【结果】
>>> torch.Size([128, 702])
>>> torch.Size([128, 702])
>>> torch.Size([128])
>>> torch.Size([128, 1])
>>> torch.Size([128, 702])
(3) 重复张量
orch.Tensor.repeat(*sizes)
沿着指定的维度重复张量。不同于expand()方法,本函数复制的是张量中的数据。
参数:
- size (torch.size or int…) - 沿着每一维重复的次数
x = torch.Tensor([1, 2, 3])
x.repeat(4, 2)
1 2 3 1 2 3
1 2 3 1 2 3
1 2 3 1 2 3
1 2 3 1 2 3
[torch.FloatTensor of size 4x6]
# 一些资源汇总
1、pytorch张量维度操作(拼接、维度扩展、压缩、转置、重复……)。
二、模型使用
1、model.named_children读取模型的名称与模型。
import torch.nn as nn
import torch.nn.functional as F
class Net(nn.Module):
def __init__(self):
super(Net, self).__init__()
self.conv1 = nn.Conv2d(3, 6, 5)
self.pool = nn.MaxPool2d(2, 2)
self.conv2 = nn.Conv2d(6, 16, 5)
self.fc1 = nn.Linear(16 * 5 * 5, 120)
self.fc2 = nn.Linear(120, 84)
self.fc3 = nn.Linear(84, 10)
def forward(self, x):
x = self.pool(F.relu(self.conv1(x)))
x = self.pool(F.relu(self.conv2(x)))
x = x.view(-1, 16 * 5 * 5)
x = F.relu(self.fc1(x))
x = F.relu(self.fc2(x))
x = self.fc3(x)
return x
net = Net()
for name, module in net.named_children():
print('name:\t', name)
print('module:\t', module)
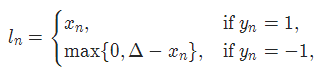
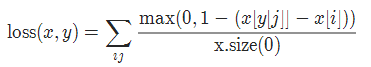
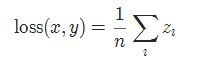
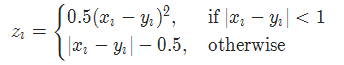
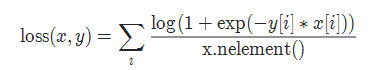
![[ Pytorch ] —— 代码使用经验总结_第1张图片](http://img.e-com-net.com/image/info8/6e0de22245da4fba94c5fa6e6020d266.png)
![[ Pytorch ] —— 代码使用经验总结_第2张图片](http://img.e-com-net.com/image/info8/b0314384f1c84d6d87375ff3fb2e3ca5.png)
![[ Pytorch ] —— 代码使用经验总结_第3张图片](http://img.e-com-net.com/image/info8/8d8ac413388042649c922eecb0253a32.png)