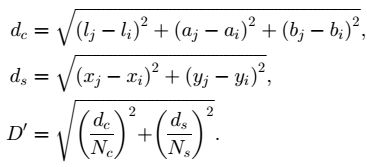SLIC超像素分割
超体素概念:
超体素概念是2003年Xiaofeng Ren提出和发展起来的图像分割技术,是指具有相似纹理、颜色、亮度等特征的相邻像素构成的有一定视觉意义的不规则像素块。它利用像素之间特征的相似性将像素分组,用少量的超像素代替大量的像素来表达图片特征,很大程度上降低了图像后处理的复杂度,所以通常作为分割算法的预处理步骤。已经广泛用于图像分割、目标识别等计算机视觉领域。
简单的线性迭代聚类:
简单的线性迭代聚类(simple linear iterative clustering,SLIC)。它是2010年Achanta,Radhakrishna等提出的一种思想简单、实现方便的算法,将彩色图像转化为LAB颜色空间和XY坐标下的5维特征向量,然后对5维特征向量构造距离度量标准,对图像像素进行局部聚类的过程。SLIC算法能生成紧凑、近似均匀的超像素,在运算速度,物体轮廓保持、超像素形状方面具有较高的综合评价,比较符合人们期望的分割效果。
SLIC主要优点总结如下:
1)生成的超像素如同细胞一般紧凑整齐,邻域特征比较容易表达。这样基于像素的方法可以比较容易的改造为基于 超像素的方法;
2)不仅可以分割彩色图,也可以兼容分割灰度图;
3)需要设置的参数非常少,默认情况下只需要设置一个预分割的超像素的数量;
4)相比其他的超像素分割方法,SLIC在运行速度、生成超像素的紧凑度、轮廓保持方面都比较理想。
Lab颜色空间简介:
Lab色彩模型是由亮度(L)和有关色彩的a, b三个要素组成。L表示亮度(Luminosity),L的值域由0(黑色)到100(白色)。a表示从洋红色至绿色的范围(a为负值指示绿色而正值指示品红),b表示从黄色至蓝色的范围(b为负值指示蓝色而正值指示黄色)。
Lab颜色空间的优点:
1)不像RGB和CMYK色彩空间,Lab 颜色被设计来接近人类生理视觉。它致力于感知均匀性,它的 L 分量密切匹配 人类亮度感知。因此可以被用来通过修改 a 和 b 分量的输出色阶来做精确的颜色平衡,或使用 L 分量来调整亮度对比。这些变换在 RGB 或 CMYK 中是困难或不可能的;
2)因为 Lab 描述的是颜色的显示方式,而不是设备(如显示器、打印机或数码相机)生成颜色所需的特定色料的数 量,所以 Lab 被视为与设备无关的颜色模型;
3)色域宽阔。它不仅包含了RGB,CMYK的所有色域,还能表现它们不能表现的色彩。人的肉眼能感知的色彩,都 能通过Lab模型表现出来。另外,Lab色彩模型的绝妙之处还在于它弥补了RGB色彩模型色彩分布不均的不足,因为RGB模型在蓝色到绿色之间的过渡色彩过多,而在绿色到红色之间又缺少黄色和其他色彩。如果我们想在数字图形的处理中保留尽量宽阔的色域和丰富的色彩,最好选择Lab。
下面描述一下SLIC具体实现的步骤:
1. 初始化种子点(聚类中心):按照设定的超像素个数,在图像内均匀的分配种子点。假设图片总共有 N 个像素点,预分割为 K 个相同尺寸的超像素,那么每个超像素的大小为N/ K ,则相邻种子点的距离(步长)近似为S=sqrt(N/K);
2. 在种子点的n*n邻域内重新选择种子点(一般取n=3)。具体方法为:计算该邻域内所有像素点的梯度值,将种子点移到该邻域内梯度最小的地方。这样做的目的是为了避免种子点落在梯度较大的轮廓边界上,以免影响后续聚类效果;
3. 在每个种子点周围的邻域内为每个像素点分配类标签(即属于哪个聚类中心)。和标准的k-means在整张图中搜索不同,SLIC的搜索范围限制为2S*2S,可以加速算法收敛,如下图。在此注意一点:期望的超像素尺寸为S*S,但是搜索的范围是2S*2S;
4. 距离度量。包括颜色距离和空间距离。对于每个搜索到的像素点,分别计算它和该种子点的距离。距离计算方法如下:
其中,dc代表颜色距离,ds代表空间距离,Ns是类内最大空间距离,定义为Ns=S=sqrt(N/K),适用于每个聚类。最大的颜色距离Nc既随图片不同而不同,也随聚类不同而不同,所以我们取一个固定常数m(取值范围[1,40],一般取10)代替。最终的距离度量D'如下:
由于每个像素点都会被多个种子点搜索到,所以每个像素点都会有一个与周围种子点的距离,取最小值对应的种子点作为该像素点的聚类中心;
5. 迭代优化。理论上上述步骤不断迭代直到误差收敛(可以理解为每个像素点聚类中心不再发生变化为止),实践发现10次迭代对绝大部分图片都可以得到较理想效果,所以一般迭代次数取10;
6. 增强连通性。经过上述迭代优化可能出现以下瑕疵:出现多连通情况、超像素尺寸过小,单个超像素被切割成多个不连续超像素等,这些情况可以通过增强连通性解决。主要思路是:新建一张标记表,表内元素均为-1,按照“Z”型走向(从左到右,从上到下顺序)将不连续的超像素、尺寸过小超像素重新分配给邻近的超像素,遍历过的像素点分配给相应的标签,直到所有点遍历完毕为止。
参考文献:
[1] Achanta,Radhakrishna, et al. Slic superpixels. No. EPFL REPORT 149300. 2010.
[2] Achanta,Radhakrishna, et al. "SLIC superpixels compared to state-of-the-artsuperpixel methods." Pattern Analysis and Machine Intelligence, IEEETransactions on 34.11 (2012): 2274-2282.
转自:http://blog.csdn.net/electech6/article/details/45509779