ROC和AUC介绍及计算

        AUC是一种用来度量分类模型好坏的一个标准。它跟ROC有着密切的关系，所以先介绍ROC，再来分析AUC以及它的计算。

• ROC曲线

      ROC曲线能够反映分类的能力，它的横坐标是falsepositive rate(FPR)，纵坐标是truepositive rate(TPR)。（晕定义的可以跳到下一段）对某个分类器而言，我们可以根据其在测试样本上的表现得到一个TPR和FPR点对。这样，此分类器就可以映射成ROC平面上的一个点。调整这个分类器分类时候使用的阈值，我们就可以得到一个经过(0,0)，(1, 1)的曲线，这就是此分类器的ROC曲线。一般情况下，这个曲线都应该处于(0,0)和(1, 1)连线的上方。因为(0, 0)和(1, 1)连线形成的ROC曲线实际上代表的是一个随机分类器。如果很不幸，你得到一个位于此直线下方的分类器的话，一个直观的补救办法就是把所有的预测结果反向，即：分类器输出结果为正类，则最终分类的结果为负类，反之，则为正类。总之，我们需要计算FPR和TPR，那这两个参数的具体计算方法是什么呢？

    针对一个二分类问题，将实例分成正类(postive)或者负类(negative)。但是实际中分类时，会出现四种情况.

(1)若一个实例是正类并且被预测为正类，即为真正类(True Postive TP)

(2)若一个实例是正类，但是被预测成为负类（漏报），即为假负类(False Negative FN)

(3)若一个实例是负类，但是被预测成为正类（误报），即为假正类(False Postive FP)

(4)若一个实例是负类，但是被预测成为负类，即为真负类(True Negative TN)

列联表如下，1代表正类，0代表负类：

		预测		合计
		1	0
实际	1 (P)	True Positive（TP）	False Negative（FN）	Actual Positive(TP+FN)
	0 (N)	False Positive（FP)	True Negative(TN)	Actual Negative(FP+TN)
合计		Predicted Positive(TP+FP)	Predicted Negative(FN+TN)	TP+FP+FN+TN

我们的ROC曲线如下图所示：

 

 

纵坐标是truepositive rate(TPR) = TP / (TP+FN=P)（分母是横行的合计）直观解释：实际是1中，猜对多少

横坐标是falsepositive rate(FPR) = FP / (FP+TN=N)直观解释：实际是0中，错猜多少

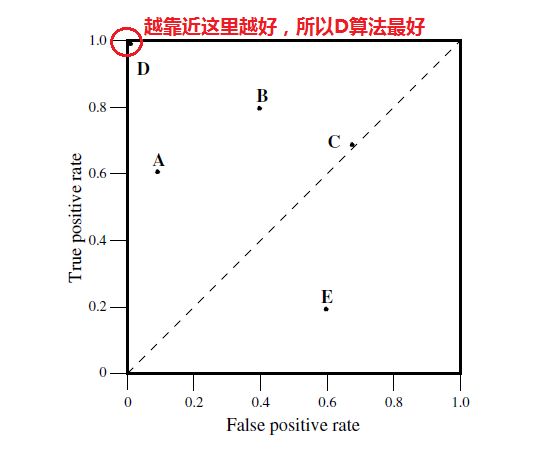
接下来我们考虑ROC曲线图中的四个点和一条线。第一个点，(0,1)，即FPR=0, TPR=1，这意味着FN（false negative）=0，并且FP（false positive）=0。Wow，这是一个完美的分类器，它将所有的样本都正确分类。第二个点，(1,0)，即FPR=1，TPR=0，类似地分析可以发现这是一个最糟糕的分类器，因为它成功避开了所有的正确答案。第三个点，(0,0)，即FPR=TPR=0，即FP（false positive）=TP（true positive）=0，可以发现该分类器预测所有的样本都为负样本（negative）。类似的，第四个点（1,1），分类器实际上预测所有的样本都为正样本。经过以上的分析，我们可以断言，ROC曲线越接近左上角，该分类器的性能越好。

 下面我们来举个栗子，判断一下哪个分类器好一些：

 

A类样本90个	B 类样本10个	分类精度（分类正确占比）
分类器C1结果	A*90  (100%)	A*10 (0%)	90%
分类器C2结果	A*70 +  B*20 (78%)	A*5 + B*5  (50%)	75%

 

试样本中有A类样本90个，B类样本10个。分类器C1把所有的测试样本都分成了A类，分类器C2把A类的90个样本分对了70个，B类的10个样本分对了5个。则C1的分类精度为90%，C2的分类精度为75%，但直觉上，我们感觉C2更有用些。

       我们计算它的FPR和TRP，如下所示：

 

FPR	TPR
c1	10/10=1	90/90=1
c2	5/10=0.5	70/90=0.78

在ROC上可知，c2的分类更接近于左上角，它的分类能力要比c1好。

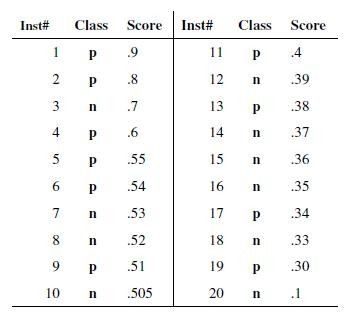
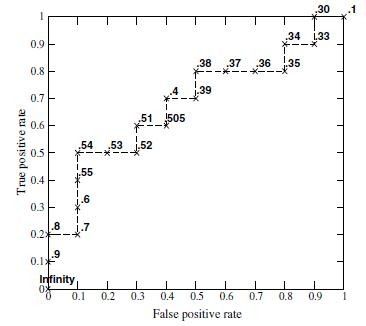
画roc曲线的时候，threshold采样点是有限的离散化点，其实就用score（什么是score？就是分类器给你的输入打的分），毕竟score是有限的。画曲线需要两个值TP/P和FP/N。P和N可以先扫描一遍找出来，后面不会变的。把score排一下序，从高到底，依次作为threshold（>=threshold的我们预测为p，其他为n）。

 

 

                                                                                                                  （1）data

 

                                                                                                                    

 

                                                                                                                            (2)ROC

当我们以0.6作为阈值，则在所有的10个正样本中，有3个是判断成了正样本，10个负样本中有一个被判断成了正样本，则TP/P=0.3，FP/N=0.1，所以它的坐标为（0.1，0.3）。

• 什么是AUC？

虽然ROC能够衡量模型的好坏，但是我们总是希望能够用一个数值来表达这个结果，于是AUC就产生了，它就是ROC的曲线下面的面积。

• 怎样计算AUC

       由于我们的测试样本是有限的。我们得到的AUC曲线必然是一个阶梯状的。因此，计算的AUC也就是这些阶梯下面的面积之和。这样，我们先把score排序(假设score越大，此样本属于正类的概率越大)，然后一边扫描就可以得到我们想要的AUC。当多个测试样本的score相等的时候，先累加正样本和先累加负样本的差异（先加TP往上走，还是FP往右走）。得到的不是曲线一个阶梯往上或者往右的延展，而是斜着向上形成一个梯形。此时，我们就需要计算这个梯形的面积。

python代码如下：

#!/usr/bin/python
import sys


#统计正负样本数
positive_vec = [0 for n in range(1000001)]
negative_vec = [0 for n in range(1000001)]

for line in sys.stdin:
    segs = line.strip('\n').split('\t')
    if len(segs) < 2:
        continue

    score = float(segs[0])
    flag = int(segs[1])

    label = flag
    if label > 0:
        label = 1
    val = score
    if val < 0.0 or val > 1.0:
        continue
    new_val = int(val * 1000000)
    if label > 0:
        positive_vec[new_val] += 1
    else:
        negative_vec[new_val] += 1

#计算梯形面积
sum_pos = 0
sum_neg = 0
area = 0
for i in range(1000000, -1, -1):
    area += (sum_pos * 2 + positive_vec[i]) * negative_vec[i] / 2
    sum_pos += positive_vec[i]
    sum_neg += negative_vec[i]

auc = float(area) / (sum_pos * sum_neg)

print str(auc)

使用方法：

假设上面的文件命名为auc.py输入数据为data.txt，格式为

score1,flag1

score2,flag2

...

scorek, flagk

其中0<=score=<1

flag=0 or 1(这是一个计算二分类的auc的方法，flag也可以取其它的二值 )

linux下使用命令，即为所求的auc

cat data.txt | python auc.py

不过，你也可以使用scikit-learn里面的计算auc的方法