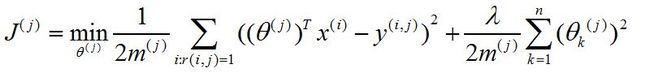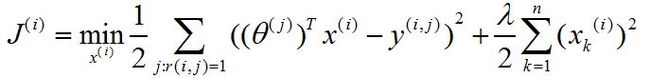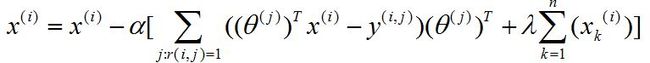协同过滤算法的基本原理与实现
众所周知,协同过滤(Collaboration Filtering)算法是推荐系统中最常用的一种算法。今天我们就以电影推荐为例,简要论述基本原理,最终给出实现的python代码。
1. 问题定义
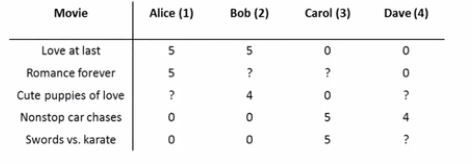
假设现有一个二维表,记录着每个用户对所看电影的评分情况,如下图所示:
从图中可知,该二维表记录着4个用户关于5部电影的评分情况,其中部分数据缺失。那么我们能否根据表格已有信息来对缺失值进行填充,实际意义就是能否根据用户喜好和电影特征来评估该用户对该电影的评分情况。因此,该问题需要解决两个小问题。一是用户喜好如何来衡量?二是电影特征如何确定?下面,我们将分别从这两个方面进行解释。
2. 已知电影特征
假设已知每部电影具有两个特征x1、x2,其中x1表示该电影浪漫的程度,x2表示该电影搞笑的程度。如果一部电影的特征表示为(1,0),那么就认为该电影是一部爱情浪漫片;如果特征表示为(0,1),那么就认为该电影是一部喜剧片;如果表示为(0.6,0.5),那么就认为该电影是一部爱情浪漫喜剧片。
如果现在已经通过手工标记,计算出所有电影的特征数据,那么我们就可以利用这些数据来学习每个用户的喜好了。由于电影特征x是二维的,用户喜好θ也应该是二维的。如果学习到Alice的用户喜好θ为(4.5,1),而《cute puppies of love》这部电影的特征为(0.9,0),那么就可以评估Alice对《cute puppies of love》的评分为4.05。该评分在现实中是合理的,Alice的用户喜好特征表明她喜欢爱情片,《cute puppies of love》的特征表明它是一部爱情片,因此评分也就较高。下面将给出数学化描述。
对于每一个用户而言,其优化目标为:
其中θj表示第j个用户的爱好特征,xi表示第i部电影的特征,y(i,j)表示第j个用户对第i部电影的评分,i:r(i,j)=1表示第j个用户对第i部电影是评了分的(不是缺失值),mj表示第j个用户评分电影的数目。右侧那一项为正则项,是防止过拟合的(之前算法经常见到,这里不再赘述)。由于左右两项具有mj,因此上式还可以写成:
接着,利用梯度下降更新θj
最终所求θj即为第j个用户的喜好特征。
3. 已知用户喜好
如果是已知用户喜好θ,那么我们就可以学习电影的特征x了。对于每一部电影,其优化函数为
接着,利用梯度下降更新xi
最终所求xi即为第i部电影的特征。
4. 两者结合
如果现在电影特征和用户喜好特征都未知,我们可以把上面两个目标函数结合起来进行优化。如下图所示
因此,可以得出如下协同过滤算法:
最终,我们可以得到用户喜好和电影特征。根据训练得到的这些参数,我们就可以预测那些缺失值了,然后就可以把那些预测的高分电影推荐给用户了。
5. 代码实现
import numpy as np
import pandas as pd
# 定义初始化参数函数
# 输入:特征数量、用户数量、产品数量
# 输出:用户特征初始矩阵、产品特征初始矩阵
def Initialize_Parameters(num_features, num_users, num_products):
user_matrix = np.random.rand(num_users, num_features)
product_matrix = np.random.rand(num_products, num_features)
return user_matrix, product_matrix
# 计算当前的代价函数
# 输入:当前的用户矩阵、产品矩阵、缺失的二维表、惩罚因子lambdaa
# 输出:当前代价
def get_cost(ori_data, user_matrix, product_matrix, lambdaa):
nan_index = np.isnan(ori_data) # 记录二维表中缺失的索引
ori_data[nan_index] = 0 # 把缺失值填充为0
predict_data = np.dot(user_matrix, product_matrix.T) # 计算预测的评分
temp = predict_data - ori_data # 计算两矩阵的差值
temp[nan_index] = 0 # 缺失值不算在代价里
cost = 0.5*np.sum(temp**2) + 0.5*lambdaa*(np.sum(user_matrix**2)+np.sum(product_matrix**2))# 计算平方
ori_data[nan_index] = np.nan # 恢复原数据
return cost
# 对用户特征进行偏导
# 输入:当前的用户矩阵、产品矩阵、缺失的二维表、惩罚因子lambdaa
# 输出:用户特征偏导矩阵
def get_user_derivatives(ori_data, user_matrix, product_matrix, lambdaa=1):
nan_index = np.isnan(ori_data) # 记录二维表中缺失的索引
ori_data[nan_index] = 0 # 把缺失值填充为0
predict_data = np.dot(user_matrix, product_matrix.T) # 计算预测的评分
temp = predict_data - ori_data # 计算两矩阵的差值
temp[nan_index] = 0 # 缺失值不算在代价里
ori_data[nan_index] = np.nan # 恢复原数据
num_user = user_matrix.shape[0] # 计算用户数目
feature_user = user_matrix.shape[1] # 计算特征数目
user_dervatives = np.random.rand(num_user, feature_user) # 声明用户特征偏导数矩阵
for i in range(num_user):
for j in range(feature_user):
user_dervatives[i][j] = np.dot(temp[i], product_matrix[:,j]) + lambdaa * user_matrix[i][j]
return user_dervatives
# 对产品特征进行偏导
# 输入:当前的用户矩阵、产品矩阵、缺失的二维表、惩罚因子lambdaa
# 输出:产品特征偏导矩阵
def get_product_derivatives(ori_data, user_matrix, product_matrix, lambdaa=1):
nan_index = np.isnan(ori_data) # 记录二维表中缺失的索引
ori_data[nan_index] = 0 # 把缺失值填充为0
predict_data = np.dot(user_matrix, product_matrix.T) # 计算预测的评分
temp = predict_data - ori_data # 计算两矩阵的差值
temp[nan_index] = 0 # 缺失值不算在代价里
ori_data[nan_index] = np.nan # 恢复原数据
num_product = product_matrix.shape[0] # 计算产品数目
feature_product = product_matrix.shape[1] # 计算特征数目
product_dervatives = np.random.rand(num_product, feature_product) # 声明产品特征偏导数矩阵
for i in range(num_product):
for j in range(feature_product):
product_dervatives[i][j] = np.dot(temp[:,i], user_matrix[:,j]) + lambdaa * product_matrix[i][j]
return product_dervatives
# 根据含有缺失值的二维表,学习相关参数
# 输入:含有缺失值的二维表、用户特征初始矩阵、产品特征初始矩阵、迭代次数、学习效率learning_rate、惩罚因子lambdaa
# 输出:最优用户特征矩阵、最优产品特征矩阵
def CF(ori_data, user_matrix, product_matrix, iterate_num=500, learning_rate=0.01, lambdaa=1):
for i in range(iterate_num):
cost = get_cost(ori_data, user_matrix, product_matrix, lambdaa) # 计算当前代价
user_derivatives = get_user_derivatives(ori_data, user_matrix, product_matrix, lambdaa) # 对用户特征求偏导
product_derivates = get_product_derivatives(ori_data, user_matrix, product_matrix, lambdaa) # 对产品特征求偏导
user_matrix = user_matrix - learning_rate * user_derivatives # 更新参数
product_matrix = product_matrix - learning_rate * product_derivates
print i,'th cost:', cost
return user_matrix, product_matrix
# 根据学习的参数,进行评估
# 输入:用户特征矩阵、产品特征矩阵
# 输出:不含缺失值的二维表
def Evaluate_Score(user_matrix, product_matrix):
return np.dot(user_matrix, product_matrix.T)
# 主函数
if __name__ == '__main__':
ori_data = np.array([[5,5,np.nan,0,0],[5,np.nan,4,0,0],[0,np.nan,0,5,5],[0,0,np.nan,4,np.nan]])
#user_matrix = np.array([[5,0.1],[5,0.1],[0.1,5],[0.1,5]])
#product_matrix = np.array([[0.9,0.1],[1.0,0.01],[0.99,0.01],[0.1,1.0],[0.1,0.9]])
user_matrix, product_matrix = Initialize_Parameters(2,ori_data.shape[0],ori_data.shape[1])
user_matrix, product_matrix = CF(ori_data, user_matrix, product_matrix, iterate_num=100, learning_rate=0.1, lambdaa=0)
score = Evaluate_Score(user_matrix, product_matrix)
print score6. 实验结果
以问题定义中的例子作为测试,经过100次迭代,最终预测的数据如下:
[[ 4.99997719e+00 4.99998362e+00 3.99998939e+00 2.70274725e-03 2.70273945e-03]
[ 4.99997832e+00 4.99998474e+00 3.99999029e+00 2.70274079e-03 2.70273299e-03]
[ -1.55079571e-07 -9.98770235e-08 -7.57981453e-08 5.00001356e+00 5.00000909e+00]
[ -1.18565589e-07 -7.44035873e-08 -5.62400915e-08 4.00000695e+00 4.00000337e+00]]
由此可见,预测的数据和原始数据很接近,因此该算法很有效。在测试的过程中发现一个问题:人为初始化参数有时无法进行梯度下降,我认为由于该算法的特殊性致使在前几次迭代中代价函数突然变大,从而无法继续迭代(有更好理解的欢迎评论交流)。在实验中,直接使用随机初始化参数即可。
附改进的代码(改用RMSprop梯度下降,原理)
import numpy as np
import pandas as pd
# 定义初始化参数函数
# 输入:特征数量、用户数量、产品数量
# 输出:用户特征初始矩阵、产品特征初始矩阵
def Initialize_Parameters(num_features, num_users, num_products):
user_matrix = np.random.rand(num_users, num_features)
product_matrix = np.random.rand(num_products, num_features)
return user_matrix, product_matrix
# 计算当前的代价函数
# 输入:当前的用户矩阵、产品矩阵、缺失的二维表、惩罚因子lambdaa
# 输出:当前代价
def get_cost(ori_data, user_matrix, product_matrix, lambdaa):
nan_index = np.isnan(ori_data) # 记录二维表中缺失的索引
ori_data[nan_index] = 0 # 把缺失值填充为0
predict_data = np.dot(user_matrix, product_matrix.T) # 计算预测的评分
temp = predict_data - ori_data # 计算两矩阵的差值
temp[nan_index] = 0 # 缺失值不算在代价里
cost = 0.5*np.sum(temp**2) + 0.5*lambdaa*(np.sum(user_matrix**2)+np.sum(product_matrix**2))# 计算平方
ori_data[nan_index] = np.nan # 恢复原数据
return cost
# 对用户特征进行偏导
# 输入:当前的用户矩阵、产品矩阵、缺失的二维表、惩罚因子lambdaa、加权平均参数
# 输出:用户特征偏导矩阵、加权平均矩阵
def get_user_derivatives(ori_data, user_matrix, product_matrix, weight_average_matrix, lambdaa=1, weight_average_para = 0):
nan_index = np.isnan(ori_data) # 记录二维表中缺失的索引
ori_data[nan_index] = 0 # 把缺失值填充为0
predict_data = np.dot(user_matrix, product_matrix.T) # 计算预测的评分
temp = predict_data - ori_data # 计算两矩阵的差值
temp[nan_index] = 0 # 缺失值不算在代价里
ori_data[nan_index] = np.nan # 恢复原数据
num_user = user_matrix.shape[0] # 计算用户数目
feature_user = user_matrix.shape[1] # 计算特征数目
user_dervatives = np.random.rand(num_user, feature_user) # 声明用户特征偏导数矩阵
for i in range(num_user):
for j in range(feature_user):
user_dervatives[i][j] = np.dot(temp[i], product_matrix[:,j]) + lambdaa * user_matrix[i][j]
weight_average_matrix = weight_average_para * weight_average_matrix + (1 - weight_average_para) * (user_dervatives ** 2) # 计算加权平均
user_dervatives = user_dervatives / (weight_average_matrix**0.5) # 计算变换的偏导
return user_dervatives, weight_average_matrix
# 对产品特征进行偏导
# 输入:当前的用户矩阵、产品矩阵、缺失的二维表、惩罚因子lambdaa
# 输出:产品特征偏导矩阵
def get_product_derivatives(ori_data, user_matrix, product_matrix, weight_average_matrix, lambdaa=1, weight_average_para=0):
nan_index = np.isnan(ori_data) # 记录二维表中缺失的索引
ori_data[nan_index] = 0 # 把缺失值填充为0
predict_data = np.dot(user_matrix, product_matrix.T) # 计算预测的评分
temp = predict_data - ori_data # 计算两矩阵的差值
temp[nan_index] = 0 # 缺失值不算在代价里
ori_data[nan_index] = np.nan # 恢复原数据
num_product = product_matrix.shape[0] # 计算产品数目
feature_product = product_matrix.shape[1] # 计算特征数目
product_dervatives = np.random.rand(num_product, feature_product) # 声明产品特征偏导数矩阵
for i in range(num_product):
for j in range(feature_product):
product_dervatives[i][j] = np.dot(temp[:,i], user_matrix[:,j]) + lambdaa * product_matrix[i][j]
weight_average_matrix = weight_average_para * weight_average_matrix + (1 - weight_average_para) * (product_dervatives ** 2) # 计算加权平均
product_dervatives = product_dervatives / (weight_average_matrix**0.5) # 计算变换的偏导
return product_dervatives, weight_average_matrix
# 根据含有缺失值的二维表,学习相关参数
# 输入:含有缺失值的二维表、用户特征初始矩阵、产品特征初始矩阵、迭代次数、学习效率learning_rate、惩罚因子lambdaa
# 输出:最优用户特征矩阵、最优产品特征矩阵
def CF(ori_data, user_matrix, product_matrix, iterate_num=500, learning_rate=0.01, lambdaa=1, weight_average_para=0.5):
user_weight_average_matrix = np.zeros(user_matrix.shape) # 初始化用户偏导加权平均为0
product_weight_average_matrix = np.zeros(product_matrix.shape) # 初始化产品偏导加权平均为0
for i in range(iterate_num):
cost = get_cost(ori_data, user_matrix, product_matrix, lambdaa) # 计算当前代价
user_derivatives, user_weight_average_matrix = get_user_derivatives(ori_data, user_matrix, product_matrix, user_weight_average_matrix, lambdaa, weight_average_para) # 对用户特征求偏导
product_derivates, product_weight_average_matrix = get_product_derivatives(ori_data, user_matrix, product_matrix, product_weight_average_matrix, lambdaa, weight_average_para) # 对产品特征求偏导
user_matrix = user_matrix - learning_rate * user_derivatives # 更新参数
product_matrix = product_matrix - learning_rate * product_derivates
print i,'th cost:', cost
return user_matrix, product_matrix
# 根据学习的参数,进行评估
# 输入:用户特征矩阵、产品特征矩阵
# 输出:不含缺失值的二维表
def Evaluate_Score(user_matrix, product_matrix):
return np.dot(user_matrix, product_matrix.T)
# 主函数
if __name__ == '__main__':
ori_data = pd.read_csv('cf_data.csv')
columns = ori_data.columns
ori_data = np.array(ori_data)
#ori_data = np.array([[5,5,np.nan,0,0],[5,np.nan,4,0,0],[0,np.nan,0,5,5],[0,0,np.nan,4,np.nan]])
user_matrix, product_matrix = Initialize_Parameters(20,ori_data.shape[0],ori_data.shape[1])
user_matrix, product_matrix = CF(ori_data, user_matrix, product_matrix, iterate_num=100, learning_rate=0.01, lambdaa=0)
score = Evaluate_Score(user_matrix, product_matrix)
predict_cf_data = pd.DataFrame(score, columns=columns)
predict_cf_data.to_csv('predict_cf_data.csv', index=False)