详解GAN代码之逐行解析GAN代码
训练数据集:手写数字识别
下载链接:https://pan.baidu.com/s/1d9jX5xLHd1x3DFChVCe3LQ 密码:ws28
在本篇博客中,笔者将逐行解析一下NIPS 2014的Generative Adversarial Networks(生成对抗网络,简称GAN)代码,该篇文章作为GAN系列的开山之作,在近3年吸引了无数学者的目光。在2017-2018年,各大计算机顶会中也都能看到各种GAN的身影。因此,本篇博客就来逐行解析一下使用GAN生成手写数字的代码。
在正式开始之前,笔者想说的是,如果要使得本篇博客对各位读者朋友的学习有帮助,请各位读者朋友们先熟悉生成对抗网络的基本原理。由于对于生成对抗网络的原理详解网络上的资源比较多,在本篇博客中笔者就不再对生成对抗网络的原理进行解释,而是给大家推荐一些对生成对抗网络原理进行了解的链接:
1. 直接进行论文阅读:https://arxiv.org/abs/1406.2661
2. 一篇通俗易懂,形象的GAN原理解释:一文看懂生成式对抗网络GANs:介绍指南及前景展望
3. 一篇比较详细的CSDN博文:生成式对抗网络GAN研究进展(二)——原始GAN
4. 知乎专栏上的文章:GAN原理学习笔记
如果对生成对抗网络原理已经熟稔的读者朋友,请自动忽略以上链接。并且,笔者以下放出的代码注释是参考了github上面的代码,链接https://github.com/wiseodd/generative-models
在这里笔者也想衷心感谢一下这位wiseodd大神,在他的generative-models下面的关于生成模型的代码非常全面,本文解析的代码路径是该工程下面的GAN/vanilla_gan/gan_tensorflow.py文件。笔者沿用了作者的代码,只是增加了模型保存与summary记录的少量代码,下面放出代码及注释:
import tensorflow as tf #导入tensorflow
from tensorflow.examples.tutorials.mnist import input_data #导入手写数字数据集
import numpy as np #导入numpy
import matplotlib.pyplot as plt #plt是绘图工具,在训练过程中用于输出可视化结果
import matplotlib.gridspec as gridspec #gridspec是图片排列工具,在训练过程中用于输出可视化结果
import os #导入os
def save(saver, sess, logdir, step): #保存模型的save函数
model_name = 'model' #模型名前缀
checkpoint_path = os.path.join(logdir, model_name) #保存路径
saver.save(sess, checkpoint_path, global_step=step) #保存模型
print('The checkpoint has been created.')
def xavier_init(size): #初始化参数时使用的xavier_init函数
in_dim = size[0]
xavier_stddev = 1. / tf.sqrt(in_dim / 2.) #初始化标准差
return tf.random_normal(shape=size, stddev=xavier_stddev) #返回初始化的结果
X = tf.placeholder(tf.float32, shape=[None, 784]) #X表示真的样本(即真实的手写数字)
D_W1 = tf.Variable(xavier_init([784, 128])) #表示使用xavier方式初始化的判别器的D_W1参数,是一个784行128列的矩阵
D_b1 = tf.Variable(tf.zeros(shape=[128])) #表示全零方式初始化的判别器的D_1参数,是一个长度为128的向量
D_W2 = tf.Variable(xavier_init([128, 1])) #表示使用xavier方式初始化的判别器的D_W2参数,是一个128行1列的矩阵
D_b2 = tf.Variable(tf.zeros(shape=[1])) ##表示全零方式初始化的判别器的D_1参数,是一个长度为1的向量
theta_D = [D_W1, D_W2, D_b1, D_b2] #theta_D表示判别器的可训练参数集合
Z = tf.placeholder(tf.float32, shape=[None, 100]) #Z表示生成器的输入(在这里是噪声),是一个N列100行的矩阵
G_W1 = tf.Variable(xavier_init([100, 128])) #表示使用xavier方式初始化的生成器的G_W1参数,是一个100行128列的矩阵
G_b1 = tf.Variable(tf.zeros(shape=[128])) #表示全零方式初始化的生成器的G_b1参数,是一个长度为128的向量
G_W2 = tf.Variable(xavier_init([128, 784])) #表示使用xavier方式初始化的生成器的G_W2参数,是一个128行784列的矩阵
G_b2 = tf.Variable(tf.zeros(shape=[784])) #表示全零方式初始化的生成器的G_b2参数,是一个长度为784的向量
theta_G = [G_W1, G_W2, G_b1, G_b2] #theta_G表示生成器的可训练参数集合
def sample_Z(m, n): #生成维度为[m, n]的随机噪声作为生成器G的输入
return np.random.uniform(-1., 1., size=[m, n])
def generator(z): #生成器,z的维度为[N, 100]
G_h1 = tf.nn.relu(tf.matmul(z, G_W1) + G_b1) #输入的随机噪声乘以G_W1矩阵加上偏置G_b1,G_h1维度为[N, 128]
G_log_prob = tf.matmul(G_h1, G_W2) + G_b2 #G_h1乘以G_W2矩阵加上偏置G_b2,G_log_prob维度为[N, 784]
G_prob = tf.nn.sigmoid(G_log_prob) #G_log_prob经过一个sigmoid函数,G_prob维度为[N, 784]
return G_prob #返回G_prob
def discriminator(x): #判别器,x的维度为[N, 784]
D_h1 = tf.nn.relu(tf.matmul(x, D_W1) + D_b1) #输入乘以D_W1矩阵加上偏置D_b1,D_h1维度为[N, 128]
D_logit = tf.matmul(D_h1, D_W2) + D_b2 #D_h1乘以D_W2矩阵加上偏置D_b2,D_logit维度为[N, 1]
D_prob = tf.nn.sigmoid(D_logit) #D_logit经过一个sigmoid函数,D_prob维度为[N, 1]
return D_prob, D_logit #返回D_prob, D_logit
def plot(samples): #保存图片时使用的plot函数
fig = plt.figure(figsize=(4, 4)) #初始化一个4行4列包含16张子图像的图片
gs = gridspec.GridSpec(4, 4) #调整子图的位置
gs.update(wspace=0.05, hspace=0.05) #置子图间的间距
for i, sample in enumerate(samples): #依次将16张子图填充进需要保存的图像
ax = plt.subplot(gs[i])
plt.axis('off')
ax.set_xticklabels([])
ax.set_yticklabels([])
ax.set_aspect('equal')
plt.imshow(sample.reshape(28, 28), cmap='Greys_r')
return fig
G_sample = generator(Z) #取得生成器的生成结果
D_real, D_logit_real = discriminator(X) #取得判别器判别的真实手写数字的结果
D_fake, D_logit_fake = discriminator(G_sample) #取得判别器判别的生成的手写数字的结果
D_loss_real = tf.reduce_mean(tf.nn.sigmoid_cross_entropy_with_logits(logits=D_logit_real, labels=tf.ones_like(D_logit_real))) #对判别器对真实样本的判别结果计算误差(将结果与1比较)
D_loss_fake = tf.reduce_mean(tf.nn.sigmoid_cross_entropy_with_logits(logits=D_logit_fake, labels=tf.zeros_like(D_logit_fake))) #对判别器对虚假样本(即生成器生成的手写数字)的判别结果计算误差(将结果与0比较)
D_loss = D_loss_real + D_loss_fake #判别器的误差
G_loss = tf.reduce_mean(tf.nn.sigmoid_cross_entropy_with_logits(logits=D_logit_fake, labels=tf.ones_like(D_logit_fake))) #生成器的误差(将判别器返回的对虚假样本的判别结果与1比较)
dreal_loss_sum = tf.summary.scalar("dreal_loss", D_loss_real) #记录判别器判别真实样本的误差
dfake_loss_sum = tf.summary.scalar("dfake_loss", D_loss_fake) #记录判别器判别虚假样本的误差
d_loss_sum = tf.summary.scalar("d_loss", D_loss) #记录判别器的误差
g_loss_sum = tf.summary.scalar("g_loss", G_loss) #记录生成器的误差
summary_writer = tf.summary.FileWriter('snapshots/', graph=tf.get_default_graph()) #日志记录器
D_solver = tf.train.AdamOptimizer().minimize(D_loss, var_list=theta_D) #判别器的训练器
G_solver = tf.train.AdamOptimizer().minimize(G_loss, var_list=theta_G) #生成器的训练器
mb_size = 128 #训练的batch_size
Z_dim = 100 #生成器输入的随机噪声的列的维度
mnist = input_data.read_data_sets('../../MNIST_data', one_hot=True) #mnist是手写数字数据集
sess = tf.Session() #会话层
sess.run(tf.global_variables_initializer()) #初始化所有可训练参数
if not os.path.exists('out/'): #初始化训练过程中的可视化结果的输出文件夹
os.makedirs('out/')
if not os.path.exists('snapshots/'): #初始化训练过程中的模型保存文件夹
os.makedirs('snapshots/')
saver = tf.train.Saver(var_list=tf.global_variables(), max_to_keep=50) #模型的保存器
i = 0 #训练过程中保存的可视化结果的索引
for it in range(1000000): #训练100万次
if it % 1000 == 0: #每训练1000次就保存一下结果
samples = sess.run(G_sample, feed_dict={Z: sample_Z(16, Z_dim)})
fig = plot(samples) #通过plot函数生成可视化结果
plt.savefig('out/{}.png'.format(str(i).zfill(3)), bbox_inches='tight') #保存可视化结果
i += 1
plt.close(fig)
X_mb, _ = mnist.train.next_batch(mb_size) #得到训练一个batch所需的真实手写数字(作为判别器的输入)
#下面是得到训练一次的结果,通过sess来run出来
_, D_loss_curr, dreal_loss_sum_value, dfake_loss_sum_value, d_loss_sum_value = sess.run([D_solver, D_loss, dreal_loss_sum, dfake_loss_sum, d_loss_sum], feed_dict={X: X_mb, Z: sample_Z(mb_size, Z_dim)})
_, G_loss_curr, g_loss_sum_value = sess.run([G_solver, G_loss, g_loss_sum], feed_dict={Z: sample_Z(mb_size, Z_dim)})
if it%100 ==0: #每过100次记录一下日志,可以通过tensorboard查看
summary_writer.add_summary(dreal_loss_sum_value, it)
summary_writer.add_summary(dfake_loss_sum_value, it)
summary_writer.add_summary(d_loss_sum_value, it)
summary_writer.add_summary(g_loss_sum_value, it)
if it % 1000 == 0: #每训练1000次输出一下结果
save(saver, sess, 'snapshots/', it)
print('Iter: {}'.format(it))
print('D loss: {:.4}'. format(D_loss_curr))
print('G_loss: {:.4}'.format(G_loss_curr))
print()在上面的代码中,各位读者朋友可以看到,生成器与判别器都是使用多层感知机实现的(没有使用卷积神经网络)。生成器的输入是随机噪声,生成的是手写数字,生成器与判别器均使用Adam优化器进行训练并训练100w次。
在上面的代码中,笔者添加了各种summary保存了训练中的误差,结果如下所示。
判别器判别真实样本的误差变化:
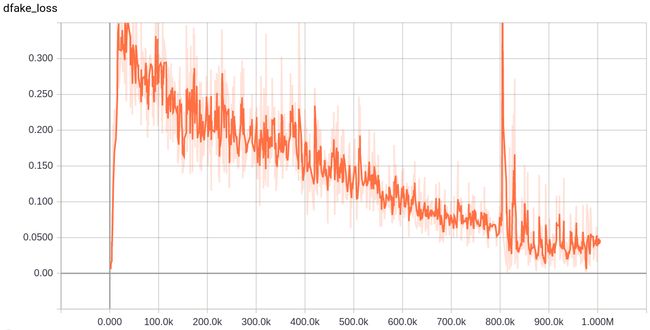
判别器判别虚假样本(即生成器G生成的手写数字)的误差变化:
判别器的误差变化(上面两者之和):
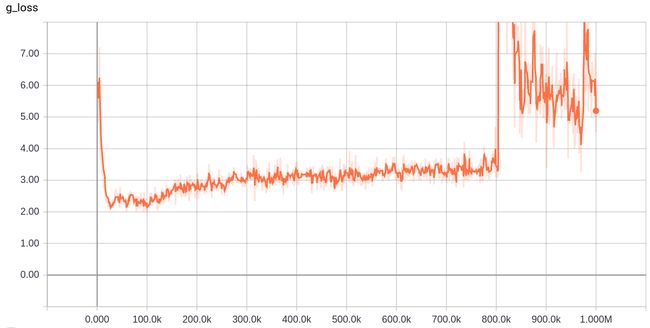
生成器的误差变化:
下面是训练过程中输出的可视化结果,笔者选择了一些,大家可以看到,生成器输出结果最开始非常糟糕,但是随着训练的进行到训练中期输出效果越来越好:
训练2k次的输出:
训练6k次的输出:
训练4.2w次的输出
训练14.4w次的输出:
训练24.4w次的输出:
训练31.6w次的输出:
在训练的后期(训练80w次之后),大家从生成器的误差曲线可以看出,生成器的误差陡增,生成效果也相应变差了(如下图所示),这是生成器与判别器失衡的结果。
训练85.7w次的输出:
训练93.6w次的输出:
训练97.2w次的输出:
到这里,生成对抗网络的代码讲解就接近尾声了,衷心希望笔者的本篇博客对大家有帮助!
欢迎阅读笔者后续博客,各位读者朋友的支持与鼓励是我最大的动力!
written by jiong
日出入安穷?时世不与人同。
故春非我春,夏非我夏,秋非我秋,
冬,亦非我冬。