【无人驾驶规划】BOSS无人车规划算法

1、boss运动规划结构

boss无人车运动规划结构如图所示

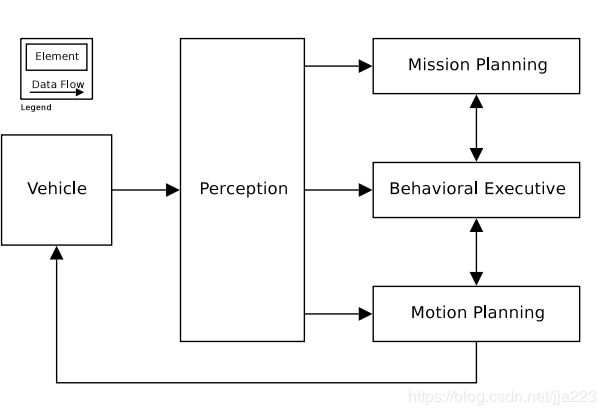
其中任务规划的任务就是全局的路由寻径；
行为规划的任务是结合全局路径信息和当前交通、障碍物等情况，给运动规划模块输入一系列的局部目标，比如说沿着一条车道运动到某个位置或者运动到一个特定的位姿或者停车位，同时也可以给运动规划模块输入特定的最大速度以及加减速指令等等；
运动规划接收行为规划的目标，生成安全运动轨迹。
运动规划分为两种模式，一种是on-road模式就是正常上路模式，另一种是unstructured driving比如停车场。
运动规划的流程：
1、根据给定的运动目标，规划一条路径；
2、生成一系列的轨迹去跟踪这条路径，这里涉及到轨迹生成；
3、从生成的轨迹中选取最优轨迹。
注：路径生成算法、轨迹评价函数等在不同场景下是不同的。

2、轨迹生成

boss采用模型预测的轨迹生成算法生成轨迹，从当前状态到目标状态。
模型预测轨迹生成算法论文：Howard, T., Kelly, A.: Optimal rough terrain trajectory generation for wheeled mobile robots.International Journal of Robotics Research 26(2), 141–166 (2007)
模型预测算法可以表示为：

其中x表示车辆状态，包括位置，朝向，曲率，速度；$u(p,x)$表示参数化的控制输入。

2.1、状态约束

车辆导航考虑三个约束，位置(x,y)和朝向($\theta$)，约束方程为：

其中$X_C$为目标状态，$X_F(p,x)$表示根据模型和控制策略预测出来的车辆状态，$X_I$为当前状态，$C(x,p)$表示目标状态和当前轨迹之差，也就是目标函数。理想状态下$C(x,p)$为0。

2.2、车辆模型

Ackermann转向模型

2.3、控制参数化

车辆控制分为两部分，一部分是基于时间线形速度方程，还有一部分是基于路程的曲率方程

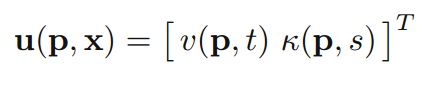
线形速度配置有几种模式如图所示

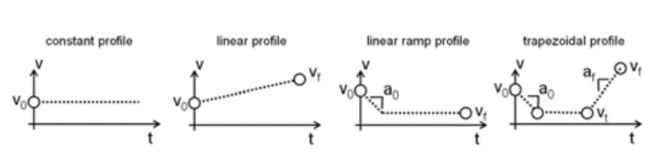
每个速度配置方式都有几个独立的参数 V0 Vf a0等，还有时间（t0，tf），这些就成为了参数p的成员。
曲率配置方式如图所示

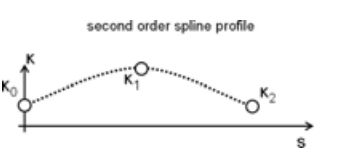
包括了三个参数k0 k1 k2 和轨迹长度Sf，用二次函数来拟合曲率配置。
对于速度配置来说参数都是完全确定了的，为了曲率平滑一点将曲率配置的k0也固定死，因此只剩下三个自由参数

当然也可以不固定$k_0$。
特定速度配置下的总时间可以计算得到。

2.4、初始化轨迹

通过离线表格得到初始化轨迹，目的是为了增加优化速度。
离线表格生成方式
1、将初始和最终状态进行离散，5个维度的离散；
2、均匀采样所有可取的控制参数（$k_1$，$k_2$，$s$）并根据模型得到相应的轨迹；
3、每个5D离散状态找到2中最终点离得最近的轨迹，离得最近是$(x,y,\theta )$三维离得最近；
4、对轨迹参数进行优化 （雅可比）
5D包括relative initial and terminal position ($\delta$x, $\delta$y), relative heading ($\delta$θ), initial curvature (${\kappa }_i$), and constant velocities ($v$)
个人认为5D中前面三个是车辆三个状态约束，用来判断模型轨迹与目标位置的距离；$({\kappa }_i)$就是上文中说到的为了平滑轨迹而定死的$k_0$，$v$只取两个值，一正一负，用来判断车辆前进方向，与lattice planner论文中的4D lattice的$v$是一致的。

初始化就根据行为规划中输出的目标位置$(x,y,\theta )$去距离最近的几条轨迹的对应的控制参数的插值结果$(k1,k2,Sf)$，这样初始化的轨迹比较接近最优轨迹，优化速度快。

2.5、轨迹优化

轨迹优化采用雅可比矩阵方法。控制参数p的收敛方向计算如图，优化目标使得目标函数C(x,p)趋向0：

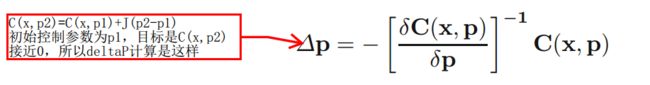
优化结束判断条件是目标函数小于某个值或者发散，发散的话取最接近的那一组参数，如果差值可以接受就取这组参数的轨迹。
针对一个目标点的在线轨迹生成方式如图所示：

初始轨迹的参数由几组离线轨迹插值得到。

3、on-road模式规划

3.1、路径生成

对于on-road模式来说，运动目标是road lane上的一个位置，因此取车道中心线作为目标路径。

3.2、轨迹生成

1、从车道中心线路径分离处一系列的局部目标点，这些局部目标点纵向方向与路径目标点一致，横向方向与路径目标点有偏离；
2、对于每一个局部目标点，都会生成两种轨迹：平滑轨迹(smooth trajectory)和陡峭轨迹(sharp trajectory)，smooth trajectory就是上文中的固定$k_0$，sharp trajectory的$k_0$与与smooth trajectory的会有所偏差，sharp trajectory是为了对突然出现的障碍物进行快速相应。

3.3、轨迹速度配置

轨迹速度配置从上文中的几种中挑选，根据当前跟随距离的最大速度、路段速度限制、路径曲率的最大速度、目标点速度（stopline）等。
通常，选择能够始终最大化车辆速度的配置。 因此，通常使用线性斜坡配置，其斜坡速度等于可能的最大速度，并且线性分量对应于可能的最大加速度。如果车辆正在慢慢接近停车线（或停在停车线以外），则采用梯形配置，以便车辆可以到达停车很快就顺利停下来了。
当初始速度配置会造成endpoint较大误差时需要考虑多个速度配置方式，这是由于速度配置与轨迹曲率变化率无法匹配的情况出现。在这种情况下，更小的速度和更小的加速度配置会被考虑直到一个有效的轨迹被发现或者新增加的速度配置达到上限。

3.4、轨迹评价

所有的轨迹会根据判断方式进行评价，其中涉及的判断条件有：与障碍物的距离、与中心线的距离、平滑度、最终点误差(endpoint error)以及轨迹的速度等。由于轨迹都是通过模型预测生成的，所以都是可以被执行的。
与其他车辆的避障：会预测其他车辆的轨迹并进行碰撞检测。

更详细的碰撞检测方式论文：Ferguson, D., Darms, M., Urmson, C., Kolski, S.: Detection, Prediction, and Avoidance of Dynamic Obstacles in Urban Environments. In: Proceedings of the IEEE Intelligent Vehicles Symposium, IV (2008)
动态障碍物碰撞检测方式：
1、根据车辆规划轨迹以及避碰车辆预测轨迹，为自己车辆和避碰车辆分别画一个大的矩形区域，如果两个矩形区域不叠加则不碰撞，若叠加则需要进一步检测；
2、若1判断由重叠区域，则将轨迹时间离散化，每一个时间节点给车辆画一个膨胀圆，检测每个时间节点膨胀圆是否发生碰撞，若不碰撞则判断不会碰撞，若碰撞需要进一步检测；
3、为每个时间节点画精确的车辆模型(也就是矩形)，检测举行会不会放生碰撞，若碰撞最最终判断会发生碰撞，删去这条轨迹。
这样做的好处是多边形的碰撞检测比较复杂，用一个大的区域和圆先进行粗略判断。如图

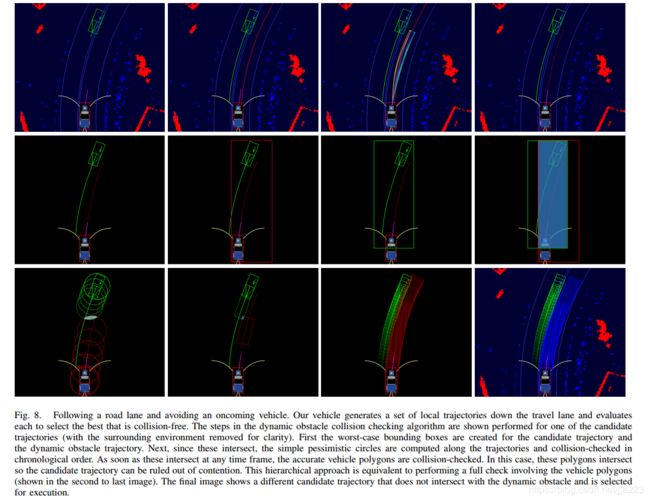
3.5、换车道

与正常形式是类似的，只不过desired lane换了。同时由于有可能无法马上换车道，一条沿着原车道的轨迹也会生成。

3.6、U—turns

1、根据道路情况，有一次性掉头(a single forwards segment)、三点式掉头(a three-point turn)，如果这两个都不行，则需要调用lattice planner进行规划；
2、与上文相同，以该路径为基础生成轨迹。

3.7、保护性驾驶

如果其他车辆由异常驾驶情况(逆行)，则需要采取保护性驾驶行为，行为规划会决策让车辆往道路右边开，并停止。这与换车道是类似的，只不过目标点不一样。

5.8、异常检测与恢复

如果正常规划无法规划出轨迹，则会调用lattice planner。

6、非结构性规划

采用4D-lattice planner，4D包括$(x,y,\theta ,v)$。当前状态的下一个可行节点离线计算好，采用Anytime D*算法进行搜索，启发函数有两个，两者取最大：不考虑障碍物只考虑车辆约束（离线、考虑障碍物并用2D grid-based Dijkstra’s search（在线）。
Anytime D*： Likhachev, M., Ferguson, D., Gordon, G., Stentz, A., Thrun, S.: Anytime Dynamic A*: An Anytime, Replanning Algorithm. In: Proceedings of the International Conference on Automated Planning and Scheduling, ICAPS (2005)
详细的lattice planner： Likhachev, M., Ferguson, D.: Planning Dynamically Feasible Long Range Maneuvers for Autonomous Vehicles. In: Proceedings of Robotics: Science and Systems, RSS (2008)
Ferguson, D., Likhachev, M.: Efficiently using cost maps for planning complex maneuvers. In: Proceedings of the Workshop on Planning with Cost Maps, IEEE International Conference on Robotics and Automation (2008)
第一个启发函数离线计算： Knepper, R., Kelly, A.: High performance state lattice planning using heuristic look-up tables. In: Proceedings of the IEEE International Conference on Intelligent Robots and
Systems, IROS (2006)

6.1、复杂路径的轨迹生成

与on-road中不同，轨迹最终都要回到路径上去，因此轨迹生成可以分为两段，一段与路径由偏离，第二段回到路径中去，为了充分避障。

6.2、Lattice planner

论文： Likhachev, M., Ferguson, D.: Planning Dynamically Feasible Long Range Maneuvers for Autonomous Vehicles. In: Proceedings of Robotics: Science and Systems, RSS (2008)
Lattice planner中几个关键因素：
1、采用图搜索算法，Anytime D*算法，给启发函数乘上一个膨胀因子$ϵ>1$，目的是快速得到一个次优路径，然后$ϵ$随时间减小，利用前面的次优路径进行重规划，如何利用需要再看论文。D*算法用来解决环境更新问题，也需要再看论文。这个算法的好处是能够解决搜索时间约束；
2、图搜索节点为4D，$(x,y,\theta ,v)$，其中前三个为车辆位姿，$v$只取两个值：最大前进速度和最大后退速度，只是用来判断车辆前进方向；
3、图搜索边考虑车辆模型离线计算好，计算方式参考以下论文，并且使用上文中轨迹生成模型将控制参数(先查表找最近，再优化)与lattice节点对应起来，与论文中的差别在于加入了不同长度的直线段，并且使用了Multi-resolution Lattice，在初始点和终止点附近取得密一些，低分辨率是高分辨率的子集；
论文：M. Pivtoraiko and A. Kelly, “Generating near minimal spanning control sets for constrained motion planning in discrete state spaces,” in Proceedings of the IEEE International Conference on Intelligent Robots and Systems (IROS), 2005.

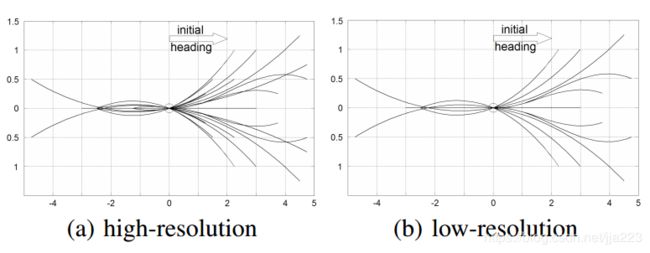
4、启发函数，启发函数有两个，一个是考虑车辆模型不考虑障碍物（离线计算），一个是考虑障碍物不考虑车辆模型（在线计算）。后者采用2D Dijkstra算法，从车辆位置开始搜索，这样就可以计算出大部分位置到车辆位置的无碰撞路径。而AD*从终点位置开始搜索，这样就可以利用Dijkstra算法的g值作为启发函数，非常巧妙。采用Dijkstra暴力搜索就是为了覆盖的位置多一些。最终启发函数取两个启发函数中大的那个，也就是惩罚值大一些。
5、代价函数，代价函数做了两个优化。
（1）每一个动作actions将会覆盖的栅格离线计算好；
（2）从感知得到的地图中衍生出两幅地图，第一幅对障碍物根据车辆的内圆进行碰撞，第二幅对障碍物根据车辆的外圆进行膨胀。如果路径（action）与第一幅图发生碰撞，则一定会碰撞；如果与第二幅图不发生碰撞，则一定不会碰撞。如果路径（action）不属于，则需要跟感知地图进行进一步检测。

注：若要使用lattice planner还需要搞清楚AD*和离线生成边的方式。个人认为需要注意节点爆炸问题，节点之间差别最好大一点防止节点无限扩展，之前泊车系统的路径仿真应该还有问题。