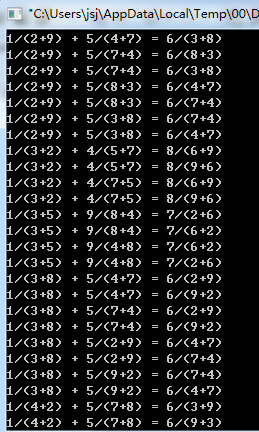
1-9九个数字组合成三个分数
#include
#include
usingnamespace std;
structmyarr
{
inta[9];
structmyarr *next;
}mya,myall;
staticvoid showArr(int arr[], int len = 9)
{
cout<
cout<<"/";
cout<<"("<
cout<<"+ ";
cout<
cout<<"/";
cout<<"("<
cout<<"= ";
cout<
cout<<"/";
cout<<"("<
cout<
}
staticint Max(int a,int b,int c)
{
intmax=a>b?a:b;
returnmax=max>c?max:c;
}
//求最大公倍数
staticint MixCMul_1(int a, int b,int c)
{
intmax = Max(a,b,c);
while(true)
{
if(max%a == 0 && max%b == 0 && max%c == 0)
break;
max++;
}
returnmax;
}
staticvoid printmol1(int arr[], int len = 9)
{
intmol[3] = {0}; // 分子
intDen[3] = {0}; // 分母
//按倍数扩充后的
inttemmol[3] = {0}; // 分子
intMixCMul1=0, MixCMul2=0;
for(size_t i = 0; i < 3; i++)
{
mol[i]= arr[i*3];
Den[i]= arr[i*3+1] + arr[i*3+2];
}
//计算第一和第二个分数分母的最小公倍数,同时扩大分子
MixCMul1 = MixCMul_1(Den[0], Den[1],Den[2]);
temmol[0]= MixCMul1/Den[0] * mol[0];
temmol[1]= MixCMul1/Den[1] * mol[1];
temmol[2]= MixCMul1/Den[2] * mol[2];
//分子的比较,去除分子比分母大的算式,
if((temmol[2] == (temmol[0]+temmol[1])) && Den[0]>mol[0] &&Den[1]>mol[1] && Den[2]>mol[2])
{
showArr(arr);
}
}
//数组的各种排列
staticvoid Grial1(int a[], int n,int m)
{
if(n == m)
{
printmol1(a);
}
else
{
for(int i = n; i < m; i++)
{
std::swap(a[i],a[n]);
Grial1(a,n+1,m);
std::swap(a[i],a[n]);
}
}
}
/****************************************************************************************/
voidget(int a[],int n)
{
int*p=(int *)malloc(sizeof(int)*n);
int*q=p,*head=p;
for(int i = 0; i < 9; i++)
{
p[i]=a[i];
}
for(intj=0;j
{
cout<
}
}
intmain(int argc, char* argv[])
{
#defineARR_NUM 9
intarr[ARR_NUM] = {1, 2, 3, 4, 5, 6, 7, 8, 9};
Grial1(arr,0,ARR_NUM);
return0;
}