切线空间(Tangent Space)
-
-
- 1. 线性变换
- 2. 切线空间(坐标系)
- 2.1 切线空间的构成
- 2.2 切线空间中光照计算及其弊端
- Reference
-
1. 线性变换
在掌握切线空间之前我们先来简单了解线性变换与向量空间、矩阵的关系。
什么是线性变换?
简单来说,线性变换就是一种映射关系,我们来看看线性代数对线性方程组的描述——线性方程组是由一个或者几个包含相同变量 x1,x2,x3,...,xn x 1 , x 2 , x 3 , . . . , x n 的线性方程组成的,如:
假设我们有 m m (本文假设 m=n m = n ) 个方程组,以矩阵形式表达该方程组如下:
A A 是一个 m∗n m ∗ n 的方块矩阵( m=n m = n ), x=(x1,x2,...,xn) x = ( x 1 , x 2 , . . . , x n ) 是一个 n n 维向量, b=(b1,b2,...,bn) b = ( b 1 , b 2 , . . . , b n ) 是一个 m m 维向量。 那么如何理解线性方程组的矩阵表达式 (2) ( 2 ) 呢?
首先,我们将 A A 看成是由 n n 个列向量组成的:
那么公式 (2) ( 2 ) 可以表示为:
列向量的线性组合是 Rm R m 向量空间的子空间,称为矩阵的列空间(矩阵行向量的线性组合生成在 Rn R n 向量空间的子空间,称为矩阵的行空间)。 如果我们把 A A 看成是看成是 Rn R n 到 Rm R m 的线性变换,则矩阵列空间是线性变换的 像,向量 x x 是该线性变换的 原像,我们把向量 x x 看成是 原坐标系(以矩阵 A A 列向量的最大线性无关组为一组基底的坐标系)下描述的一个向量,那么向量 b b 则是 目标坐标系(以矩阵行向量最大线性无关组为一组基底的坐标系)下描述的一个向量,向量 b b 的每个分量值都可以看成是向量 b b 在目标坐标系对于每一个坐标基的投影长度([ Wiki——行空间与列空间]),因此,向量 x x 和 b b 是同一个向量在不同坐标系下的不同描述。 怎么理解向量 b b 的分量是相对目标坐标系坐标基的投影长度呢?
我们来看看两个向量 v1 v 1 和 v2 v 2 ,现在求 v1 v 1 在 v2 v 2 上的投影,看下图((;′⌒`)):
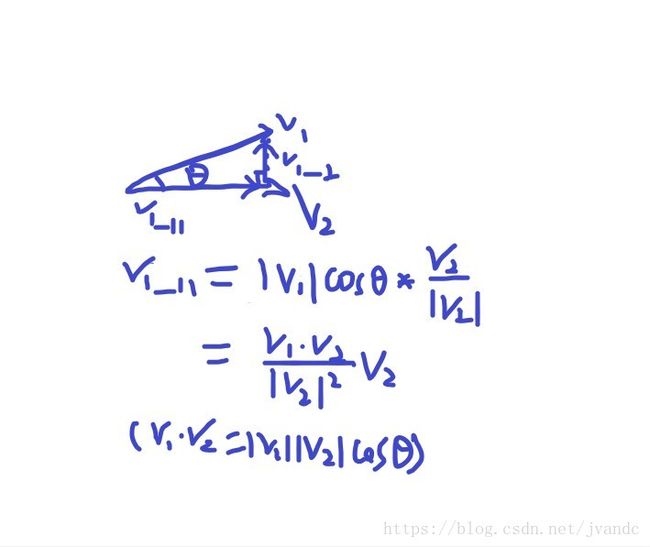
向量 v1=v1proj+v1perp v 1 = v 1 p r o j + v 1 p e r p , v1proj v 1 p r o j 表示向量 v1 v 1 平行于 v2 v 2 的投影向量,从上图中可以看出,如果向量 v2 v 2 是一个单位向量,那么向量 v1 v 1 关于 v2 v 2 的投影长度刚好等于两者点积 dot(v1,v2) d o t ( v 1 , v 2 ) ,由此结合公式 (1) ( 1 ) 的线性方程组表达式,向量 b b 的分量的值也恰好等于矩阵 A A 行向量与向量 x x 的点积,假设 A A 行向量为单位向量,那么 x x 的每一个分量则表示其相对于以矩阵 A A 行向量构造的坐标系的每一个坐标基的投影长度。
2. 切线空间(坐标系)
切线空间有时也称为纹理空间,切线空间最常见的应用场景是使用法线纹理进行光照计算,而法线纹理其内容有两种表达形式,一种是基于模型空间的,另一种就是基于切线空间的;此外,纹理映射的基本技术(计算纹理坐标)正是基于纹理空间定义的纹理函数[10],它将 2D 图片投影到 3D 模型的表面。(计算机图形学中一般没有区分切线空间和纹理空间。)
2.1 切线空间的构成
切线空间(切线坐标系)通常简称为 TBN 坐标系(Tangent——切线,Binormal——副法线或者Bitangent,Norma——法线),通过上一节“线性变换”我们知道一个 n 维度“坐标系”的构成实际上需要 n 个正交基(也就是 n 个线性无关向量组),下面详细分析 TBN 坐标系,如何计算这三个基向量。
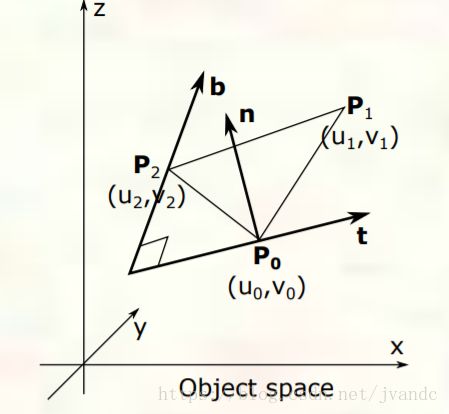
TBN 坐标系建立在模型表面(Surface)之上,N 表示模型表面的法线,T 则是与该法线垂直的切线(理论上我们可以选择任意一条与 N 垂直的切线),B 是与 T、B 都垂直的副法线。假设现在有一个三角形,其顶点分别是 P0、P1、P2 P 0 、 P 1 、 P 2 ,假设表面法线向量为 N N ,现在要求取 T T 、 B B ,
如上图使用顶点位置坐标随纹理坐标(UV)的变化定义 T T 和 B B ,它们的计算如下:
计算出来的 T T 、 B B 、 N N 有可能不是正交的,因此,还需要对这三个向量正交化处理(施密特正交化):
最终得到的 N N 、 T′ T ′ 、 B′ B ′ 就是切线空间的三个基向量。
模型空间(Object Space)转换切线做空间的矩阵表示:
切线空间转到模型空间(Object Space)的矩阵表示:
2.2 切线空间中光照计算及其弊端
- 切线空间光照计算。
如果在 WorldSpace 计算光照,那么表面法向量需要变换到世界坐标空间,而每一个表面的法向量都有可能不同,导致矩阵变换计算消耗较大,相对而言,在切线空间中计算光照,只需要把光源方向(和视线方向)变换到切线空间,矩阵计算相对较少。(这里顺便提一句,理论上我们可以认为 GPU 是一个一个像素进行处理的,而实际上 GPU 执行的最小单位并不是单个像素,GPU 以像素为单位将其执行指令转换成 Thread,而且为方便硬件吞吐,若干 Thread 又组合成 Thread 块——称为CTA,它便对应了硬件可执行的最小处理单位。) - 弊端
Reference
[1] 线性代数及其应用.
[2] Wiki——行空间与列空间.
[3] 切线空间
[4] Messing With Tangent Space
[5] CryEngine——Tangent Space And Normal Mapping
[6] Texture Mapping
[7] UVMapping
[8] Wiki——法线贴图
[9] 计算机图形学 OpenGL 第三版 P365
[10] 为什么要有切线空间