用回溯法解决图着色问题

海南师范大学学生狗一枚，最近老师要求算法设计论文一篇，，心累，，，耗时一周终于弄出来，，，就存在这里了，，以后留着用。

 

【摘要】图着色问题（Graph Coloring Problem, GCP）　又称着色问题，是最著名的NP-完全问题之一。其数学定义为：给定一个无向图G=（V, E），其中V为顶点集合，E为边集合，图着色问题即为将V分为K个颜色组，每个组形成一个独立集，即其中没有相邻的顶点。其优化版本是希望获得最小的K值。

回溯法（探索与回溯法）是一种选优搜索法，又称为试探法，按选优条件向前搜索，以达到目标。但当探索到某一步时，发现原先选择并不优或达不到目标，就退回一步重新选择，这种走不通就退回再走的技术为回溯法，而满足回溯条件的某个状态的点称为“回溯点”。

 

【关键词】算法设计、回溯法、图着色问题

一、     问题描述与思想概述

（1）、问题的提出

       给定无向连通图G和m种不同的颜色。用这些颜色为图G的各顶点着色，每个顶点着一种颜色。是否有一种着色法使G中每条边的2个顶点着不同颜色。这个问题是图的m可着色判定问题。若一个图最少需要m种颜色才能使图中每条边连接的2个顶点着不同颜色，则称这个数m为该图的色数。求一个图的色数m的问题称为图的m可着色优化问题。

输入：无向图,m

输出：如果能，则输出方案

 

四色问题是m图着色问题的一个特例，根据四色原理，证明平面或球面上的任何地图的所有区域都至多可用四种颜色来着色，并使任何两个有一段公共边界的相邻区域没有相同的颜色。这个问题可转换成对一平面图的４－着色判定问题(平面图是一个能画于平面上而边无任何交叉的图)。将地图的每个区域变成一个结点，若两个区域相邻，则相应的结点用一条边连接起来。多年来，虽然已证明用5种颜色足以对任一幅地图着色，但是一直找不到一定要求多于4种颜色的地图。直到1976年这个问题才由爱普尔，黑肯和考西利用电子计算机的帮助得以解决。他们证明了4种颜色足以对任何地图着色。

（2）、问题的处理

如果把每一个区域收缩为一个顶点，把相邻两个区域用一条边相连接，就可以把一个区域图抽象为一个平面图。

用m种颜色为图中的每个顶点着色，要求每个顶点着一种颜色，并使相邻两顶点之间有着不同的颜色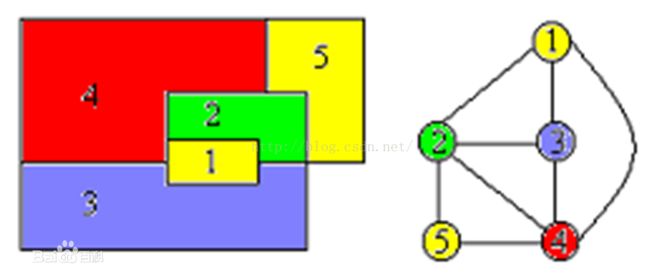

抽象地图及其相应的平面图

 

可以通过回溯的方法，不断的为每一个节点着色，在前面n-1个节点都合法的着色之后，开始对第n个节点进行着色，这时候枚举可用的m个颜色，通过和第n个节点相邻的节点的颜色，来判断这个颜色是否合法，如果找到那么一种颜色使得第n个节点能够着色，那么说明m种颜色的方案是可行的。

（3）、回溯法介绍及其基本思想

回溯法有“通用的解题法”之称。用它可以系统的搜索一个问题的所有解或任一解。是一个既带有系统性又带有跳跃性的搜索算法。

在包含问题的所有解的解空间树中，按照深度优先搜索的策略，从根结点出发深度探索解空间树。当探索到某一结点时，要先判断该结点是否包含问题的解，如果包含，就从该结点出发继续探索下去，如果该结点不包含问题的解，则逐层向其祖先结点回溯。（其实回溯法就是对隐式图的深度优先搜索算法）。若用回溯法求问题的所有解时，要回溯到根，且根结点的所有可行的子树都要已被搜索遍才结束。而若使用回溯法求任一个解时，只要搜索到问题的一个解就可以结束。

（4）、回溯法解题步骤

在用回溯法搜索解空间树时，通常采用两种策略来避免无效搜索，提高回溯法的搜索效率。其一是用约束函数在扩展结点处剪去不满足约束的子树；其二是用限界函数剪去不能得到最优解得子树。这两类函数统称剪枝函数。

运用回溯法解题通常包含以下三个步骤：

（1）针对所给问题，定义问题的解空间

（2）确定易于搜索的空间结构

（3）以深度优先的方式搜索解空间，并且在搜索过程中用剪枝函数避免无效搜索。

二、算法设计过程（解问题过程）

（1）、解题思路

我们讨论一般连通图的可着色问题，而不只是平面图。给定一个平面图G=（V，E）和M种颜色，如果这个图不是M可着色的，就回答‘no’，如果是M可着色的，则要找出所有不同的着色方法，目前我们认为，此方法是解决该问题的最佳选择。

 

解决问题之前先了解几个术语：

      局部有效着色：如果其中i个顶点已经着色，满足相邻两个顶点的颜色都不一样并且仍有颜色未被使用，就称当前的着色是局部有效着色。

无效着色：如果其中i个顶点已经着色，并且存在相邻两个顶点的颜色一样，就称当前的着色是无效着色。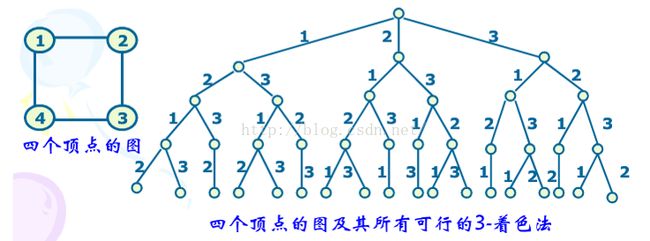

       我们假设一个实例来解决，如上图所示，平面图G=（V,E），V={V1,V2,V3,V4}，|E|=4;用M=3种颜色去着色，分别把这三种颜色的序号标为1、2、3。先把所有节点颜色设置零，从根节点开始，对根节点用第一种颜色进行着色，第一个肯定着色有效，接下去接着对下一个节点着色，先用第一种颜色对其节点着色，然后判断这个节点与相邻节点是否相同，有相同颜色则判定为无效着色，继续用第二种颜色着色，直到着色有效为止，如果与相邻节点颜色没有相同，则判定为有效着色，继续下一节点着色。

（2）、算法程序分析

bool ok()函数用于检查颜色的可用性，如果颜色在当前结点有效，则返回true，否则返回false。

Backtrack（）函数用于查找所有的可解方法。

GraphColor（）{                     //函数把所有查找到的结点进行着色，

for(i=1;i<=n;i++)                     //把所有结点的初始颜色设置为0

              color[i]=0;

while(color[k]<=m)

              {

                     cout<<"为第"<个节点上颜色"<

if(ok(k,c))                                  //有效则跳出循环

       {

              cout<<"着色有效"<

              break;

              }

       else                     //如果是无效着色，则另取一种颜色给当前节点

                     {

                            color[k]=color[k]+1;

                     }

 

color[k]<=m&&k==n         //若已经着色完全,则输出着色方案

color[k]<=m&&k

       k=k+1                          //着色未完全并且颜色够用，节点下移

}            

 

       k=k-1;                         //着色未完全并且颜色不够用，返回到父节点

 

       k<1;                                   //找不到着色方案

、程序流程图

、算法效率

图M着色问题用回溯法解决时，算法的时间上界可以通过计算解空间树种内结点的个数来估计，该问题中，解空间树中内结点数为 ,

对于每一个结点，在最坏情况下，ok检查当前结点的每一个儿子所相应的颜色的可用性需耗时O（m n）；因此该方法的时间复杂度为：  = nm(m^n-1)/(m-1)=O(nm^n);

（5）、结果与分析

按照上述例子，给定的无向图用m=3种颜色进行着色，用该例子检查算法的可用性。

       输入：顶点=4

                颜色=3

                无向图的矩阵：

                                                 0 1 0 1

                                                 1 0 1 0

                                                 0 1 0 1

                                                 1 0 1 0

输入方式及输出结果如下图所示：

                                                

该算法程序能较好的解决m图着色问题，但是如果算法输入较大的话，程序复杂度将大大增加，运行效率将会减小，该程序还需要很多优化的地方。

三、    结束语

回溯法是一种比较简单的算法。

 

 

参考文献：

[1]计算机算法设计与分析（第四版），王晓东，电子工业出版社，2012

[2]