机器翻译Transformer框架分析笔记 | Attention is all you need
个人笔记使用,可能记得比较乱,是针对大量文章总结而成,方便自己理解和复习
〇、笔记一中对Encoder-Decoder Attention理解有误
此注意力中的输入Q K V
其中K V应该是从编码器得到的输出乘以decoder子层随机初始化的W_K和W_V得到的
Q是上一步self-attention的输出乘以decoder子层随机初始化的W_Q得到的
注意:Decoder端中每个Decoder子层都有两组Q K V对应两组不同的W_Q,W_K,W_V
一、前期分析笔记
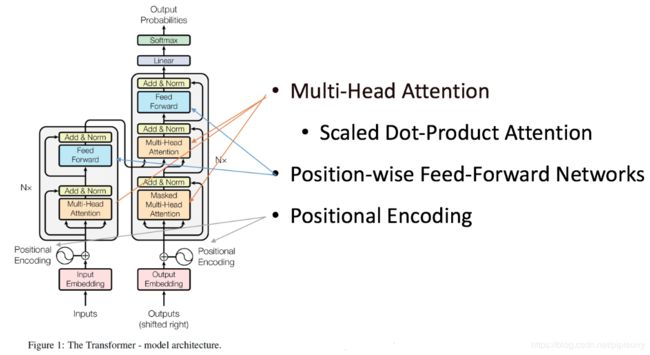
二、Transformer整体框架
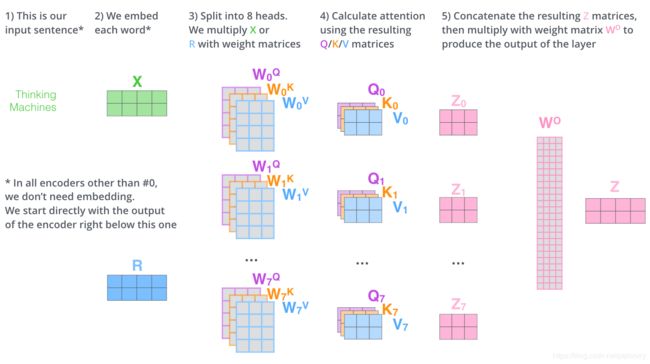
三、Transformer中的Self-attention
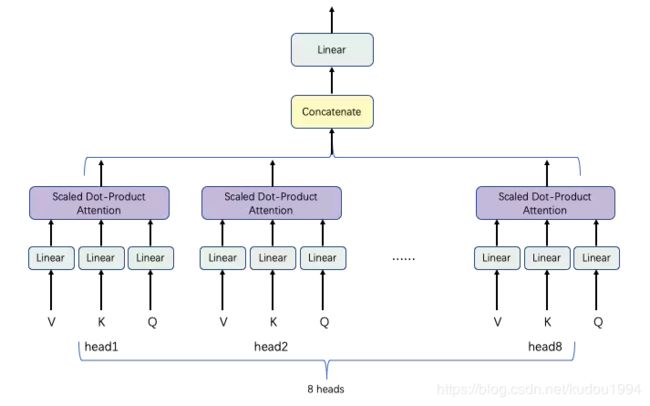
Multi-head attention与Scaled Dot-Product Attention
在Decoder端被称为Masked multi-head attention
Self-attention的字面理解:自注意力机制, Q K V都来自自身, 对输入本身做注意力。
在做自注意力处理之前,Q K V会先经过一个Linear层(乘以一个矩阵),线性变换,做维度变换:num_head * (d_q, d_k, d_v)
在做完点积注意力后,输出(多个z)要经过concat串联合并操作变成一个Z,因为Feed Forward一次只接收一个Z。
为什么会产生多个z呢?因为是多头注意力机制,一个头产生一个z,多个头就产生多个z。
多头怎样理解呢?其实就是人多好办事,每个人对同一个问题都有自己不同的看法,大致可能相同,但是具体肯定不同,所以就会有多个z。
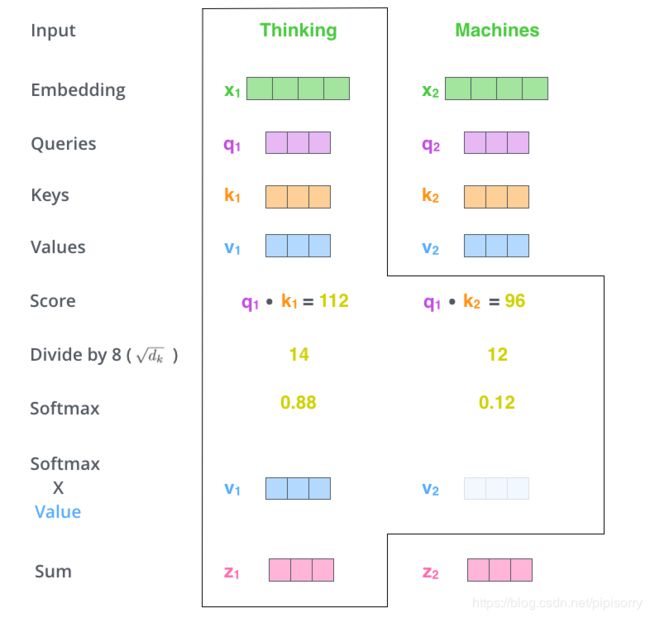
而在点积注意力中,Q K V作为输入,首先就要打分,打什么分呢?打的是我们一句话中所有的单词对我们的原始输入向量x1这个单词的关注度,所以让Q与K做点乘,得到一个分值例如96;
为了保持我们的梯度稳定,用得到的分值除以K向量维度的平方根,统一降低这个分值,得到12(起到调节作用,使得内积不至于太大,太大的话 softmax 后梯度很小,就非 0 即 1 了,不够“soft‘’,不利于反向传播的进行。);
这只是某个其他单词对我们输入的单词x1的关注度的打分,对于所有单词对x1的关注度打分我们做一个softmax归一化,使分值和为1全为正数(防止梯度爆炸)。对于得到的这些新的分值,乘以对应的V(每个词都有对应的Q K V)得到对应的加权向量z(增大对需要关注的词的关注度,减小无关词的关注度)。 将所有词关于单词x1的加权向量z相加,得到单词x1最终的self-attention的输出Z.
以上是一个单词在一头下的情况,实际使用时,输入应该是一句话,得到的输出也是一个矩阵,所以以上过程就要对应一个矩阵的输入输出形式。

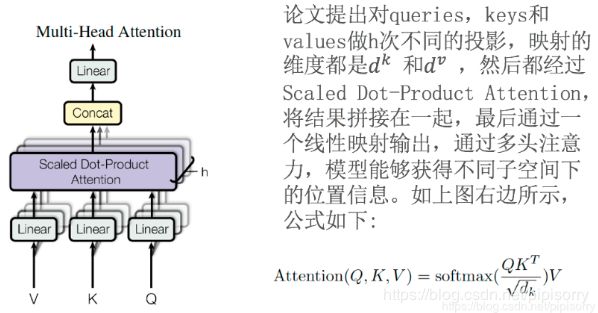
![]()
multi-head attention是通过h个不同的线性变换对Q,K,V进行投影,最后将不同的attention结果拼接起来(这跟 CNN 中的多个卷积核的思想是一致的)
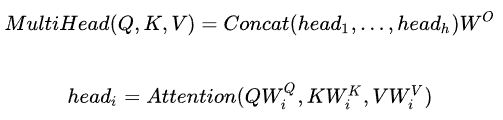
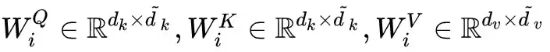
四、Q K V
这三个才是真正的输入,因为每一个Encoder子层或Decoder子层都有对应的输入和输出,所以他们的输入都是Q K V。
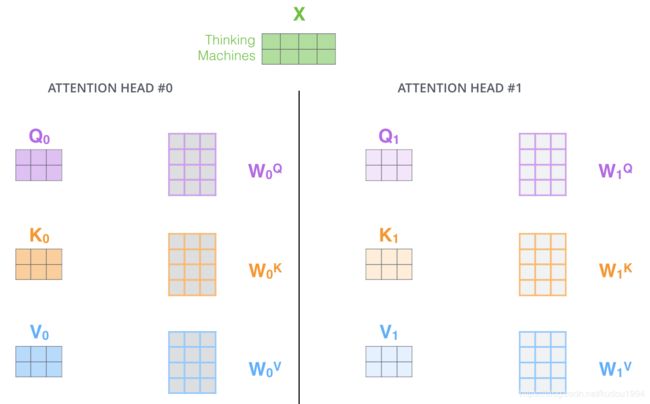
Q K V就是由一个向量(也许是最初的输入向量或者是上一步的输出向量)乘以对应的W转换矩阵得到的。
这个W转换矩阵是随机初始化而来,通过不断的训练而进行调整,一个子层中一头有一组Q K V。
而每一个Q K V都对应一个W矩阵,所以一个子层一头中有三个W矩阵,分别是W_Q, W_K, W_V
Note: 在一般的attention模型中,Q就是decoder的隐层,K就是encoder的隐层,V也是encoder的隐层。所谓的self-attention就是取Q,K,V相同,均为encoder或者decoder的input embedding and positional embedding,更具体为“网络输入是三个相同的向量q, k和v,是word embedding和position embedding相加得到的结果"。(原文这段话其实有点没看懂,QKV相等?????是想说‘Q K V所对应的原输入是同一个’这个意思吗?)
五、self-attention计算过程
六、实际应用中矩阵形式的计算
attention map
矩阵形式的Q*KT,得到一个word2word的attention map,再坐完softmax后横轴和为1
按行做归一化是因为attention的初衷是计算每个Query和所有的Keys之间的相关性
当句子很长时,attention map会非常大,会导致内存爆炸。解决方法:减小batch_size,采用多卡来弥补。或者直接减小句子长度。
在Decoder端中QKT得到一个attention map 但是我们要保证未来的词不影响当前词的预测,所以要对当前预测词之后的词使用mask的方式进行遮盖。一般的 Mask 是将填充部分置零,但 Attention 中的 Mask 是要在 softmax 之前,把填充部分减去一个大整数(这样 softmax 之后就非常接近 0 了)。

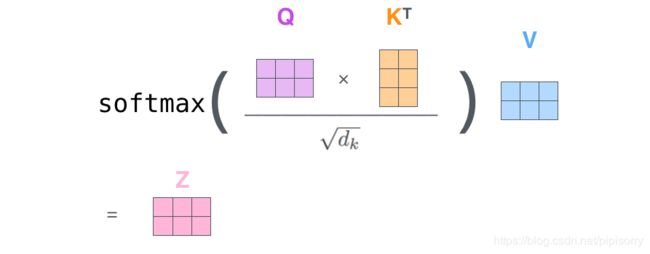
softmax后可以再加个dropout,然后再multiply V
合并后的Z,乘以一个随机初始化的W0得到输出Z
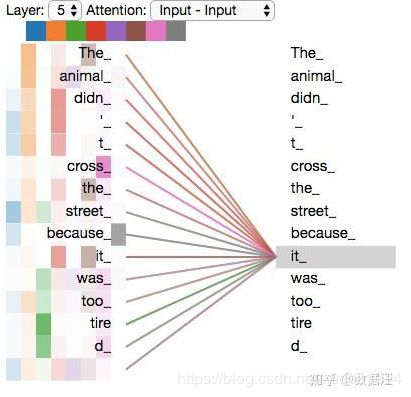
七、单词间的关注度
以下展示了输入的一句话中所有单词对单词it的关注度
图1是其中某一个头(颜色越深关注度越高)
图2是其中某两个头
图3是8个头
当头数大于1时,就很难直观的进行理解了。


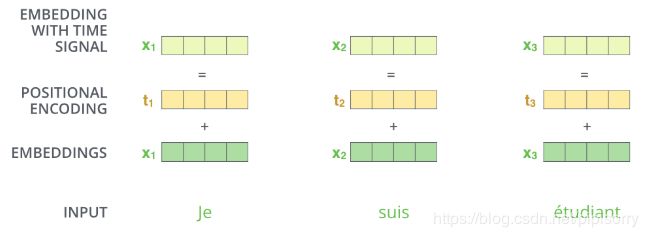
八、Transformer中的输入
输入包括Encoder端和Decoder端
输入由词向量和位置编码相加得到
九、Positional Embedding
由于Transformer是完全基于Attention的,在训练的过程中单词与单词之间的相对位置信息不能很好地被模型所捕捉到,所以为了让模型知道我们输入的句子中各单词的顺序/位置,并且在后续的训练之中模型可以学习到单词之间相对的特征,我们引入一个已经嵌入好的向量,加一个位置向量。(每个单词对应一个位置向量)
这个位置向量的每个值都在-1与1之间。
Positional Encodiung生成的方法:
1.用不同频率的sin和cos函数直接计算,生成固定的编码
2.训练出一份位置编码 参考论文
效果相差无几,所以采用第一种方法。
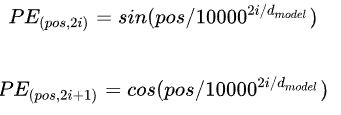
目的:
我们做位置编码的目的就是要捕捉各个单词的位置信息,告诉模型,这个it单词在原句总处在什么位置,同时还可以告诉模型,it这个单词与animal这个单词或者其他单词之间的相对位置关系。那么随便一种编码其实都能规定出一种固定单词对应关系,我们为什么还要费这么大劲来获取这么复杂的数值关系呢?
因为sin,cos函数可以表示成为某两个向量的线性关系,这样我们就能体现出不同单词之间的相对位置关系了。

摘自柚子皮大佬,这是我找到的关于位置编码解释的最好的一段话。
并且能提高准确率、减弱过拟合。

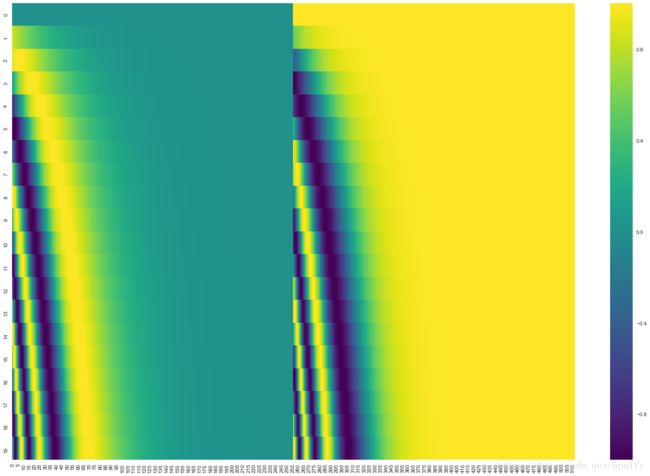
下图是某20个词的位置编码,每个单词共512维,前256维的值用sin函数获得,后面256维的值用cos函数获得。
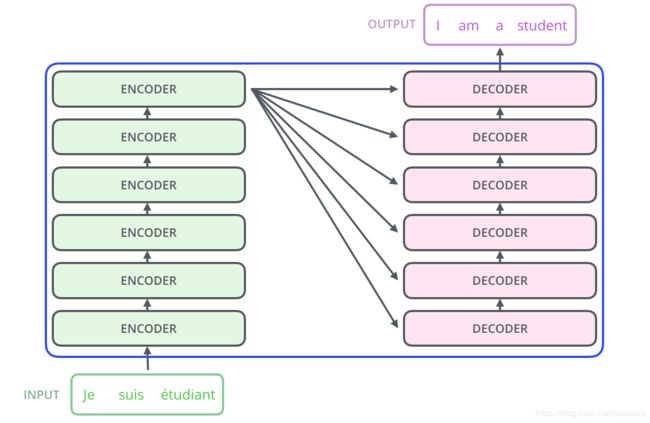
十、Encoder与Decoder
图中只显示了一个,实际当中有N个,也就是“多头”,但都共享一个输入
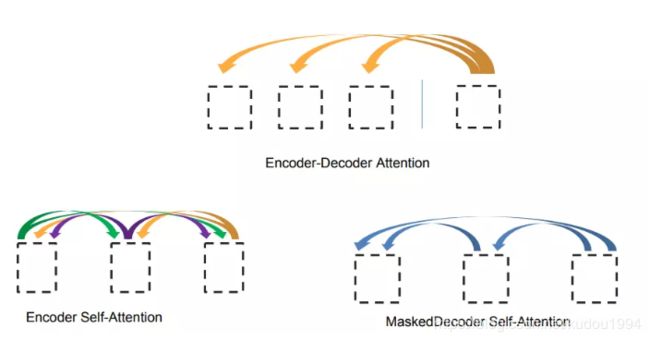
编码器最终的输出转化为K和V(K=V),传给解码器的每一个子层中的Encoder-Decoder Attention,作为Encoder-Decoder Attention的K和V。而Encoder-Decoder Attention之前一步的Masked Multi-head attention的输出转化为Encoder-Decoder Attention中的Q。
所以说Encoder-Decoder Attention不需要初始化Q K V 他的输入Q K V都是前一步的输出和编码端的输出给的。
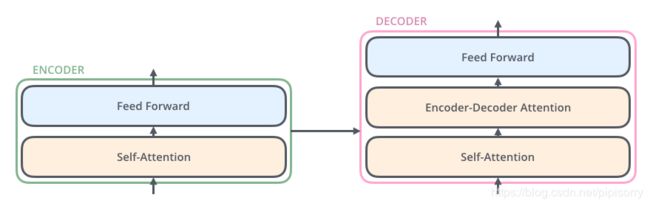
十一、Encoder子层与Decoder子层
Encoder-Decoder Attention
每一个子层之中都有一个自注意力和全连接前馈神经网络(有些文章中也称它为一种注意力机制)
Decoder端和Encoder大体相同,但是Decoder端中所有decoder子层中都多了一个Encoder-Decoder Attention
Transformer中的注意力机制都是多头的
十二、Add&Normalize
在每一个自注意力层之后都有一个Add&Normalize残差与归一化
残差结构的思想,来源于CNN
方便后面的数据处理,加快收敛,防止梯度消失

在一个Encoder子层中,首先由word voctor+Positional encoding生成输入向量z1,然后经过self-attention层输出得到z1,再由z1和原输入x1相加并归一化得到z1_new,z1_new作为此时的原输入经过Feed Forward再经过Add&Normalize得到最终Decoder#1层的输出,次输出作为Decoder#2的输入,直到Encoder端结束,得到最终的输出。
![]()
十三、Feed Forward 与 CNN
fully connected feed-forward network
Position-wise Feed-Forward Networks 事实上它就是窗口大小为 1 的一维卷积
位置全链接前馈网络——MLP变形,输入与输出维度相同
有两层dense,第一层的激活函数是ReLU(或者其更平滑的版本Gaussian Error Linear Unit-gelu),第二层是一个线性激活函数,整体来说就是做了一个非线性变换,如果multi-head输出表示为Z,则FFN可以表示为:
![]()
hidden_size变化为:512->2048->512,hidden_size维度 = dmodel维度
filter_size = dff = 内部层的维度 = 2048
十四、Decoder端的两种注意力
解码端和编码端大体相同,不同之处:
- 每一个Decoder子层都多了一个多头注意力Encoder-Decoder Attention,因此每一个Decoder子层有两组不同的Q K V与W_Q,W_K,W_V,不需要masking(因为在前一步已经masking过了,并且encoder的输出是可以看到所有词的)
- Decoder端中的self-attention是 masked multi-head attention(需要添加mask步骤) 在计算Q*KT得到的attention map后,要对当前预测词以后的词进行遮盖(接近0的数字)
- 上一次decoder的输出变成这次deocder的输入,Self-Attention 的Q K V来自上一次deocder的输出
- 在第一次进行解码时,没有真正的输入向量,输入向量是句子开始符 < start > 的向量。
- Self-Attention:当前翻译和已经翻译的前文之间的关系;Encoder-Decnoder Attention:当前翻译和编码的特征向量之间的关系。
十五、The Final Linear and Softmax Layer
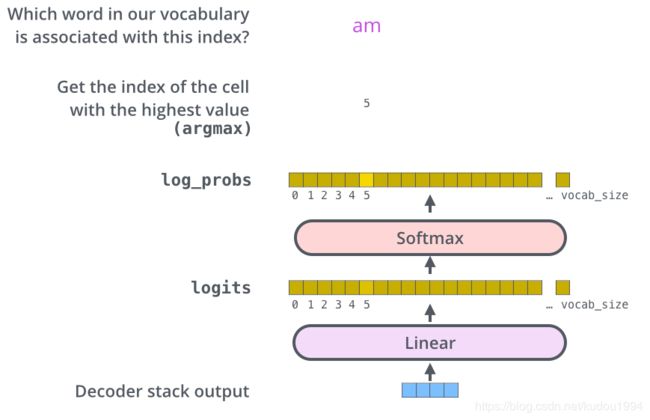
在N个Decoder子层输出之后得到的是浮点向量,需要这一步转化为我们真正的翻译
首先经过Linear全连接层,将decoder的输出映射到一个logits向量上(假设词表有10000个,那么这个logits向量就有10000维),这10000个元素对应的值表示词表中10000个词的可能倾向值,然后利用softmax转化为概率,这10000个概率中,哪个元素对应的概率最大,哪个元素对应原始词表中的那个词就是我们的翻译。
十六、流程动图
Decoder的结束:直到输出一个终止符。
这张图可真是太秀了,一下子就豁然开朗了
十七、Auto recursive decoding 自动递归解码
整个从Encoder到Decoder再到最终的结果整个过程,每一轮翻译出一个单词就要依靠这一轮Encoder的输出和上一轮Decoder的输出,这是一种递归过程。
越到后面Decoder需要的数据越多,计算量增加,但都属于递归方式。
十八、Training
训练过程,我们做一个德语到英语的翻译
假设我们有一个句子,让它走一次这个transformer流程,得到一个翻译后的英文句子。
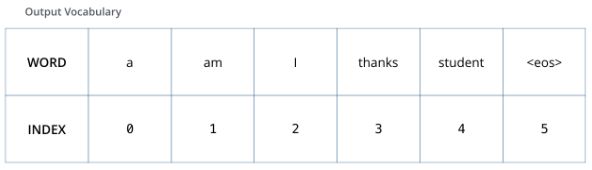
假设这是我们在训练之前就已经生成好的一个词汇表其中的英语部分的所有单词,“eos”(end of sentence的缩写形式)。
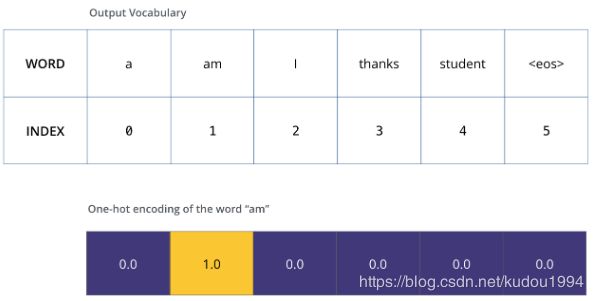
利用我们已有的词汇表,可以将am这个单词用one-hot编码进行表示,我们得到的这个one-hot编码的向量表示什么呢?表示的是标准翻译。我们将德语的一句话经过我们的模型输出一句英文句子,接着我们让模型得到的句子和我们标准翻译的句子的编码进行对比,然后用反向传播算法来略微调整所有模型的权重,生成更接近结果的输出。
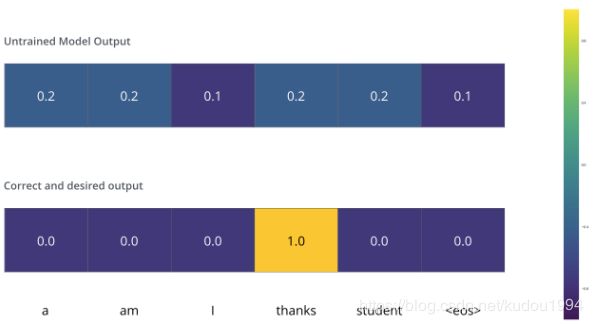
由于模型参数是随机初始化的,未训练的模型输出随机值。我们可以对比真实输出,然后利用误差后传调整模型权重,使得输出更接近与真实输出
The Loss Function
接着上面,那我们怎样进行比较呢?怎样比较两个概率分布呢?我们可以简单地用其中一个减去另一个。
还可使用交叉熵和KL散度。
上面的例子是对于单个单词而言,而在实际情况当中,我们是针对的一句话的输出对比,那么我们期望模型输出连续的概率分布满足如下条件:
- 每一个单词的概率分布向量维度与词汇表中词的个数相同
- position#1概率分布在与“i”关联的单元格有最高的概率
- position#2概率分布在与“am”关联的单元格有最高的概率
- 以此类推,第五个输出的分布表示“”关联的单元格有最高的概率
下面这张图表示的是标准翻译对应的概率分布(对应单词都为1,其余都为0)
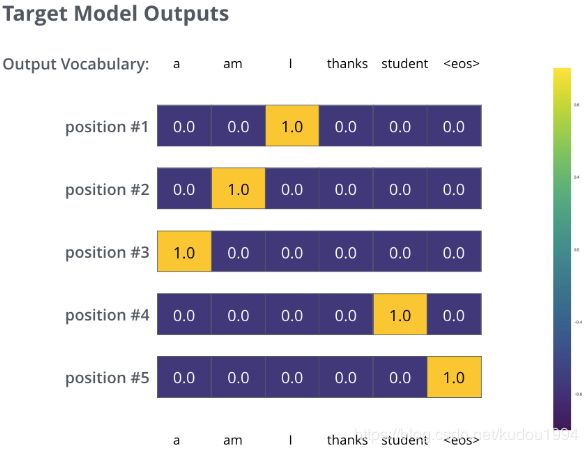
在一个足够大的数据集上充分训练后,我们希望模型输出的概率分布看起来像这个样子:
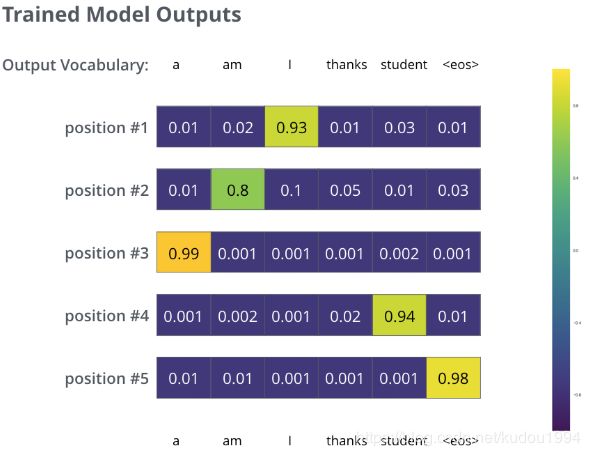
注意到每个位置(词)都得到了一点概率,即使它不太可能成为那个时间步的输出——这是softmax的一个很有用的性质,它可以帮助模型训练。
greedy decoding & beam search
因为这个模型一次只产生一个输出,不妨假设这个模型每次只选择概率最高的单词,并把剩下的词抛弃(比如说position#1,0。93是该行中概率的最大值,我们就认为position#1这一步输出的单词是:I),这是其中一种方法(叫greedy decoding贪心解码)。
另一个方法是留住概率最高的两个单词,这个时候上面那张图就不适用了,不过我们假设,第一次输出position#1得到的概率分布依次为:[0.3, 0.02, 0.6, 0.01, 0.05, 0.02],取概率最高的两个对应的单词为:I 和 a ,那么在预测position#2时跑两次模型:第一次假设 I 为上一轮的输出,第二次假设 a 为上一轮的输出。之后分别得到了position#2的概率分布,我们计算positions #1 和position #2的误差,哪个误差小我们就用哪个。然后就得到了position#1的预测值;不断的重复知道终止符的出现。这个方法被称作集束搜索(beam search)。
上面的例子中,beam_size = 2(因为我们在进行完position#1和position#2后就进行了误差分析,返回了正确的position#1的预测值),top_beams = 2 (每次取概率最高的2个值),这些都是可以调整的超参数。
上面这一段我感觉可能理解有点偏差,英语好的请自行阅读原文:
Now, because the model produces the outputs one at a time, we can assume that the model is selecting the word with the highest probability from that probability distribution and throwing away the rest. That’s one way to do it (called greedy decoding). Another way to do it would be to hold on to, say, the top two words (say, ‘I’ and ‘a’ for example), then in the next step, run the model twice: once assuming the first output position was the word ‘I’, and another time assuming the first output position was the word ‘me’, and whichever version produced less error considering both positions #1 and #2 is kept. We repeat this for positions #2 and #3…etc. This method is called “beam search”, where in our example, beam_size was two (because we compared the results after calculating the beams for positions #1 and #2), and top_beams is also two (since we kept two words). These are both hyperparameters that you can experiment with.
十九、论文其他内容
1. Optimizer:Adam
我们使用Adam优化器,其中β1 = 0.9, β2 = 0.98及ϵ= 10-9。 我们根据以下公式在训练过程中改变学习率:
![]()
这对应于在第一次训练到步骤为warmup_steps后线性地增加学习速率,然后与步骤数的平方分之一成比例地减少学习率。我们使用warmup_steps = 4000。
2. 正则化
Residual Dropout:
在Add&Normalized之前对每个attention和Feed Forward的输出都进行dropout,并且在Encoder端和Decoder端的输入中,在embeddings 与 positional encodings相加之后也进行dropout
Label Smoothing:
对输入做平滑处理,让编码中的0变成近似0,让1变成近似1.
这让模型不易理解,因为模型学得更加不确定,但提高了准确性和BLEU得分。
3. checkpoints average
通过对不同阶段生成的CKPT进行平均以得到更好的模型(一般不超过20个,实测16个效果不错?)
4. 长度惩罚α
在论文《Google’s Neural Machine Translation System: Bridging the Gap
between Human and Machine Translation》里:
在解码过程中,我们使用beam search来寻找序列y,该序列y在给定的训练模型下最大化得分函数s(Y, X)。我们介绍了基于最大概率的波束搜索算法的两个重要改进:覆盖惩罚和长度归一化。通过长度归一化,我们试图解释这样一个事实,即我们必须比较不同长度的假设。如果没有某种形式的长度归一化,规则的波束搜索将平均偏爱较短的结果而不是较长的结果,因为在每一步都添加了一个负对数概率,从而对于较长的句子产生较低(更多负)的分数。我们首先尝试简单地除以长度来归一化。然后,我们改进了原来的启发式算法,将其除以α,其中α是在一个开发集上优化的。最后,我们根据注意模块设计了一个经验上更好的评分函数,它还包括一个覆盖惩罚,以支持完全覆盖源句的翻译。
在谷歌的这篇论文中通过实验说明α在0.6-0.7的时候是最优值,其实不然,通过在做项目的时候大量的decoder证明,不一定。
二十、Transformer的优缺点
优点:
-
作者用最小的序列化运算来测量可以被并行化的计算。也就是说对于某个序列x1,x2,…,xn,self-attention可以直接计算xi,xj的点乘结果,而rnn就必须按照顺序从x1计算到xn
-
这里Path length指的是要计算一个序列长度为n的信息要经过的路径长度。cnn需要增加卷积层数来扩大视野,rnn需要从1到n逐个进行计算,而self-attention只需要一步矩阵计算就可以,Transformer 在结构上优越,任何两个 token 可以无视距离直接互通。所以也可以看出,self-attention可以比rnn更好地解决长时依赖问题。当然如果计算量太大,比如序列长度n>序列维度d这种情况,也可以用窗口限制self-attention的计算数量。
-
Attention 层的好处是能够一步到位捕捉到全局的联系,因为它直接把序列两两比较(代价是计算量变为 (n2),当然由于是纯矩阵运算,这个计算量相当也不是很严重);相比之下,RNN 需要一步步递推才能捕捉到,而 CNN 则需要通过层叠来扩大感受野,这是 Attention 层的明显优势。
-
另外,从作者在附录中给出的例子可以看出,self-attention模型更可解释,attention结果的分布表明了该模型学习到了一些语法和语义信息
-
LSTM、GRU 还是最近的 SRU都是递归式进行训练,顺序进行(顺序计算的过程中信息会丢失,尽管LSTM等门机制的结构一定程度上缓解了长期依赖的问题,但是对于特别长期的依赖现象,LSTM依旧无能为力),RNN 的明显缺点之一就是无法并行,因此速度较慢,这是递归的天然缺陷。并且RNN 无法很好地学习到全局的结构信息,因为它本质是一个马尔科夫决策过程,递归公式为y = f(y, x)。CNN 的方案也是可行的,窗口式遍历,不依赖前一步的输出,可并行,比如尺寸为 3 的卷积,公式为y = f(xt-1, xt, xt+1),而且通过层叠来增大感受野,容易捕捉到一些全局的结构信息。而transformer框架则直接可以捕获全局信息,可并行,公式为y = f(x, x, x),直接将 xt 与原来的每个词进行比较,最后算出 yt。
缺点:
- 实践上:有些rnn轻易可以解决的问题transformer没做到,比如复制string,尤其是碰到比训练时的sequence更长的时。
- 理论上:transformers非computationally universal(图灵完备),这种非RNN式的模型是非图灵完备的,无法单独完成NLP中推理、决策等计算问题(包括使用transformer的bert模型等等)。
- 粗暴的抛弃RNN和CNN虽然非常炫技,但是它也使模型丧失了捕捉局部特征的能力,RNN + CNN + Transformer的结合可能会带来更好的效果。
- 无法对位置信息进行很好地建模,这是硬伤。尽管可以引入 Position Embedding,但我认为这只是一个缓解方案,并没有根本解决问题。举个例子,用这种纯 Attention 机制训练一个文本分类模型或者是机器翻译模型,效果应该都还不错,但是用来训练一个序列标注模型(分词、实体识别等),效果就不怎么好了。那为什么在机器翻译任务上好?我觉得原因是机器翻译这个任务并不特别强调语序,因此 Position Embedding 所带来的位置信息已经足够了,此外翻译任务的评测指标 BLEU 也并不特别强调语序。(看过一篇文章有说,加和不加位置编码,在机器翻译之中效果相差不大)
廿一、参考文献
- The Illustrated Transformer(神文啊!图文并茂!)
- 一文读懂「Attention is All You Need」| 附代码实现
- Attention Is All You Need(论文网页版)
- Attention Is All You Need(论文PDF)
- 使用Excel和tensorflow实现Transformer(通过简单的例子走了一遍transformer流程)
- 神经机器翻译 之 谷歌 transformer 模型
- 深度学习:transformer模型——柚子皮
- BERT大火却不懂Transformer?读这一篇就够了
- transformer 各个部分主要内容——hpulfc
- 论文笔记:Attention is all you need
- Google’s Neural Machine Translation System: Bridging the Gap between Human and Machine Translation