动图详细讲解 LeNet-5 网络结构

LeNet-5 动图详细讲解网络结构

LeNet-5 是 Yann LeCun 等人在1998年设计的用于手写数字识别的卷积神经网络，当年美国大多数银行就是用它来识别支票上面的手写数字的，它是早期卷积神经网络中最有代表性的实验系统之一。本文将重点讲解LeNet-5的网络参数计算和实现细节。

1. LeNet-5全貌

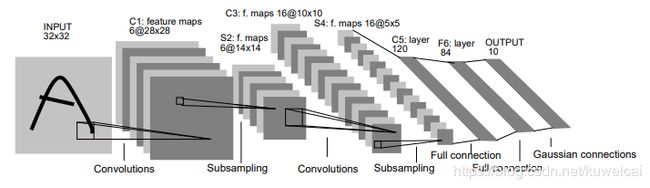
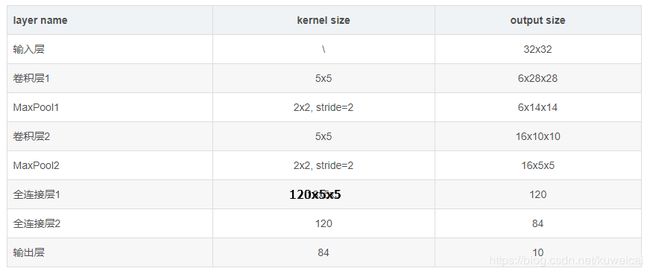
LeNet-5是一个7层卷积神经网络（一般输入层不计，也许有人会问，这个网络的名字里面为什么有个5, 其实这个网络的主干就是5层， 两个卷积层 + 两个全连接层 + 输出层）。上图已经清晰的标明了各层神经网络的参数了，整理如下。

这里推荐下面两个网站，可以动图的展示LeNet-5的计算过程。
2D效果 http://scs.ryerson.ca/~aharley/vis/conv/flat.html

3D效果 http://scs.ryerson.ca/~aharley/vis/conv/

2. 超参数与连接数

2.1 C1卷积层

如果对卷积过程还不是很清楚的朋友可以参考 卷积动图。

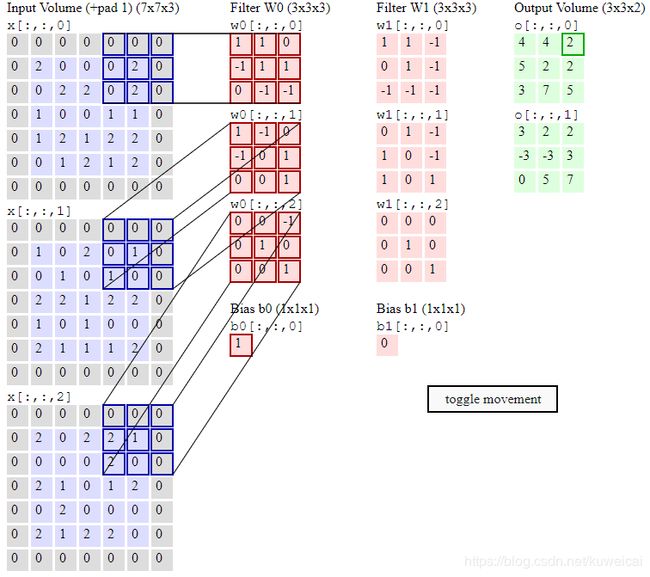
不同点在于上面的输入图像和kernel都是三通道的， 而我们这里都是单通道的。
这里kernel size 为 $5\ast 5$, 每一个 kernel 对应一个偏置项（bias），这样每一个 kernel 对应的超参数个数为 $5\ast 5+1=26$。总共有6个kernel。

• 超参数

$$(5\ast 5+1)\ast 6=156$$

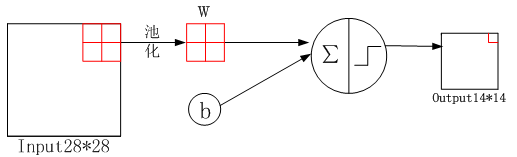
每一个卷积层的输出像素点对应 $5\ast 5+1=26$ 个连接（参考下图）。

• 连接数

$$(5\ast 5+1)\ast 28\ast 28\ast 6=122304$$

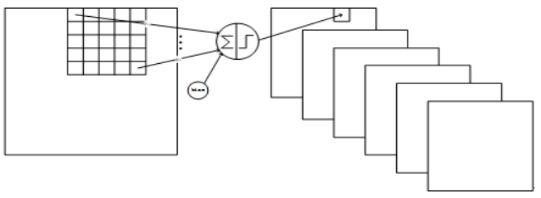
2.2 S2池化层

池化就是下采样（子抽样）过程，对图像进行子抽样，可以减少数据处理量同时保留有用信息。这里采用的是最大池化。

• 超参数

$$(1+1)\ast 6=12$$
其中第一个1为和的权重，池化可以看成输入图像与池化kernel（对应最大像素的位置的权重为1，其他位置均为0）的乘积， 如下所示。第二个1为偏置。

$$y=w\ast \left[\begin{array}{cc}1& 2\\ 3& 4\end{array}\right]\ast \left[\begin{array}{cc}0& 0\\ 0& 1\end{array}\right]+bias=4\ast w+bias$$

• 连接数

$$(2\ast 2+1)\ast 14\ast 14\ast 6=5880$$
虽然只选取 $2\ast 2$ 感受野中最大的那个数，但也存在 $2\ast 2$ 的连接数，即最大的权重为1，其余的为0。

2.3 C3卷积层

这里需要注意的是上面S2的输出为6个featuremap，但是经过本层之后输出变为16个featuremap。C3的前六个特征图(0,1,2,3,4,5)由S2的相邻三个特征图作为输入，接下来的6个特征图(6,7,8,9,10,11)由S2的相邻四个特征图作为输入，12,13,14号特征图由S2间断的四个特征图作为输入，15号特征图由S2全部(6个)特征图作为输入。
文字描述有点令人费解，直接查看上面的2D效果， 可以方便的查看每一个featuremap是如何产生的。

• 超参数

$$6\ast （3\ast 25+1）+6\ast （4\ast 25+1）+3\ast （4\ast 25+1）+（25\ast 6+1）=1516$$

• 连接数

$$10\ast 10\ast 1516=151600$$

2.4 S4池化层

这里和S2的计算类似。

• 超参数

$$(1+1)\ast 16=32$$

• 连接数

$$(2\ast 2+1)\ast 5\ast 5\ast 16=2000$$

2.5 C5卷积层（全连接）

这一个卷积层比较特殊，因为S4输出的featuremap的size为 $5\ast 5$, 正好和卷积的kernel size相等，因此卷积结果的size $1\ast 1$， 所以这里实质上是一个全连接层。因为 kernal size 的 channel 是120， 因此输出为 $120\ast 1\ast 1$。

• 超参数

$$(5\ast 5\ast 16+1)\ast 120=48120$$

• 连接数

$$（5\ast 5\ast 16+1）\ast 120\ast 1\ast 1=48120$$

2.6 F6全连接层

• 超参数

$$(120+1)\ast 84=10164$$

• 连接数

$$(120+1)\ast 84=10164$$

2.7 输出层（全连接）

• 超参数

$$84\ast 10=840$$

• 连接数

$$84\ast 10=840$$

3. 超参数的初始化

前面计算了超参数的个数，但是对于每一个超参数，又是如何初始化的呢？初始化的方式很多，这里仅仅以caffe中关于Lenet-5的示例程序为例用的就是 Xiaver 方式。如果想了解更多初始化方式请参考。

4. 小结

• LeNet-5 是一个7层卷积神经网络
• 总共有约6万（60790）个超参数
• 随着网络越来越深，图像的高度和宽度在缩小，与此同时，图像的 channel 数量一直在增加。