MATLAB 深度学习：自编码（含MATLAB）

本节将研究深度学习网络权值设计的重要思想之一：自编码思想，在正式介绍之前先以一个简单的介绍一篇，一层隐含层网络的自编码学习问题。

那么这种网络有什么实际应用呢？自动编码器（Autoencoder）是当前深度学习研究的热点之一，有很多重要的应用领域，这里仅举一个有趣的例子，大家还记得前一段时间百度推出的上传你的照片，系统帮你找到与你像的明星吗？其实这个功能就可以用自编码器（Autoencoder）来实现，首先，我们将已经训练好的自动编码器（Autoencoder）的输入层和中间层组成的网络拿出来，将所有明星的脸进行压缩，得到一个人脸向量，保存起来，然后，当普通用户上传了自己的照片后，系统将用户照片输入自动编码器（Autoencoder）的输入层，从中间层得到该用户的人脸向量，最后拿这个用户的人脸向量与明星们的人脸向量进行比较，找出向量距离最近的一个或几个明星，将明星的照片作为与用户最像的明星照片，返回给用户。由于百度这项服务推出的时间较早，应该不是基于自动编码器实现的，但是使用自动编码器，完全可以实现这个功能，有兴趣的读者完全可以试一下。

当然去噪自动编码机（Denosing Autoencoder）更大的应用是作为深度学习中的一层，堆叠在一起形成深度学习网络。

自编码是一种非常简单的BP神经网络，是一种无监督学习算法。

在一般BP神经网络中，进行数据训练时，对一组输入数据，就会对应一组输出数据，通过调整预测输出数据跟真事输出数据的差值（表示成代价函数的形式），对权值进行微调，从而得到各层网络的权值。但是对于某些输入来说，其输出 是得不到的，那么如何训练这些数据，得出这些数据的特性？就是通过使输入等于输出。

以一个简单三层网络为例如下：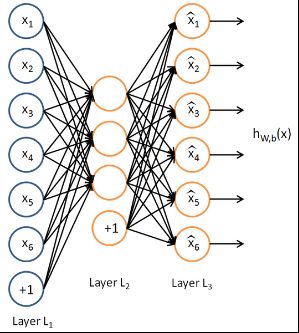 
 
这里我们假设输出等于输入来训练这个网络参数（可能训练好的网络参数不可能让输出百分百等于输入，至少会非常接近吧）。那么这个网络在输入确定了以后（这时输出也就确定了吧），唯一需要确定的就是隐含层的个数了吧，以上述这个图为例，我们可以看到，网络的输入与输出都是一个6维的向量，而隐含层是3个，也就是3维。

那么这种自编码有什么意义呢？它又有什么用呢？可以看到，自编码可以使得网络通过学习转化成一组另外的量，这组量又可以通过译码恢复成原始的量，这个过程就相当于先求函数，再求反函数的过程，如果通过网络求得的函数（也就是图中输入和隐层之间的对应关系）其对应的反函数能够最大限度的反应出最原始的输入，说明这个函数能够真实体现出输入数据的特性，是原始数据的另外一种表达形式。也就是说，原始的量可以通过编码映射成另一组量吧，这一组量既然可以通过译码恢复成原始的量，说明了什么？中间这一层的输出是不是就是原始输入的另外一种表达了？是的。这就好比一个人，你看得到时候直接看就是一个人，当你看不到人的时候，比如说你听到了他的名字，你也知道这个名字表示的就是这个人。所以这个名字就是这个人的另一种条件下的新特征，而往往这种新特征更能去分这个人是谁。

1. 好了再看看上面这个图，输入6维，隐含层以后变成了3维，输出还是6维，我们单看到隐含层发现了什么？是不是输入从6维降到了3维？但是这3为在某种意义上还是原始数据的典型特征吧，言外之意是不是相当于降维了。如果知道主成分分析法（PCA）的人应该了解，pca方法其实就是实现数据降维的，那么在这里我们通过这种自编码，规定隐含层神经元的个数以后，通过自编码的训练，让网络的输出尽可能的等于输入，待自编码完成后（也就是误差达到可接受范围），那么输入通过隐含层的输出就相当于降维了吧（前提是隐含层的神经元个数要小于输入维数，这样才叫降维，否则的话叫升维），说到升维，了解PCA的朋友你们有没有试过PCA升维呢？PCA能不能升维呢？哈哈，貌似不能，没试过。但是理论上是可以的。那么升维相当于将信息复杂化，这种操作有没有用呢？可能还是有用的吧，了解SVM的朋友知道，SVM里面就有将非线性数据通过升维以后可以在线性范围内可分，那么这里的升维是不是也能将原始非线性的数据变到线性呢？可以去试试看，应该有那么个意思。则这个问题就变成了一个线性代数中的主成份分析问题了。假设中间层有k个节点，就变成由输入信号x的前k个主成份项，来近似表示原始输入信号。关于这个问题，我们会在深度学习数学基础的线性代数章节中，详细分析这一过程。

因为y可以视为x的有损压缩形式，通过我们的优化算法，可以对训练样本产生很好的压缩效果，同时在测试样本集上有很好的表现，但是我们并不能保证网络可以所有样本都有好的压缩效果。
随着对自动编码器的研究，研究者们发现，对于采用非线性编码器，随机梯度下降算法时，当中间层神经元个数大于输入层神经元个数时，网络误差和泛化的效果会更好一些。
这是什么原因呢？因为我们采用的是随机梯度下降加早期终止优化算法，我们的自动编码器编码层非线性神经元的连接权值需要非常小，才能模拟出线性变换的效果，同时，对于解码网络，又需要非常大的权值，才能有效的恢复原始信号（可以想像成编码层是乘以一个数，而解码层是乘以这个数的倒数），而我们的优化算法，很难产生特别大的连接权值。因此，我们的自动编码器只能拟合于我们的训练样本集。增加中间层神经元的数量，可以在一定程度上解决这个问题。
但是，如果我们把自动编码器的编码层视为对输入信号的压缩，如果中间层的神经元数量多于输入层，那么不仅没有实现压缩，反而使信号扩大了。这就未免太搞笑了。为此，很多研究人员提出，可以通过向中间层神经元引入稀疏性，使大部分神经元为0或者接近为0，从而达到信号压缩的目的。从实践上来看，这种方法的效果还不错。这种方法为去噪自编码。

我们在这里介绍的是另一种方法，来解决自动编码器编解码性能问题。与上面增加中间层神经元数量的方法不同，在这里我们通过向编解码过程中添加随机噪音来解决这一问题，这也是我们为什么把今天所介绍的网络称为去噪自动编码机（dA）的原因。

这个方法的核心思想很简单，就是随机的将原始信号的一些维度数值变为0，有时甚至可以达到一半左右，将这个加入了随机噪音的信号输入我们的去噪自动编码器，将得到的输出与原始输入信号之间计算误差，还是采用前面的随机梯度下降算法，对权值进行调整，使误差达到最小。如果网络可以做到这一点，就可以视为网络自动将我们人为加入了随机噪音去掉了。
我们自然会问，为什么要这样做呢？实际上，对于如图像信号而言，很多信号内容是冗余的，去掉之后不影响信息量，例如当图像信号有一些雪花时，我们还是可以识别出图像内容的。这说明让自动编解码机去噪是可能的。至于加入噪音的原因，是因为我们人对图像内容的理解，完全可以在某些信息缺失的情况下得出结论，如图像中物体被遮盖、破损的情况下，我们依然可以识别图像中的物体。去噪自动编码机（dA）通过加入随机噪声，试图使神经网络也具有与人类似的能力

好了说了这么多，我们还是来看降维的情况，通过自编码实现数据的降维思想最初是2006年深度学习领域大牛Hinton想出来的，并且发表在顶级期刊Science上，文章的出处在这里：

“reducing the dimensionality of data with neural networks”

该篇经典之作也被视为深度学习的开山之作，自此以后深度学习火了起来，并且逐渐打败传统模式识别领域的浅层学习算法。我们知道，机器学习或者模式识别，对数据的主要工作在做什么？无非提取数据的主要特征，那么以前可能所有的特征要么是人为设计出来，要么是浅层学习出来的，像PCA，他们虽然一定程度上有用，但是相对于深度学习这种将数据的各个层次的特征都学习出来了的相比自然弱了不少，这也是深度学习的最强大之处。

了解了自编码，下面我们来实际看看这种自编码的效果。 
这里以matlab平台实验，假设我们选取一系列小块图像（至于小块选多大，这里考虑速度原因，单台笔记本的计算原因，选择6*6的小块图像，其实这是很小了，所以效果不是很明显，大概这个意思）作为输出来进行三层网络的自编码学习，然后看看隐含层学习到的特征是什么。选择matlab是因为它自带神经网络的构造函数便于实验，关于其神经网络工具箱的使用介绍，看这篇

机器学习之实战matlab神经网络工具箱

好了开始实验吧，首先我们需要找到自编码的输入样本，这里我们以每个6*6的小块图像作为一个样本，先准备好很多这样的小块图像，假设准备1000个吧，至于怎么准备，你可以让每个小块假设是从某个大图像上随机截取的好了。

clc
clear
%选择块图像的大小
patch = [6,6];
%选择块图像的个数
num_pic = 1000;
data = zeros(num_pic,patch(1)*patch(2));
for i = 1:20
    pic_name = [num2str(i),'.jpg'];
    I = imread(pic_name);
    I = rgb2gray(I);
    for j = 1:50
        %随机选择块的位置
        choose_row = round((size(I,1) - 50)*rand);
        choose_col = round((size(I,2) - 50)*rand);
        %提取块并存起来
        I_patch = I(choose_row+1:(choose_row+6),choose_col+1:(choose_col+6));
        data((i-1)*50+j,:) = I_patch(:);
    end
end
%归一化到0-1
data = mapminmax(data, 0, 1);
save data.mat data        

• 1
• 2
• 3
• 4
• 5
• 6
• 7
• 8
• 9
• 10
• 11
• 12
• 13
• 14
• 15
• 16
• 17
• 18
• 19
• 20
• 21
• 22
• 23
• 24

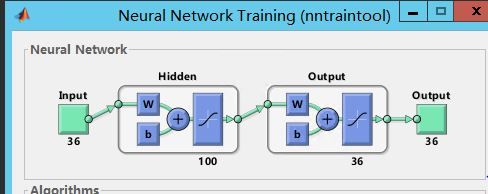
然后把这些样本既当成输入，也当成输出输送到神经网络中，比如这里我们就得到了1000*36的样本，每一行一个6*6的块，1000个这样的块，输出也是1000*36，就这样。接着就可以训练了，这里我们再取100个隐含层。那么假设训练好了。我们怎么可视化这个结果呢？因为我们需要看的是它自编码的编码部分，而不是译码部分，所以我们只关心编码部分的权值，像下面这个： 

比如x1经过隐含层的映射会有三个输出，那么这三个输出就是编码结果，同理其他的。而我们是需要把这个映射结果显示出来，也就是把x1映射的三个值显示出来，同理其他的。因为这里只有三个值，根本没办法可视化。所以像上面我们取了100个隐含层，把每个输入每个单元映射100个输出，再把100变成10*10图像，我们就可以显示了，并且这里我们也只是显示这些权值，把输出默认为全1看看。

好了，那么采用matlab工具箱，上述data选择完后，构造神经网络模型，简单的几行代码：

clc
clear
load data
% data = data(1:100,:);
%% 神经网络的构建与训练
% 构造神经网络(包含100个隐藏层的节点)
net = feedforwardnet(100);
net.layers{2}.transferFcn = 'tansig';% 输出的映射方法，默认purelin--线性映射
% 训练网络
net = train(net,data',data');
% 可视化权值
show_result(net);

• 1
• 2
• 3
• 4
• 5
• 6
• 7
• 8
• 9
• 10
• 11
• 12
• 13

这样matlab自带它的训练模型就出来了： 

可视化的函数也很简单：

function show_result(net)
% 将输入到隐含层的权值提出来并显示
W1 = net.IW{1};
[~,n] = size(W1);
for i = 1:n
    im = W1(:,i);
    im = reshape(im,10,10);
    subplot(6,6,i);
    imshow(im,[]);
end

• 1
• 2
• 3
• 4
• 5
• 6
• 7
• 8
• 9
• 10
• 11

最终得到结果如下： 

可以看到输出的编码样子，有点像却很不明显，原因就是这是由36到100的升维，大了电脑带不动，在matlab的这个自带工具箱下。

所以，即使我们选择的块只有6*6，1000个块，然而这个训练过程却很漫长，为什么？就是matlab自带的神经网络并不是适合这种自编码的训练，而是浅层的输入到输出的训练，真正的自编码训练需要特定的设计才能保证速度，这里只是强制使用着看看，同时自编码还可以优化，比如加入稀疏变成稀疏自编码等等，后面介绍一种工具箱来重新实验这种自编码。