ML模型1:线性回归
线性回归
- 1. 线性模型表示
- 2. 最小二乘法
- 3. 最大似然估计
- 3.1 误差
- 3.1 最大似然估计
- 4. 求解
- 4.1 求解-正规方程法:
- 4.2 求解-梯度下降
- 5. 评估方法
- 6. 广义线性模型
- 7. Sklearn 示例
- Q&A
回归在数学上来说是给定一个点集,就能够用一条曲线去拟合之。如果这个曲线是一条直线(超平面),那就被称为线性回归。若不是一条直线则称为非线性回归,常见有多项式回归、逻辑回归等。
线性模型优劣:
优点:结果易于理解,计算上不复杂;
缺点:对非线性的数据拟合不好
1. 线性模型表示
一般线性模型表示:
y ^ = θ 0 + θ 1 x 1 + θ 2 x 2 + ⋯ + θ n x n \hat{y} = \theta_0 + \theta_1x_1 + \theta_2x_2 + \cdots + \theta_nx_n y^=θ0+θ1x1+θ2x2+⋯+θnxn
其中 x 1 , x 2 x_1,x_2 x1,x2 等表示不同的特征,
θ 1 , θ 1 \theta_1,\theta_1 θ1,θ1 等表示特征权重
向量形式写成:
y ^ = h θ ( x ) = θ T x \hat{y} = h_\theta(x) = \theta^Tx y^=hθ(x)=θTx
2. 最小二乘法
线性模型用一个直线(平面)拟合数据点,找出一个最好的直线(平面)即要求每个真实点距离平面的距离最近。即使得残差平方和(Residual Sum of Squares, RSS)最小:
R S S ( X , h θ ) = ∑ i = 1 m ( θ T x ( i ) − y ( i ) ) 2 RSS(X, h_\theta) = \sum_{i=1}^m{(\theta^Tx^{(i)}-y^{(i)})^2} RSS(X,hθ)=i=1∑m(θTx(i)−y(i))2
另一种情况下,为消除样本量的差异,也会用最小化均方误差(MSE)拟合(Q1.为什么使用均方误差):
M S E ( X , h θ ) = 1 m ∑ i = 1 m ( θ T x ( i ) − y ( i ) ) 2 MSE(X, h_\theta) = \frac{1}{m}\sum_{i=1}^m{(\theta^Tx^{(i)}-y^{(i)})^2} MSE(X,hθ)=m1i=1∑m(θTx(i)−y(i))2
3. 最大似然估计
3.1 误差
使用最大似然估计前,先引入误差的概念。
真实值与误差值之间会肯定会存在差异(用 ε \varepsilon ε 表示误差),
且误差 ε ( i ) \varepsilon^{(i)} ε(i) 是独立并且同分布的,并且服从均值为 0 方差 σ 2 \bf{\sigma^2} σ2 的高斯分布
故对每个真实样本,有
y ( i ) = θ T x ( i ) + ε ( i ) {y^{(i)} = \theta^Tx^{(i)} + \varepsilon^{(i)}} y(i)=θTx(i)+ε(i)
3.1 最大似然估计
最大似然估计(maximum likelihood estimation, MLE)一种重要而普遍的求估计量的方法。通过调整估计参数,使得已经实现的样本发生概率最大。
由于误差服从高斯分布,先不考虑方差,则出现误差 ε ( i ) \varepsilon^{(i)} ε(i) 的概率为:
p ( ε ( i ) ) = 1 2 π σ exp ( − ( ε ( i ) ) 2 2 σ 2 ) p(\varepsilon^{(i)}) = \frac{1}{\sqrt{2\pi}\sigma}\exp(-\frac{(\varepsilon^{(i)})^2}{2\sigma^2}) p(ε(i))=2πσ1exp(−2σ2(ε(i))2)
将误差代入以上公式,得:
p ( y ( i ) ∣ x ( i ) ; θ ) = 1 2 π σ exp ( − ( y ( i ) − θ T x ( i ) ) 2 2 σ 2 ) p(y^{(i)}|x^{(i)};\theta) = \frac{1}{\sqrt{2\pi}\sigma}\exp(-\frac{(y^{(i)} - \theta^Tx^{(i)})^2}{2\sigma^2}) p(y(i)∣x(i);θ)=2πσ1exp(−2σ2(y(i)−θTx(i))2)
对已发生的样本,出现的概率为:
L ( θ ) = ∏ i = 1 m p ( y ( i ) ∣ x ( i ) ; θ ) = ∏ i = 1 m 1 2 π σ exp ( − ( y ( i ) − θ T x ( i ) ) 2 2 σ 2 ) L(\theta) =\prod_{i=1}^{m} p(y^{(i)}|x^{(i)};\theta) =\prod_{i=1}^{m}\frac{1}{\sqrt{2\pi}\sigma}\exp(-\frac{(y^{(i)} - \theta^Tx^{(i)})^2}{2\sigma^2}) L(θ)=i=1∏mp(y(i)∣x(i);θ)=i=1∏m2πσ1exp(−2σ2(y(i)−θTx(i))2)
两边去取对数:
l o g L ( θ ) = l o g ∏ i = 1 m 1 2 π σ exp ( − ( y ( i ) − θ T x ( i ) ) 2 2 σ 2 ) = ∑ i = 1 m l o g 1 2 π σ − 1 σ 2 ⋅ 1 2 ∑ i = 1 m ( y ( i ) − θ T x ( i ) ) 2 \begin{aligned} log\ L(\theta) &=log\ \prod_{i=1}^{m}\frac{1}{\sqrt{2\pi}\sigma}\exp(-\frac{(y^{(i)} - \theta^Tx^{(i)})^2}{2\sigma^2})\\ &=\sum_{i=1}^{m}log\ \frac{1}{\sqrt{2\pi}\sigma}-\frac{1}{\sigma^2}\cdot\frac{1}{2}\sum_{i=1}^{m}(y^{(i)} - \theta^Tx^{(i)})^2 \end{aligned} log L(θ)=log i=1∏m2πσ1exp(−2σ2(y(i)−θTx(i))2)=i=1∑mlog 2πσ1−σ21⋅21i=1∑m(y(i)−θTx(i))2
使出现概率最大,即使上面方程达到最大,通过简单变换转换成求最小值问题,得使以下方程最小:
J ( θ ) = 1 2 ∑ i = 1 m ( y ( i ) − θ T x ( i ) ) 2 J(\theta) =\frac{1}{2}\sum_{i=1}^{m}(y^{(i)} - \theta^Tx^{(i)})^2 J(θ)=21i=1∑m(y(i)−θTx(i))2
以上方程与最小二乘法相似,以下均以此函数作为损失函数。
4. 求解
主要求解方法有两种,正规方程法以及梯度下降法。有时候,写成矩阵写法会方便我们计算。
损失函数:
J ( θ ) = 1 2 ∑ i = 1 m ( y ( i ) − θ T x ( i ) ) 2 = 1 2 ( X θ − Y ) T ( X θ − Y ) J(\theta) =\frac{1}{2}\sum_{i=1}^{m}(y^{(i)} - \theta^Tx^{(i)})^2 =\frac{1}{2}(X\theta-Y)^T(X\theta-Y) J(θ)=21i=1∑m(y(i)−θTx(i))2=21(Xθ−Y)T(Xθ−Y)
4.1 求解-正规方程法:
J ( θ ) J(\theta) J(θ)可以通过直接求出最小值点,在最小值点, J ( θ ) J(\theta) J(θ)在各方向的偏导均为零。

附: 向量矩阵求导公式
分析
求逆操作 - 求逆十分耗时(假设 X T X {{\bf{X}}^T}{\bf{X}} XTX 尺寸n x n,特征数n超过1w时建议用迭代法),此外 X T X {{\bf{X}}^T}{\bf{X}} XTX X的逆矩阵可能不存在
应用场景 - 拟合函数是线性时才可以用
4.2 求解-梯度下降
梯度下降法基于的思想为:要找到某函数的极小值,则沿着该函数的梯度方向寻找。若函数为凸函数且约束为凸集,则找到的极小值点则为最小值点。
梯度下降基本算法为:
首先用随机值填充θ(这被称为随机初始化),然后逐渐改进,每次步进一步(步长α),每一步都试图降低代价函数,直到算法收敛到最小。
θ : = θ − α ⋅ ∇ θ J ( θ ) \theta:=\theta-\alpha\cdot\nabla_\theta J(\theta) θ:=θ−α⋅∇θJ(θ)
求解梯度常见有以下几个方法:
- 批量梯度下降(BGD)
批量梯度下降法为最小化所有训练样本的损失函数(对全部训练数据求得误差后再对参数进行更新),使得最终求解的是全局的最优解,即求解的参数是使得风险函数最小。批梯度下降一次迭代会更新所有θ,每次更新都是向着最陡的方向前进。

优点:得到全局最优解;易于并行实现;
缺点:当样本数目很多时,训练过程会很慢。
- 随机梯度下降(SGD)
随机梯度下降法为最小化每条样本的损失函数,虽然不是每次迭代得到的损失函数都向着全局最优方向, 但是大的整体的方向是向全局最优解的,最终的结果往往是在全局最优解附近。
也就是说我用样本中的一个例子来近似我所有的样本,来调整θ,其不会计算斜率最大的方向,而是每次只选择一个维度踏出一步;下降一次迭代只更新某个θ,抱着并不严谨的走走看的态度前进。

优点:训练速度快;
缺点:准确度下降,并不是全局最优;不易于并行实现。
- 小批量梯度下降(MBGD)
MBGD是一种介于SGD和BGD两种方法之间的一种折中的梯度下降法:在每一步中,不是基于完整训练集(如BGD)或仅基于一个实例(如SGD中那样)计算梯度,而是在小随机实例集上的梯度。
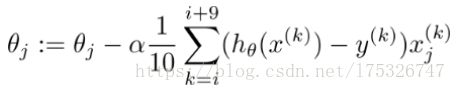
如下图所示,显示了训练期间三个梯度下降算法在参数空间中所采用的路径。 他们都接近最优值,BGD的路径最终停在最优值,而SGD和MBGD继续四处走动。 但是,不要忘记BGD需要花费很多时间来完成每个步骤,如果您使用了一个良好的学习计划表,Stochastic GD和Mini-batch GD也会达到最小。
分析
梯度下降法VS最小二乘法:
- 梯度下降法是迭代求解,最小二乘法是计算解析解
- 梯度下降法需要选择步长和初始值,最小二乘法不需要
- 样本量小且存在解析解,选择最小二乘法
梯度下降法VS牛顿法:
- 两者都是迭代法
- 梯度下降法等效一阶泰勒展开,牛顿法等效二阶泰勒展开(Q2.为什么梯度反方向是函数值局部下降最快的方向?)
- 牛顿法收敛更快(Q2.为什么)
5. 评估方法
模型建立后,一般使用 R 2 R^2 R2 评估拟合程度。
R 2 = 1 − ∑ i = 1 m ( y ^ i − y i ) 2 ∑ i = 1 m ( y i − y ˉ i ) 2 R^2 =1-\frac{\sum_{i=1}^{m} (\hat{y}_i-y_i)^2}{\sum_{i=1}^{m} (y_i-\bar{y}_i)^2} R2=1−∑i=1m(yi−yˉi)2∑i=1m(y^i−yi)2
6. 广义线性模型
如果数据实际上比简单的直线更复杂,我们仍然可以使用线性模型来拟合非线性数据。其本质为将特征(或y值)进行转换(取多项式、对数等)为新的特征(或y值),再将新的特征(或y值)加入到线性模型中。 若进行转换的是Y,则最终输出模型时需要进行逆变换。
若执行高维多项式回归,维度太高时可能会出现过拟合的情况,此时需要通过交叉检验选择适合的维度,同时也可以加入正则化项减少过拟合情况发生。这些以后再说。
7. Sklearn 示例
官方文档
from sklearn.linear_model import LinearRegression
model = LinearRegression() # 建立模型
参数
| 超参 | 解释 | 类型(默认值) |
| fit_intercept | 是否计算模型的截距;如果设置为 False,计算将不使用截距(即:期望数据已经进行了中心化处理) | boolean(True) |
| normalize | 是否将数据归一化;fit_intercept 设置为 False 时,这个参数可以忽略。如果设置为 True,回归之前将通过减去均值并除l2范数进行归一化。如果需要进行标准化,请在调用估计器 normalize=False的 fit 函数之前使用sklearn.preprocessing.StandardScaler | boolean(False) |
| n_jobs | 确定cpu的核数 (None表示1,-1 表示使用所有) | int or None(None) |
属性
| 属性 | 解释 | 类型 |
| coef_ | 回归系数(斜率) | array |
| intercept_ | 截距 | array |
Q&A
Q1. 为什么选均方误差?
- 为了回归分析,通常需要对随机误差项的概率分布做一些假设。误差服从高斯分布[PDF的指数项上包含差值平方],不考虑方差,然后利用最大似然估计,可以推出损失函数的表达式。(可以了解下高斯-马尔可夫定理)
- 最小二乘法的思想 - 选择未知参数,使得理论值与观测值之差的平方和达到最小(二乘就是平方的意思)
Q2.为什么梯度反方向是函数值局部下降最快的方向?
对函数 f f f 及任意一个单位向量 u u u, f f f 在 u u u 方向的变化率为 ∇ f T u = ∣ ∣ ∇ f ∣ ∣ 2 c o s ( θ ) ∇f^Tu = ||∇f||_2 cos(θ) ∇fTu=∣∣∇f∣∣2cos(θ) ,其中 θ θ θ 为向量 u u u和梯度 ∇ f ∇f ∇f 之间的夹角。因为 c o s θ ∈ [ − 1 , 1 ] cosθ ∈ [-1, 1] cosθ∈[−1,1],当 c o s θ = − 1 cosθ = -1 cosθ=−1,即 u u u和梯度 ∇ f ∇f ∇f 反方向时,变化率最小
Q3. 为什么牛顿法收敛更快?
通俗解释- 比如你想找一条最短的路径走到一个盆地的最底部,梯度下降法每次只从你当前所处位置选一个坡度最大的方向走一步,牛顿法在选择方向时,不仅会考虑坡度是否够大,还会考虑你走了一步之后,坡度是否会变得更大。所以,可以说牛顿法比梯度下降法看得更远一点,能更快地走到最底部。
Wiki解释- 几何上来说,牛顿法就是用一个二次曲面去拟合你当前所处位置的局部曲面,而梯度下降法是用一个平面去拟合当前的局部曲面。通常情况下,二次曲面的拟合会比平面更好,所以牛顿法选择的下降路径会更符合真实的最优下降路径。
参考资料:
- 机器学习-周志华
- 机器学习三人行(系列五)----你不了解的线性模型(附代码)
- ML模型2:线性回归模型
- 算法实践1_线性回归
- 矩阵求导、几种重要的矩阵及常用的矩阵求导公式
- 官方文档
