李宏毅《机器学习》笔记-2.Regression

1. 什么是Regression(回归)

如果一个任务的输出（output）是一个数值（scalar），那么这种任务就是Regression（回归）。
例如：股票指数预测；无人驾驶中输出方向盘角度；商品推荐中使用者购买商品的可能性等

2. 线性回归案例：宝可梦cp值

根据宝可梦当前cp值以及一些其他指标，预测进化后的cp值

使用机器学习三板斧

Step1. 设计模型（Model）

假设进化后的cp值为y，y与进化前的cp值 $x_{cp}$ 成线性关系，则我们可以设计如下线性模型： $y=b+w\cdot x_{cp}$，其中w是权重，b是偏差。若给出不同的权重和偏差，就可以得出一堆函数 $f_1,f_2\cdots$。
若考虑多个特征（feature），则可以构建一个相对复杂的线性模型：$y=b+\sum w_i{x}_i$，这里的 $w_i$ 分别是每个 $x_i$ 对应的权重。

Step2. 判断模型好坏（Goodness of Function）

取10只宝可梦，假设真实值是 ${\hat{y}}^1\cdots {\hat{y}}^{10}$。我们需要一个额外的函数去评价真实值和预测值的好坏，这个函数成为 损失函数（Loss function）
在线性模型中，我们使用平方误差函数，即：
$$\mathrm{L}(f)=\sum _{n=1}^{10}{\left({\hat{y}}^n-f\left(x_{cp}^n\right)\right)}^2$$
也可以写成关于 w 和 b 的函数，即：
$$\mathrm{L}(w,b)=\sum _{n=1}^{10}{\left({\hat{y}}^n-\left(b+w\cdot x_{cp}^n\right)\right)}^2$$

Step3. 选择最好的函数（Best Function）

使得总损失是最小的函数就是最终想要得到的函数，通过线性代数的方法可以直接解出这个问题对应的 w 和 b
$$\begin{array}{rl}{f}^{\ast }=& \arg \underset{f}{\min }L(f)\\ w^{\ast },b^{\ast }& =\arg \underset{w,b}{\min }L(w,b)\\ & =\arg \underset{w,b}{\min }\sum _{n=1}^{10}{\left({\hat{y}}^n-\left(b+w\cdot x_{cp}^n\right)\right)}^2\end{array}$$
但对于复杂的问题，更通用的是使用 梯度下降（Gradient Descent） 方法求解。对于这个问题，梯度下降解法如下：

1. 给 w 和 b 随机选取初始值点 $w^0,b^0$
2. 计算损失函数 L 在这个点上的梯度$$\begin{gathered} \frac{\partial L}{\partial w}=\sum _{n=1}^{10}2\left({\hat{y}}^n-\left(b+w\cdot x_{cp}^n\right)\right)\left(-x_{cp}^n\right) \\ \frac{\partial L}{\partial b}=\sum _{n=1}^{10}2\left({\hat{y}}^n-\left(b+w\cdot x_{cp}^n\right)\right)(-1) \end{gathered}$$
3. 更新 w 和 b 的值，$\eta$是事先定义好的学习率 $$\begin{gathered} w^1\leftarrow w^0-\eta \frac{\partial L}{\partial w_0} \\ {b}^1\leftarrow b^0-\eta \frac{\partial L}{\partial b_0} \end{gathered}$$
4. 重复2,3步，直到 L 不再减少

简单的梯度下降并不是完美的，一般情况下很容易会遇到停滞期(plateau)，鞍点(saddle point)，局部最小值等问题。但是在线性回归里面，损失函数是凸的(convex)，所以不用考虑这些问题。

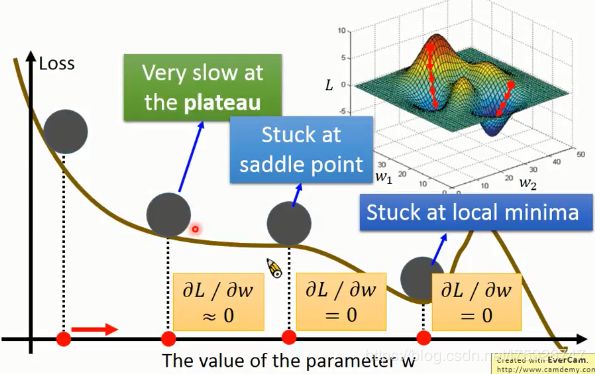
结果

对于模型$y=b+w\cdot x_{cp}$ 经过梯度下降，我们选择一个最好的函数，对应的参数为 b=-188.4, w=2.7。给出10个新的数据，此时总损失是 35.0。

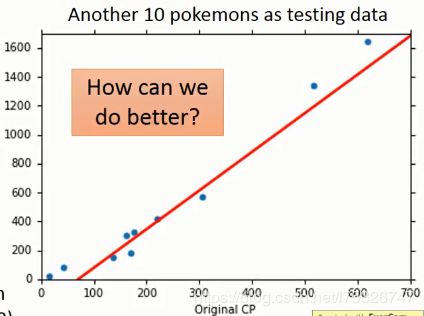
此时，尝试使用另一个模型（二次多项式模型）：$y=b+w_1\cdot x_{cp}+w_2\cdot {\left(x_{cp}\right)}^2$，求出最好的函数是 $b=-10.3,w_1=1.0,w_2=2.7\times 10^{-3}$。此时，训练样本上平方误差是 15.4，在测试样本上是 18.4。看起来比线性模型更好。
若考虑更高维的模型呢？

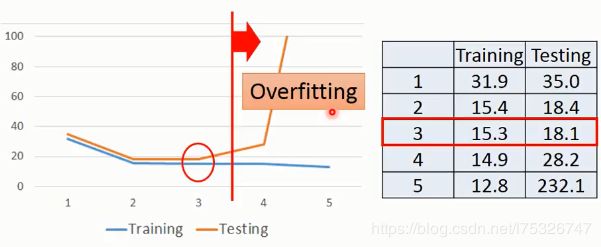
当模型越来越复杂的时候，训练样本的误差是一直变小，但是测试样本的误差后面会变大，证明出现了欠拟合（Overfitting）。

3. 如何减少过拟合

1. 收集更多的数据

这里指收集更多的样本以及特征，例如考虑宝可梦的种类、高度、重量等等。但是考虑了太多特征会造成严重的过拟合，所以还需要引入新的东西。

2. 正则化（Regularization）

在损失函数中增加惩罚因子（Regularization），使得参数w的取值更小，最终让整个函数变得更加平滑。（这里有一个假设，就是平滑的曲线更有可能是正确的，与奥卡姆剃刀原则类似）
$$L=\sum _n{\left({\hat{y}}^n-\left(b+\sum w_i{x}_i\right)\right)}^2+\lambda \sum {\left(w_i\right)}^2$$
那为什么函数w越小，函数就越平滑呢。因为当x变了一个一个很小的变化量的时候，整体的y=w∗x+b不会变化太大，所以得到的值理论上也更加准确。

结果

加入正则化后，误差随 $\lambda$ 的变化如下图所示：

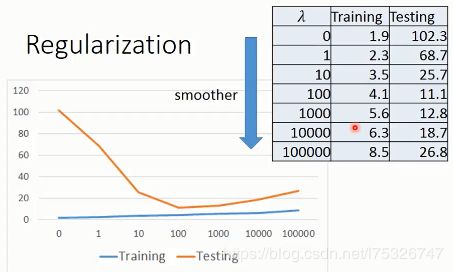
随着 $\lambda$ 的增大，训练样本的误差逐渐增大，但是测试样本的误差先减小后增大，在 100 的时候达到最小，可见这里是一个比较好的选择。