OBB generation via Principal Component Analysis

这是我在国外找到的OOB分析检测教程， 写的很好， 所以转载一下。

Bounding volumes have numerous applications in video games. In a physics engine, bounding volumes are used for broad-phase intersection tests between game objects, with the hope that their (simpler) tests reduce the number of cycles spent on more complicated and accurate intersection tests. In a graphics engine, bounding volumes are tested against the camera’s view frustum- objects that are outside the camera’s view and subsequently culled and are not drawn, saving precious time and maintaining a playable framerate.

Of the various bounding volumes used, we will focus on the oriented bounding-box, or OBB for short.

Unlike an axis-aligned bounding box (AABB), the faces of an OBB do not have to be parallel to any of the three co-ordinate planes.

It is easy to generate a bounding AABB given a set of vertices (for instance, a mesh). However, the question we’d like to ask is, given the same set of vertices, how do we generate an ideal OBB?

We will use concepts from statistics and numerical linear algebra to solve this problem.

Principal Component Analysis
When gathering data for a linear system (our OBB edges are straight), there are three possible sources of confusion:

1. Noise
2. Rotation
3. Redundancy

Noise arises from inaccuracies in our measurements, while Rotations arise from simply not knowing the true underlying variables in the system we are studying, for example, we could very well be measuring a (hopefully linear) combination of the true variables.

Finally, Redundancy arises from not knowing whether the variables we are measuring are independent, and that we may be measuring one or more (again, hopefully linear) combinations of the same set of variables.

Principal Component Analysis, or PCA is a technique that uses an orthogonal transformation (a rotation) that converts a set of observations (our vertex cloud) of possibly correlated variables, into a set of values of linearly uncorrelated variables called principal components. In doing so, it accomplishes three things with the data set:

1. Isolates noise
2. Eliminates effects of rotation
3. Separates out the redundant degrees of freedom

In statistics, the covariance between two variables measures the degree of the linear relationship between the two variables. Small values indicate that the variables are independent (no correlation).

Notice that the covariance of a variable against itself is just simply the variance of that random variable.

This then leads onto the covariance matrix, which is a matrix whose element in the (i ,j) position is the covariance between the ith and jth elements of a vector of random variables. Essentially, the covariance matrix generalizes the concept of variance to multiple dimensions.

The diagonal elements of the matrix are the variances of our variables. Large diagonal elements correspond to strong signals.
The off-diagonal elements are the covariances between our variables. Large off-diagonal elements correspond to distortions in our data.

To minimize distortion, if we redefine our variables (as linear combinations of each other), then the covariance matrix will change. In particular, we want to change the covariance matrix such that the off-diagonal elements are close to zero, hence we want to diagonalize the covariance matrix.

Notice that the covariance matrix is real-valued and symmetric, which means that we are guaranteed to have three eigenvectors in the similarity transformation (change of basis matrix) when we diagonalize.

The point is this- the eigenvectors of the covariance matrix make up the orientation of our OBB. Large eigenvalues correspond to large variances, so we should align our OBB along the eigenvector corresponding to the largest eigenvalue.

Example
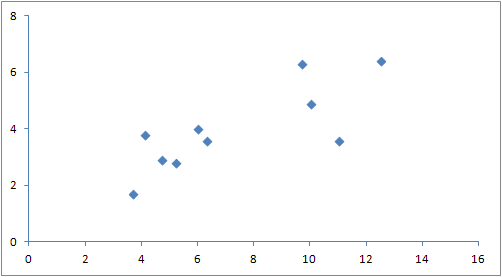
As an example, suppose we would like to generate an OBB for the following data set of ten points:

(3.7, 1.7), (4.1, 3.8), (4.7, 2.9), (5.2, 2.8), (6.0, 4.0), (6.3, 3.6), (9.7, 6.3), (10.0, 4.9), (11.0, 3.6), (12.5, 6.4)

Doing the math, we compute the variances and covariances which leads to the following covariance matrix:

This then leads to the following similarity transform:

We then use the eigenvectors for our OBB axes:

Projecting onto these vectors allow us to determine the OBB’s center and half-extent lengths, giving us the following image:

The above OBB is centered at approximately (8.10, 4.05) with half-extents of 4.96 and 1.49 units corresponding to the two axis vectors above. The span of the OBB’s axes are marked in green.

Convex hulls
One might notice in the above computation that all vertices play a role in determining the covariance matrix, when all we’re really trying to do is to compute a bounding volume. That is to say, the vertices inside the mesh still play a role in the covariance matrix, and thus the final eigenvectors, when really they shouldn’t since they’re contained by the other vertices.

For example, suppose we had a very dense point cloud concentrated locally within the mesh. Its density would skew the covariances, even though the points lie inside the mesh and would already be encapsulated by any bounding volume.

We can modify the above algorithm by instead computing the covariance matrix for the vertices that make up theconvex hull of the data set. Mathematically, the convex hull of a set is the smallest convex set that contains all of the set elements. Intuitively, the convex hull can be visualized as the shape formed when a rubber band is stretched around the points.

Alas, actually determining the convex hull of a set is one of the fundamental problems of computational geometry, and is outside the scope of this article.

Repeating the above algorithm on the convex hull leads to an OBB not very different from the one generated earlier.

The points that make up the convex hull is the set {(3.7, 1.7), (4.1, 3.8), (9.7, 6.3), (11.0, 3.6), (12.5, 6.4)}.

Our covariance matrix and subsequent diagonalization gives us:

which in turns leads to an OBB with differences beyond the accuracy of 3 significant figures. In terms of total area, the OBB generated from the convex hull is ironically larger than the one generated from the entire set by 0.000395 square units.

Personally, I don’t think such minute savings (if there even are any) in volume is worth the extra computational effort (not to mention the effort required to generate the convex hull), when the list of other things that require attention goes on. :)