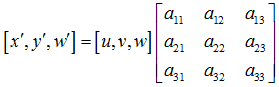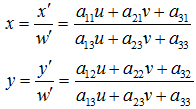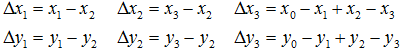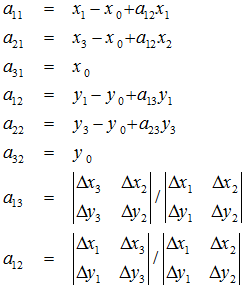opencv仿射变换和透视变换（一）理论篇

一、话说仿射变换和透视变换

对于平面区域，有两种方式的几何转换：一种是基于2×3矩阵进行的变换，叫仿射变换；另一种是基于3×3矩阵进行的变换，叫透视变换或者单应性映射。关于仿射变换和透射变换的矩阵变换，这篇博文不做重点讨论，因为图像本质就是矩阵，对矩阵的变换就是对图像像素的操作，很简单的数学知识。

仿射变换可以形象的表示成以下形式。一个平面内的任意平行四边形ABCD可以被仿射变换映射为另一个平行四边形A’B’C’D’。通俗的解释就是，可以将仿射变换想象成一幅图像画到一个胶版上，在胶版的角上推或拉，使其变形而得到不同类型的平行四边形。相比较仿射变换，透射变换更具有灵活性，一个透射变换可以将矩形转变成梯形。如下图： 

1.1 仿射变换的API

void cvWarpAffine(    const CvArr* src,//输入图像    CvArr* dst,//输出图像    const CvMat* map_matrix,//2×3变换矩阵->传个矩阵进来？    int flags=CV_INTER_LINEAR|CV_WARP_FILL_OUTLIERS,//插值方法    CvScalar fillval=cvScalarAll(0))

从上面的函数中，我们可以看到其中需要传进去一个2×3变换矩阵，因此我们在调用cvWarpAffine（）函数之前，要计算仿射映射矩阵，因此在OpenCV中有函数cvGetAffineTransform（）来计算仿射映射矩阵。

CvMat* cvGetAffineTransform(    const CvPoint2D32f* pts_src,    const CvPoint2D32f* pts_dst,//src,dst三个二维点(x,y)的数组    CvMat* map_matrix//得到的仿射映射矩阵参数)

另一个获取变换矩阵的方法

CV_EXPORTS_W Mat getRotationMatrix2D( Point2f center, double angle, double scale );

1.2 透视变换API

CV_EXPORTS Mat getPerspectiveTransform( const Point2f src[], const Point2f dst[] );

void warpPerspective( InputArray src, OutputArray dst,
                                   InputArray M, Size dsize,
                                   int flags = INTER_LINEAR,
                                   int borderMode = BORDER_CONSTANT,

                                   const Scalar& borderValue = Scalar());

1.3 二者的联系

仿射变换：二维空间的变换 ； 线性变换 ；已知3对坐标点就可以求得变换矩阵

透视变换：三维空间的变换 ； 非线性变换 ；已知4对坐标点可以求得变换矩阵
 

二、重点讲透视变换

透视变换(Perspective Transformation)是将图片投影到一个新的视平面(Viewing Plane)，也称作投影映射(Projective Mapping)。我们知道在图像的仿射变换中需要变换矩阵是一个2x3的两维平面变换矩阵，而透视变换本质上空间立体三维变换，根据其次坐标方差，要把三维坐标投影到另外一个视平面，就需要一个完全不同的变换矩阵M，所以这个是透视变换跟OpenCV中几何仿射变换最大的不同。 
OpenCV中透视变换的又分为两种：1稀疏透视变换 ，2密集透视变换

我们经常提到的对图像的透视变换都是指密集透视变换，而稀疏透视变换在OpenCV的特征点匹配之后的特征对象区域标识中经常用到。一般情况下密集透视变换warpPerspective函数常与函数getPerspectiveTransform一起使用实现对图像的透视校正。而稀疏透视变换perspectiveTransform经常与findhomography一起使用。
通用的变换公式为：

u,v是原始图片左边，对应得到变换后的图片坐标x,y,其中。
变换矩阵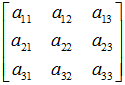可以拆成4部分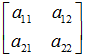，表示线性变换，比如scaling，shearing和ratotion。用于平移，产生透视变换。所以可以理解成仿射等是透视变换的特殊形式。经过透视变换之后的图片通常不是平行四边形（除非映射视平面和原来平面平行的情况）。

重写之前的变换公式可以得到：

所以，已知变换对应的几个点就可以求取变换公式。反之，特定的变换公式也能新的变换后的图片。

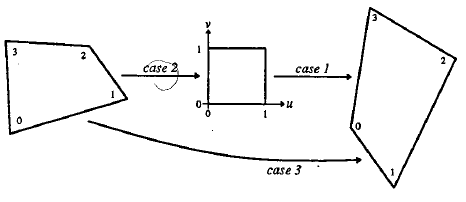
简单的看一个正方形到四边形的变换：
变换的4组对应点可以表示成：

根据变换公式得到：

定义几个辅助变量：

都为0时变换平面与原来是平行的，可以得到：

不为0时，得到：

求解出的变换矩阵就可以将一个正方形变换到四边形。反之，四边形变换到正方形也是一样的。于是，我们通过两次变换：四边形变换到正方形+正方形变换到四边形就可以将任意一个四边形变换到另一个四边形。

 opencv中相关API函数：

计算透视矩阵（通过输入和输出图像中两组点计算透视矩阵）：

findHomography( InputArray srcPoints, InputArray dstPoints,
                               OutputArray mask, int method = 0, double ransacReprojThreshold = 3 );
 

 图像的透视变换（利用透视矩阵对图像进行透视变换）：

warpPerspective( InputArray src, OutputArray dst,
                                   InputArray M, Size dsize,
                                   int flags = INTER_LINEAR,
                                   int borderMode = BORDER_CONSTANT,
                                   const Scalar& borderValue = Scalar());
 点的透视变换（利用透视矩阵对点进行透视变换）：

perspectiveTransform(InputArray src, OutputArray dst, InputArray m );
 

---

参考文献

https://blog.csdn.net/zhangjunp3/article/details/80036310

https://blog.csdn.net/qq_24946843/article/details/82697364

https://blog.csdn.net/zhangjunp3/article/details/80318533