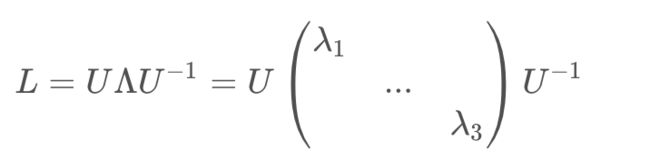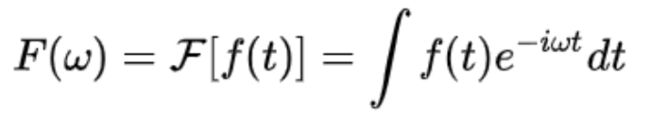图卷积网络（Graph Convolutional Network）

转载+整理：https://blog.csdn.net/qq_41727666/article/details/84622965

序 — 图简介，图卷积网络的出现。

图（graph）是一种数据格式，它可以用于表示社交网络、通信网络、蛋白分子网络等，图中的节点表示网络中的个体，连边表示个体之间的连接关系。许多机器学习任务例如社团发现、链路预测等都需要用到图结构数据，因此图卷积神经网络的出现为这些问题的解决提供了新的思路。下图就是一个简单的图结构数据：

图上的神经网络，最早由Joan Bruna于2014年在论文Spectral Networks and Locally Connected Networks on Graph中提出。图卷积网络（简称GCN），由Thomas Kpif于2017年在论文Semi-supervised classification with graph convolutional networks中提出。它为图（graph）结构数据的处理提供了一个崭新的思路，将深度学习中常用于图像的卷积神经网络应用到图数据上。

 

 

一、研究GCN的原因

1、CNN的【平移不变性】在【非矩阵结构】数据上不适用

2、希望在【拓扑图】上提取空间特征来进行机器学习

3、GCN主要工作：引入可以优化的【卷积参数】

 

二、提取【拓扑图】空间特征的两种方式

1、vertex domain(spatial domain)：顶点域（空间域）

操作：把每个顶点相邻的neighbors找出来

缺点：每个顶点的neighbors不同，计算处理必须针对每个节点

2、spectral domain：谱域

过程：

（1）定义graph上的Fourier Transformation傅里叶变换

利用Spectral graph theory，借助图的拉普拉斯矩阵(L)的特征值(λ)和特征向量研究图的性质

（2）定义graph上的convolution卷积

 

三、图的拉普拉斯矩阵

（一）定义： 拉普拉斯矩阵L 

                    L = D - A

其中，L为Laplacian矩阵；D是顶点的度矩阵（对角矩阵），对角线上的元素依次为各个顶点的度（与该顶点相连的边的条数）；A是图的邻接矩阵。

计算方法实例：

 

（二）拉普拉斯矩阵L的良好性质

1、是对称矩阵，可以进行谱分解（特征分解），与GCN的Spectral Domain对应

2、只在【中心节点】和【一阶相连的顶点】这两种位置上有非0元素，其余位置都是0

注：一阶相连就是通过一条边直接相连，如上图中与顶点1一阶相连的顶点为5和2；

二阶相连就是通过两条边相连，如上图中与顶点1二阶相连的顶点为4（1-5-4）、2（1-5-2）、5（1-2-5）、3（1-2-3）

3、可以通过拉普拉斯算子与拉普拉斯矩阵进行类比

 

（三）拉普拉斯矩阵L的谱分解（特征分解）

1、矩阵L的特征分解定义：将矩阵L分解为由特征值λ和特征向量u表示的矩阵之积

 

（1）求特征值和特征向量：λ为特征值，u为特征向量，则满足下式：

                                     

  (2）求特征分解：

 

令 L是一个 N×N 的方阵，且有 N 个线性无关的特征向量 。这样， L可以被分解为：

其中，U是N×N方阵，且其第i列为L的特征向量ui，ui为列向量；

Λ是对角矩阵，其对角线上的元素为对应的特征值。

 

2、拉普拉斯矩阵：【半正定】【对称】矩阵

 

性质：

（1）有n个线性无关的特征向量

（2）特征值非负

（3）特征向量相互正交，即Q为正交矩阵

设拉普拉斯矩阵L中，λi为特征值，ui为特征向量，U为特征向量ui作为列向量组成的方阵，那么拉普拉斯矩阵的谱分解形式为：

 

 

四、Graph上的傅里叶变换与卷积

 

（一）核心工作

把拉普拉斯算子的【特征函数】

变为

Graph对应的拉普拉斯矩阵的【特征向量】

 

（二）Graph上的傅里叶变换

1、传统傅里叶变换：

 

2、Graph上的傅里叶变换

拉普拉斯矩阵=离散拉普拉斯算子

拉普拉斯矩阵的【特征向量U】=拉普拉斯算子的【特征函数exp(-iwt)】

仿照上面传统傅里叶定义，得到Graph上的傅里叶变换：

i为第i个顶点

λl为第l个特征值；ul为第l个特征向量

f为待变换函数，f尖为其对应的傅里叶变换，f和f尖与顶点i一一对应

 

3、Graph上的傅里叶逆变换：

（三）Graph上的卷积

1、传统卷积定理：

f为待卷积函数，h为卷积核（根据需要设计）

f*h为卷积结果

关于卷积定理，需要补充详细一点：卷积定理是傅立叶变换满足的一个重要性质。卷积定理指出，函数卷积的傅立叶变换是函数傅立叶变换的乘积。具体分为时域卷积定理和频域卷积定理，时域卷积定理即时域内的卷积对应频域内的乘积；频域卷积定理即频域内的卷积对应时域内的乘积，两者具有对偶关系。

用数学式子描述一下，假设f(t)和g(t)是时域下的函数，对应F(w)与G(w)是傅里叶变换后的频域下的函数。F为福利也变换，F^(-1)是傅里叶逆变换，那么：

 时域卷积定理：F[f(t)*g(t)] = F(w)·G(w)

 

 频域卷积定理： F(w)*G(w) = 2π · F[f(t)·g(t)] 

                              F^(-1 )[F(w)*G(w)] = 2π · f(t)·g(t) 

2、Graph上的卷积：仿照上面定义

f为待卷积函数，h为卷积核（根据需要设计）

f*h为卷积结果

3、由式（1）可以看出，U为特征向量，f为待卷积函数，重点在于设计含有【可训练】【共享参数】的【卷积核h】

 

 

五、深度学习中的GCN

1、第一代GCN：

2、第二代GCN：

 

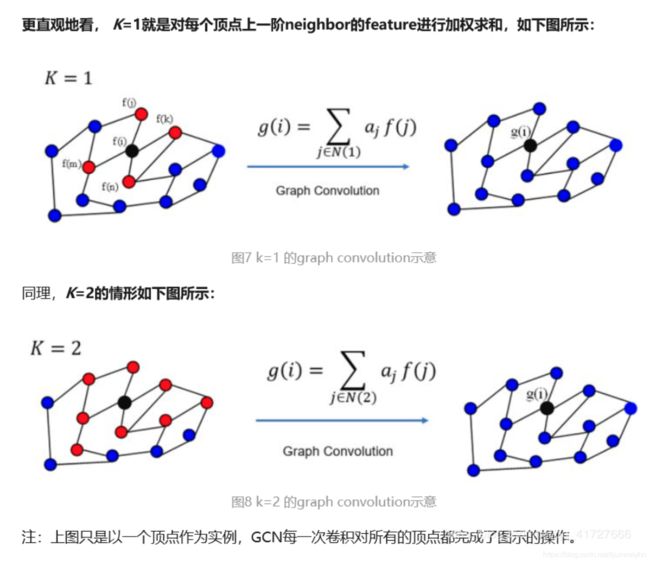
3、实例：

K=1时，对于顶点i，将顶点i以及顶点i的一阶相连顶点（j，k，m，n）的feature值（f函数值）做加权求和，权重就是参数αj，最终输出新的feature值（g函数），为提取得到的空间特征

K=2时，对于顶点i，将顶点i以及顶点i的一阶相连顶点、二阶相连顶点的feature值加权求和，输出新的feature值

 

这里问题是K=2是为什么就要包含二阶

这里补充一下L矩阵，抛开L矩阵中数字的含义，如果非0，那么一阶L中的非0值就是指的一步内能到达的，同理，2，3和高阶的L。