线性拟合和梯度下降python代码实现—面向对象（二）

最近看到了一个系列博客，写的不错，就拿来学习了下。一来加深理解，二来锻炼自己编写代码的能力。

关于基础的理论知识就不重述了，网上资源很多，这里推荐：https://www.zybuluo.com/hanbingtao/note/448086，因为我就是学习的这个系列博客。

这里只对比和上篇python 实现感知器之间的联系和代码复用的地方。
这里只更新下激活函数即可，而且这里的激活函数相当于什么也没做，原样输出，即保持线性的形式。

代码如下：

#!/usr/bin/env python
# -*- coding: UTF-8 -*-

from perceptron import Perceptron


#定义激活函数f
f = lambda x: x # 相当于原样输出

class LinearUnit(Perceptron):
    def __init__(self, input_num):
        '''初始化线性单元，设置输入参数的个数'''
        Perceptron.__init__(self, input_num, f)


def get_training_dataset():
    '''
    捏造5个人的收入数据
    '''
    # 构建训练数据
    # 输入向量列表，每一项是工作年限
    input_vecs = [[5], [3], [8], [1.4], [10.1]]
    # 期望的输出列表，月薪，注意要与输入一一对应
    labels = [5500, 2300, 7600, 1800, 11400]
    return input_vecs, labels    


def train_linear_unit():
    '''
    使用数据训练线性单元
    '''
    # 创建感知器，输入参数的特征数为1（工作年限）
    lu = LinearUnit(1)
    # 训练，迭代10轮, 学习速率为0.01
    input_vecs, labels = get_training_dataset()
    lu.train(input_vecs, labels, 10, 0.01)
    #返回训练好的线性单元
    return lu


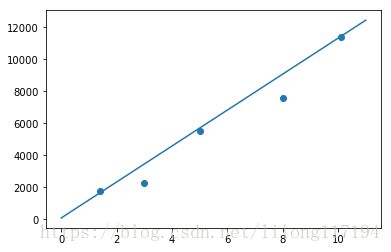
def plot(linear_unit):
    import matplotlib.pyplot as plt
    input_vecs, labels = get_training_dataset()
    fig = plt.figure()
    ax = fig.add_subplot(111)
    ax.scatter(map(lambda x: x[0], input_vecs), labels)
    # 训练得到权重和偏置
    weights = linear_unit.weights
    bias = linear_unit.bias
    x = range(0,12,1)
    y = map(lambda x:weights[0] * x + bias, x)
    ax.plot(x, y)
    plt.show()


if __name__ == '__main__': 
    '''训练线性单元'''
    linear_unit = train_linear_unit()
    # 打印训练获得的权重
    print linear_unit
    # 测试
    print 'Work 3.4 years, monthly salary = %.2f' % linear_unit.predict([3.4])
    print 'Work 15 years, monthly salary = %.2f' % linear_unit.predict([15])
    print 'Work 1.5 years, monthly salary = %.2f' % linear_unit.predict([1.5])
    print 'Work 6.3 years, monthly salary = %.2f' % linear_unit.predict([6.3])
    plot(linear_unit)

运行结果：

weights :[1124.0634970262222]
bias    :85.485289

Work 3.4 years, monthly salary = 3907.30
Work 15 years, monthly salary = 16946.44
Work 1.5 years, monthly salary = 1771.58
Work 6.3 years, monthly salary = 7167.09

模型很简单，激活函数和学习算法也很简单，但这里我觉得最大的值得学习的地方就在于面向对象编程范式的便利。

这里导入了Perceptron类：

# 这里定义一个感知器的类
class Perceptron(object):

    def __init__(self, input_num, activator):
        '''
        初始化感知器，设置输入参数的个数，以及激活函数。
        激活函数的类型为double -> double
        '''
        self.activator = activator
        # 权重向量初始化为0.0
        self.weights = [0.0 for _ in range(input_num)]
        # 偏置项初始化为0.0
        self.bias = 0.0

    def __str__(self): # __str__:类实例字符串化函数
        '''
        打印学习到的权重、偏置项
        '''
        return 'weights\t:%s\nbias\t:%f\n' % (self.weights, self.bias)

    def predict(self, input_vec):
        '''
        输入向量，输出感知器的计算结果
        '''
        # 把input_vec[x1,x2,x3...]和weights[w1,w2,w3,...]打包在一起
        # 变成[(x1,w1),(x2,w2),(x3,w3),...]
        # 然后利用map函数计算[x1*w1, x2*w2, x3*w3]
        # 最后利用reduce求和:reduce()还可以接收第3个可选参数，作为计算的初始值
        xi_wi=map(lambda (x, w): x * w,zip(input_vec, self.weights))
        # 激活函数的输入为w_1*x_1+w_2*x_2+bias
        return self.activator(reduce(lambda a, b: a + b,xi_wi , 0.0) + self.bias)

    def train(self, input_vecs, labels, iteration, rate):
        '''
        输入训练数据：一组向量、与每个向量对应的label；以及训练轮数、学习率
        '''
        # 每次迭代都把所有的样本输入
        for i in range(iteration):
            self._one_iteration(input_vecs, labels, rate)

    def _one_iteration(self, input_vecs, labels, rate):
        '''
        一次迭代，把所有的训练数据过一遍
        '''
        # 把输入和输出打包在一起，成为样本的列表[(input_vec, label), ...]
        # 而每个训练样本是(input_vec, label)
        samples = zip(input_vecs, labels)
        # 对每个样本，按照感知器规则更新权重
        for (input_vec, label) in samples:
            # 计算感知器在当前权重下的输出
            output = self.predict(input_vec)
            # 更新权重
            self._update_weights(input_vec, output, label, rate)

    def _update_weights(self, input_vec, output, label, rate):
        '''
        按照感知器规则更新权重
        '''
        # 把input_vec[x1,x2,x3,...]和weights[w1,w2,w3,...]打包在一起
        # 变成[(x1,w1),(x2,w2),(x3,w3),...]
        # 然后利用感知器规则更新权重
        delta = label - output
        self.weights = map(lambda (x, w): w + rate * delta * x,
                           zip(input_vec, self.weights))
        # 更新bias
        self.bias += rate * delta

而该类定义了

• 初始化：初始化权重、偏置、激活函数；
• 打印输出函数：打印学习到的权重和偏置
• 训练参数的类方法
• 预测的类方法
• 一次迭代的类方法（随机梯度下降）
• 更新参数的类方法

其中参数更新的递推公式是：

wnew=wold+η∑i=1n(y(i)−yˆ)x(i) w n e w = w o l d + η ∑ i = 1 n ( y ( i ) − y ^ ) x ( i )

这里的更新方式是批梯度下降，但算法里采用的是随机梯度下降，更新公式为：

wnew=wold+η(y(i)−yˆ)x(i) w n e w = w o l d + η ( y ( i ) − y ^ ) x ( i )

注意：
Python中lambda表达式
看几个例子

>>> fun = lambda x,y,z : x + y + z
>>> fun(1, 2, 3)
6
>>> fun = [(lambda n : i + n) for i in range(10)] 
>>> fun
[lambda> at 0x0000000002A43CF8>, lambda> at 0x0000000006372DD8>, lambda> at 0x0000000006372E48>, lambda> at 0x0000000006372EB8>, lambda> at 0x0000000006372F28>, lambda> at 0x0000000006372F98>, lambda> at 0x000000000637A048>, lambda> at 0x000000000637A0B8>, lambda> at 0x000000000637A128>, lambda> at 0x000000000637A198>]
>>> fun[3](4) # fun[3](4)指调用fun中第三个函数，n赋值为3,所以结果为13
13
>>> fun[4](4)
13

>>> fun = [(lambda n,i = i : i + n) for i in range(10)]
>>> fun[3](4)
7
>>> fun[4](4)
8
>>> filter(lambda x : x % 2 == 0, range(10))
[0, 2, 4, 6, 8]
>>> map(lambda x, y : x * y, range(1,4), range(1,4))  
[1, 4, 9]
>>> reduce(lambda x, y : x + y, range(10))
45
>>> 

map(lambda (x, w): x * w,zip(input_vec, self.weights))的用法
首先这里的lambda (x, w): x * w,zip(input_vec, self.weights)中的lambda (x, w)的用法要注意，这里代表的是一个参数。而正确的lmbda参数形式其实是这样的lambda x,y:x+y，x,y是它的2个形参，所以这里 lambda (x,w)其实就只有一个参数，那就是一个tuple类型的参数。
看几个例子：

In [2]: map(lambda (x, w): x * w,[(2,4),(3,6)])
Out[2]: [8, 18]

In [3]: map(lambda x, w: x * w,(2,4),(3,6))
Out[3]: [6, 24]

In [4]: map(lambda (x, w): x * w,[(2,4),(3,6)])
Out[4]: [8, 18]

In [5]: map(lambda x, w: x * w,[(2,4),(3,6)])
Traceback (most recent call last):

  File "<ipython-input-5-aec2dcefae36>", line 1, in <module>
    map(lambda x, w: x * w,[(2,4),(3,6)])

TypeError: <lambda>() takes exactly 2 arguments (1 given)

In [7]: map(lambda x, w: x * w,[2,4],[3,6])
Out[7]: [6, 24]

面向对象编程。面向对象是特别好的管理复杂度的工具，应对复杂问题时，用面向对象设计方法很容易将复杂问题拆解为多个简单问题，从而解救我们的大脑。
还有就是numpy实现了很多基础算法，对于实现机器学习算法来说是个必备的工具，这里没有使用numpy，从而对算法原理有更深入的理解。