OpenCV-3-几何变换

OpenCV-3-几何变换

3.1 图像放缩

import cv2
import numpy as np
from matplotlib import pyplot as plt

img = cv2.imread(r'F:\Blog\opencv\lena.png',cv2.IMREAD_COLOR)
print(r'origin shape:',end=''),print(img.shape)
img1 = cv2.resize(img,None,fx=2, fy=2, interpolation = cv2.INTER_CUBIC)
print(r'double shape:',end=''),print(img1.shape)
img2 = cv2.resize(img,(100,100), interpolation = cv2.INTER_AREA)
print(r'fixed shape:',end=''),print(img2.shape)

origin shape:(506, 505, 3)
double shape:(1012, 1010, 3)
fixed shape:(100, 100, 3)

这里缩放有两个比较常见的方式，一个是指定缩放倍数，一个是指定缩放大小。后面的interpolation是差值方法的选项。 官方推荐，如果要是缩小图像的话最好用cv2.INTER_AREA插值方法，如果是放大图像的话最好使用cv2.INTER_CUBIC或者cv2.INTER_LINEAR，其中cv2.INTER_CUBIC要稍微慢一点。

除此之外，还有两个比较特殊的操作，是图像金字塔操作，分别是cv2.pyrUp和cv2.pyrDown, 可以用于成倍数的模糊缩放图像，以及用于图像的合成，有兴趣可以参见手册：https://docs.opencv.org/4.1.1/dc/dff/tutorial_py_pyramids.html

涉及到的操作：cv2.resize

3.2 图像仿射变换

我们可以粗暴的把2维图像的平移，旋转，相似，都看作放射变换的特殊情况，因为都是通过在图像的坐标系统上作用一个2×3的矩阵实现的

img = cv2.imread(r'F:\Blog\opencv\lena.png',cv2.IMREAD_COLOR)
[rows,cols,chan] = img.shape

M = np.float32([[1,0,100],[0,1,50]])
img_trans = cv2.warpAffine(img,M,(cols,rows))
print(r'matrix for translation:'),print(M)

M = cv2.getRotationMatrix2D(((cols-1)/2.0,(rows-1)/2.0),90,1)
img_rotate = cv2.warpAffine(img,M,(cols,rows))
print(r'matrix for rotation:')
print(M)

pointset1 = np.float32([[20,20],[60,10],[10,200]])
pointset2 = np.float32([[5,10],[25,5],[5,80]])
M = cv2.getAffineTransform(pointset1,pointset2)
img_pair = cv2.warpAffine(img,M,(cols,rows))
print(r'matrix for paired points:')
print(M)

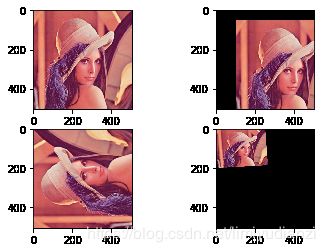
plt.subplot(2,2,1),plt.imshow(cv2.cvtColor(img,cv2.COLOR_BGR2RGB))
plt.subplot(2,2,2),plt.imshow(cv2.cvtColor(img_trans,cv2.COLOR_BGR2RGB))
plt.subplot(2,2,3),plt.imshow(cv2.cvtColor(img_rotate,cv2.COLOR_BGR2RGB))
plt.subplot(2,2,4),plt.imshow(cv2.cvtColor(img_pair,cv2.COLOR_BGR2RGB))
plt.show()

matrix for translation:
[[   1.    0.  100.]
 [   0.    1.   50.]]
matrix for rotation:
[[  6.12323400e-17   1.00000000e+00  -5.00000000e-01]
 [ -1.00000000e+00   6.12323400e-17   5.04500000e+02]]
matrix for paired points:
[[ 0.50704225  0.02816901 -5.70422535]
 [-0.02816901  0.38732394  2.81690141]]

这里要注意的是affine变换中，最后一个给的大小的参数是输出图像的大小，顺序和我们正常img.shape输出的顺序相反，一定要格外注意。

为了较为清楚的表述矩阵中不同的参数对结果有什么影响，我这里用一张别的地方找到的图片来说明（个人觉的很清楚）。

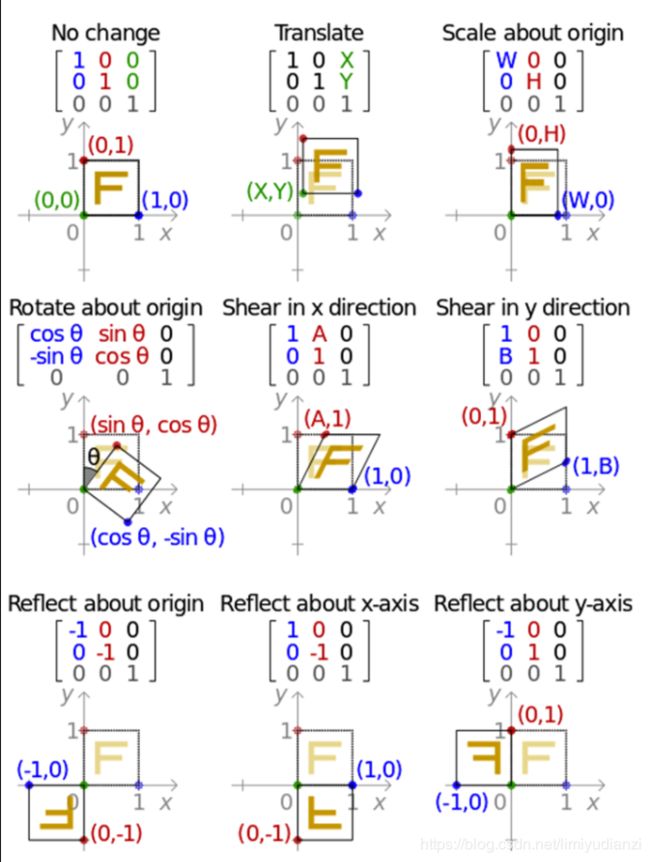
另外这里展示了三种方法来构建变换的矩阵，第一个平移的例子中，我们人为设计矩阵，这种方法还是有一定难度的，尤其是在问题变得复杂的时候。第二个是cv2.getRotationMatrix2D的方法，其中第一个参数是旋转的中心，（x,y）的形式表示，第二个参数是旋转的角度，正值表示逆时针旋转，最后一个规定scale，这里scale是1所以不做尺度上的缩放。第三个是通过传入点集进行仿射变换矩阵的计算，这种方法适合用于图像的配准，实现计算两张图具有相同特征的点进行图像的仿射变换。

涉及到的指令有：cv2.warpAffine， cv2.getRotationMatrix2D， cv2.getAffineTransform

3.3 投影变换

img = cv2.imread(r'F:\Blog\opencv\lena.png',cv2.IMREAD_GRAYSCALE)
[rows,cols] = img.shape
pointset1 = np.float32([[56,65],[368,52],[28,387],[389,390]])
pointset2 = np.float32([[0,0],[300,0],[0,300],[300,300]])
M = cv2.getPerspectiveTransform(pointset1,pointset2)
dst = cv2.warpPerspective(img,M,(cols,rows))
print(r'matrix for projective:')
print(M)
plt.subplot(1,2,1),plt.imshow(img, cmap='gray')
plt.subplot(1,2,2),plt.imshow(dst, cmap='gray')
plt.show()

matrix for projective:
[[  1.05587376e+00   9.18151097e-02  -6.50969128e+01]
 [  4.69010049e-02   1.12562412e+00  -7.57920240e+01]
 [  1.83251448e-04   5.13337001e-04   1.00000000e+00]]

投影变换是更加复杂的变换，保证了直线还是直线。我们看到这里是用九个参数来定义的投影变换。同时实现投影变换使用cv2.warpPerspective， 计算旋转矩阵使用的是cv2.getPerspectiveTransform。具体使用的方法都和上面的例子一样。

涉及到的操作有：cv2.warpPerspective， cv2.getPerspectiveTransform