如何提高文本生成任务中的文本多样性

1. 引言

    在文本生成任务中，经典模型Seq2Seq虽然取得了很大的进步，但是由于其目标函数采用的是极大似然估计，即：
$$1/|\mathcal{S}|\sum _{(T,S)\in \mathcal{S}}\log p(T|S)$$其中，$S$表示给定的输入句子，$T$表示输出句子。因此，会导致一个问题，即生成的句子一般是训练集中比较高频的回复，这样的回复虽然是比较安全的，但是却会使得回复变得平淡无奇，缺乏多样性。因此，很多学者对该模型进行改进，希望可以提高文本生成的多样性，从2015年以来，提高文本多样性的方法大致可以分为四类：

• 第一类：采用新的模型对Beam Search得到的候选序列进行重排，比如MMI-bidi等。
• 第二类：引入内容的形式，对输出文本先预测一个关键词，然后对其进行补全，比如Seq2BF等。
• 第三类：直接修改Beam Search算法，对每个时间步的条件概率施加多样性惩罚，比如MMI-antiLM、diverseRL、DBS等。
• 第四类：直接修改训练时的损失函数，比如ITF-loss等

本文将对这些方法进行汇总和对比。

2. MMI-antiLM、MMI-bidi方法

    为了使得生成的句子更加多样性，李纪为博士等人（2015）采用了最大互信息（Maximum Mutual Information，MMI）作为目标损失函数，在一定程度上提高了文本生成的多样性和趣味性。

论文地址：《A Diversity-Promoting Objective Function for Neural Conversation Models》

2.1 MMI-antiLM、MMI-bidi损失函数

    在文本生成任务中，令$S$表示给定的输入句子$S=\left\{s_1,s_2,\dots ,s_{N_s}\right\}$，其中，$N_s$表示输入句子的词汇数量，即句子的长度，令$T$表示输出句子$T=\left\{t_1,t_2,\dots ,t_{N_t},EOS\right\}$，$N_t$表示输出句子的词汇数量，即句子的长度，则MMI目标损失函数可以表示为：
$$\log \frac{p(S,T)}{p(S)p(T)}$$这样一来，损失函数不仅仅考虑了输入句子，还考虑输出句子的出现频率，因此，不会偏袒于那些高频率的回复。该损失函数可以进一步表达为：
$$\hat{T}=\underset{T}{\mathrm{argmax}}\{\log p(T|S)-\log p(T)\}$$可以发现，其实MMI损失函数可以看成是在极大似然估计的基础上，添加了一项对输出句子概率的惩罚项，用更通用的形式可以表达为：
$$\hat{T}=\underset{T}{\mathrm{argmax}}\{\log p(T|S)-\lambda \log p(T)\}$$其中，$\lambda$为惩罚参数，表示高频率回复的惩罚。作者将这种目标函数记为MMI-antiLM。根据贝叶斯公式，有：
$$\log p(T)=\log p(T|S)+\log p(S)-\log p(S|T)$$将该式代入目标函数有：
$$\begin{array}{rl}\hat{T}& =\arg \underset{T}{\max }\{(1-\lambda )\log p(T|S)+\lambda \log p(S|T)-\lambda \log p(S)\}\\ & =\arg \underset{T}{\max }\{(1-\lambda )\log p(T|S)+\lambda \log p(S|T)\}\end{array}$$作者将这种目标函数记为MMI-bidi。

2.2 如何使用

    在真实的训练过程中，如果直接将MMI-antiLM和MMI-bidi两种损失函数作为训练时的损失函数，那么训练将会非常艰难，会导致语法紊乱和解码难的问题，因此，作者在真实训练过程中，还是采用极大似然估计作为模型训练的损失函数，但是在预测时才采用MMI损失函数。

    对于MMI-antiLM损失函数，我们知道，当$\lambda$比较大时，此时损失函数会减弱第一项的权重，导致生成的句子会出现一些语法上的错误，特别是当句子比较长时，当$\lambda$设置比较小时，作者发现该问题还是会出现。我们知道，对于decoder，每一个词的输出都依赖于前面词汇的输出和encoder得到的语义向量，但是，随着句子长度的增长，encoder的语义向量对后面词语的影响会慢慢减弱，因此，输出句子的通顺程度到了后面主要还是依赖于语言模型而不是输入句子，那么，对于后面词语的生成，其实可以不采用多样性惩罚，因此，对于MMI-antiLM损失函数中的$p(T)$项，作者在实际使用时进行了如下改进：
$$U(T)=\prod _{k=1}^{N_t}p\left(t_k|t_1,t_2,\dots ,t_{k-1}\right)\cdot g(k)$$其中，$g(k)$表示对输出句子每一个词语的权重，其计算公式如下：
$$g(k)=\{\begin{array}{ll}1& \text{ if }k\le \gamma \\ 0& \text{ if }k>\gamma \end{array}$$其中，$\gamma$为一个阈值参数，表示当长度大于该值后，则将对应的$p(T)$项置为0，也就是说对生成句子后面的词语不施加多样性惩罚，多样性只取决于前面几个词汇。这样一来，MMI-antiLM的损失函数可以改写为：
$$\log p(T|S)-\lambda \log U(T)$$
    另外，作者在真实应用时，还加入句子长度作为另一项正则项，即：
$$Score(T)=p(T|S)-\lambda U(T)+\gamma N_t$$其中，$\gamma$表示惩罚参数。

    对于MMI-bidi损失函数，我们知道其实就是$\log p(T|S)$和 $\log p(S|T)$两项之间的加权平均，因为在推理时，作者在训练时，分成两个Seq2Seq模型进行训练，即先训练一个输入句子$S$到输出句子$T$的Seq2Seq模型，记为$mode{l}_1$，然后训练一个输出句子$T$到输入句子$S$的Seq2Seq模型，记为$mode{l}_2$。接着，对于一个输入句子$S$，会使用$mode{l}_1$通过Beam_search先生成$N_{best}$个候选的句子，然后利用$mode{l}_2$计算每个候选句子的 $\log p(S|T)$，最后根据计算结果对200个候选句子进行重排，从而提高输出句子的多样性。

3. Seq2BF方法

    2016年，北大Lili Mou等人提出了一种新的方法，即Seq2BF模型，该模型的基本思想是在decoder之前，先根据点态互信息（Pointwise Mutual Information，PMI）计算出一个与输入句子最相关的名词，作为输出句子的关键词，然后采用两个Seq2Seq模型分别对该词的前文和后文进行decode补全，最后作为预测的输出句子。

论文地址：《Sequence to Backward and Forward Sequences: A Content-Introducing Approach to Generative Short-Text Conversation》

3.1 关键词预测

    在关键词预测这一步，作者采用了PMI作为计算指标，记输入句子中的每一个词汇为$w_q$，输出句子中的每一个词汇为$w_r$，则PMI的计算公式如下：
$$\mathrm{PMI}\left(w_q,w_r\right)=\log \frac{p\left(w_q,w_r\right)}{p\left(w_q\right)p\left(w_r\right)}=\log \frac{p\left(w_q|w_r\right)}{p\left(w_q\right)}$$在预测时，对于一个输入句子$w_{q_1},\cdots w_{q_n}$，计算输出句子词汇列表中每个词汇与输入句子的PMI分数，然后从中选择分数最高的词汇作为预测的关键词$w_r^{\ast }={\mathrm{argmax}}_{w_r}\mathrm{PMI}\left(w_{q_1}\cdots w_{q_n},w_r\right)$，一般会限制该关键词为名词，具体的计算公式如下：
$$\begin{gathered} \mathrm{PMI}\left(w_{q_1}\dots w_{q_n},w_r\right)=\log \frac{p\left(w_{q_1}\cdots w_{q_n}|w_r\right)}{p\left(w_{q_1}\cdots w_{q_n}\right)} \\ \approx \log \frac{{\prod }_{i=1}^{n}p\left(w_{q_i}|w_r\right)}{{\prod }_{i=1}^{n}p\left(w_{q_i}\right)}=\sum _{i=1}^n\log \frac{p\left(w_{q_i}|w_r\right)}{p\left(w_{q_i}\right)}=\sum _{i=1}^n\mathrm{PMI}\left(w_{q_i},w_r\right) \end{gathered}$$该近似计算假设$p\left(w_{q_i}\right)$和$p\left(w_{q_i}|w_r\right)$都是独立的。

3.2 Seq2BF模型

    当关键词预测出来后，因为要将关键词包含在输出句子中，此时没法直接使用Seq2Seq模型，因此，作者在Seq2Seq模型的基础上进行了稍微修改，提出了Seq2BF模型。对于给定的输入句子$\mathbf{q}=q_1{q}_2\cdots q_n$和输出句子$\mathbf{r}=r_1{r}_2\cdots r_m$，我们知道传统的Seq2Seq模型是最大化如下的条件概率：
$$p\left(r_1,\cdots ,r_m|q\right)=p\left(r_1|q\right)p\left(r_2|r_1,q\right)\cdots p\left(r_m|r_1\cdots r_{m-1},q\right)=\prod _{i=1}^{m}p\left(r_i|r_1\cdots r_{i-1},q\right)$$假设输出句子的关键词为$r_k$，则此时输出句子可以被分解为前后两个子句子，即：
$$\begin{array}{ll}\text{ Backward sequence: }& r_{r-1},\cdots ,r_1\\ \text{ Forward sequence: }& r_{k+1},\cdots ,r_m\end{array}$$这样一来，原先的条件概率可以转化为：

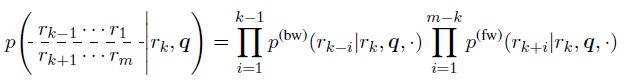
在具体的建模过程中，作者提出了三种模式的Seq2BF模型：①sep-B/F（分离Seq2BF）：即对于前向和后向两个子句子分别采用两个生成器进行生成；②syn-B/F（同步Seq2BF）：对于前向和后向两个子句子采用一个单层的RNN同时进行decode，但是采用不同的输出层进行输出。③asyn-B/F（异步Seq2BF）：先采用一个解码器对后向句子进行解码，然后解码后将句子进行反向排序并与关键词拼接，然后作为另一个解码器的前缀输入，一直解码直到句子结束。作者在实验中发现采用第三种类型的Seq2BF模型效果最好，该模型的整体结构如下图所示：

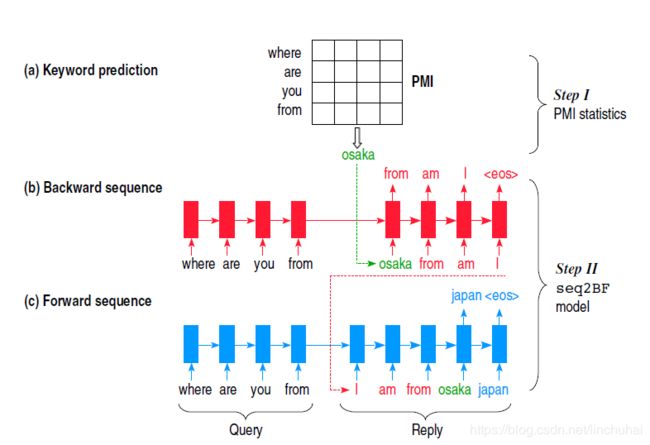
    需要注意的是，在训练阶段，关键词的选择采用的是随机选取的方法，而在预测阶段，则采用PMI分数最高的词汇作为关键词。

4. diverseRL方法

    2016年，李纪为博士在15年那篇的基础上又进行了改进，这次，他直接对Beam_search方法进行修改，使得Beam_search的搜索结果多样性更强，并且其通用性更强，可以迁移到很多其他的任务上。在参数的选择方面，引进了强化学习的思想，使得该方法更加灵活。

论文地址：《A Simple, Fast Diverse Decoding Algorithm for Neural Generation》

4.1 Diverse Beam_search

    对于一个输入句子$X$和输出句子$Y$，传统的Beam_search方法会根据$p(Y|X)$选择$K$个最优的候选生成句子，其中，$K$为beam_size的取值。其思想如下：在时间步$t-1$，编码器会保存当前$K$个最优的已解码序列$Y_{t-1}^k=\left\{y_1^k,y_2^k,\dots ,y_{t-1}^k\right\},k\in [1,K]$以及他们的概率$S\left(Y_{t-1}|X\right)=\log p\left(y_1,y_2,\dots ,y_{t-1}|X\right)$，然后在第$t$个时间步时，Beam_search会对每个已解码序列进一步解码其后面的第$t$个词汇，对每个序列同样选择$K$个候选的词汇$y_t^{k,k^{\prime }},k^{\prime }\in [1,K]$，这样一来，总共会产生$K\times K$个新的候选序列：
$$\left[Y_{t-1}^k,y_t^{k,k^{\prime }}\right],k\in [1,K],k^{\prime }\in [1,K]$$他们的概率计算如下：
$$S\left(Y_{t-1}^k,y_t^{k,k^{\prime }}|x\right)=S\left(Y_{t-1}^k|x\right)+\log p\left(y_t^{k,k^{\prime }}|x,Y_{t-1}^k\right)$$然后根据这$K\times K$候选序列的概率大小，从中选择$K$个概率最大的候选序列作为当前时间步的候选序列，然后重复该过程一直到解码结束。具体的如下图所示：

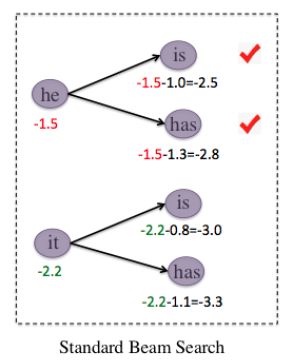
    可以发现，虽然Beam_search在每个时间步都会选择$K$个候选序列，但是每一步都会受到上一步的影响，当$K$个父节点的概率相差比较大时，随着句子长度的增加，后续的$K$个后续序列往往会集中到个别父节点上，如上图最开始的候选序列是‘he’和‘it’，但是到了第二步后，此时概率最大的两条候选序列都集中在’he’节点，从而导致最终出来的$K$个候选序列都是比较相似的。因此，Diverse Beam_search对概率公式进行了简单的修正，在后面添加了一项惩罚项，即：
$$\hat{S}\left(Y_{t-1}^k,y_t^{k,k^{\prime }}|x\right)=S\left(Y_{t-1}^k,y_t^{k,k^{\prime }}|x\right)-\gamma k^{\prime }$$其中，$k^{\prime }$为每个候选序列在同一个父节点下的排序，$\gamma$为超参数，称为Diversity rate。具体如下图所示：

    这样一来，每一条候选序列都会受到内部排序的影响，因此那些在每个父节点排名靠前的序列会更容易进入到最终的候选序列，从而使得生成的候选序列更加多样性。

4.2 Diversity rate的选择

    由于Diverse Beam_search引入了一个超参数$\gamma$，对于不同的输入文本，该值应该是能够自动调整而不是固定为一个设定的值，因此，作者引入了强化学习的思想，当生成器训练好之后，会将模型的参数固定，然后设定一个$\gamma$的候选集合$\Gamma$，并将每种选择进行参数化$h_{{\gamma }^{\prime }}$，接着，对于每一个输入$X$，会通过encoder将其转化为一个向量表示$h_X$，然后通过softmax计算当前输入在各个候选$\gamma$值上的概率分布：
$$\pi \left(\gamma (X)={\gamma }^{\prime }|X\right)=\frac{\exp \left(h_X^T\cdot h_{{\gamma }^{\prime }}\right)}{{\sum }_{j=1}^{j=|\Gamma |}\exp \left(h_X^T\cdot h_{{\Gamma }_j}\right)}$$选择其中概率最大的$\gamma$作为当前输入的$\gamma$，然后采用Diverse Beam_search选择出最好的输出文本，最后，在整个验证集上计算每个输出文本的Bleu值作为奖励函数，记为$R\left(\gamma (X)={\gamma }^{\prime }\right)$，然后寻求一种最优的策略，使得最终的期望奖励值最大化：
$$E_{\pi \left(\gamma (X)={\gamma }^{\prime }|X\right)}\left[R\left(\gamma (X)={\gamma }^{\prime }\right)\right)]$$从而对参数进行更新：
$$\nabla E(\theta )=[R(\gamma (X)-b]\nabla \log \pi \left(\gamma (X)={\gamma }^{\prime }|X\right)$$

5. Diverse Beam Search方法

   &ebsp;2018年，Ashwin K Vijayakumar等人也提出了一种新的Diverse Beam Search，简称DBS，该方法的大致思想是：将原先的Beam Search均分为$G$个组，每个组含有$B^{\prime }=B/G$条候选路径，对每个组还是按照Beam Search的思想进行解码，但是每个组在解码时还要考虑解码后的序列与前面每个组已经解码的序列之间的差异性。作者将该方法与李纪为博士的diverseRL方法、传统的Beam Search方法进行对比，发现在多个任务上都有效提升了文本生成的多样性。

论文地址：《DIVERSE BEAM SEARCH: DECODING DIVERSE SOLUTIONS FROM NEURAL SEQUENCE MODELS》

5.1 DBS原理介绍

    在decoder时，每一步的输出概率都取决于其输入$x$和前面的输出序列$y_{t-1},\dots ,y_1$，记在第$t$个时间步的对数概率为：$\theta \left(y_t\right)=\log \mathrm{Pr}\left(y_t|y_{t-1},\dots ,y_1,\mathbf{x}\right)$，为了简化计算，将每一步的对数概率$\theta (\cdot )$记为$y_t$。由前面我们知道，Beam Search在每次解码时，都会从所有解码序列中选择概率最大的前$B$条候选序列作为最终的输出序列，但是因为Beam Search的搜索方式很容易导致最终生成的$B$条序列都集中在某几个父节点，从而导致最终的$B$条输出序列有大部分都是非常接近的。因此，为了克服这个问题，DBS在每次解码时，在原先的概率公式上添加了一项差异项$\Delta \left(Y_{[t]}\right)$，用来衡量后续序列之间的多样性或差异性。如果直接在Beam Search的基础上对每个序列计算两两之间的多样性，那么，该计算的复杂度将是$|\mathcal{V}{|}^B$，其中$|\mathcal{V}|$表示decoder的词汇数量，这在实际中将是不可行的。因此，DBS将原先的Beam Search的$B$个候选序列分为了$G$个组，然后依次对每个组采用Beam Search进行解码，对每个组进行解码时，都要确保前面的组固定不变，然后将当前组与前面的组计算多样性，因为此时计算序列的多样性只考虑当前组与前面组已经解码好的后续序列，因此，计算的复杂度大大降低，该形式也因此被称为双贪婪（doubly greedy）的形式。

    记$Y_{[t]}$表示Beam Search在$t$时刻的$B$个候选序列，将其分为$G$个组$Y_{[t]}^g,g\in [G]$，此时，每个组就相当于Beam size为$B^{\prime }=B/G$。DBS对每一组进行解码时，会在原先概率公式的基础上添加一项差异项$\Delta \left({\mathrm{y}}_{[t]},Y_{[t]}^g\right)$，表示当前序列与第$g$组的候选序列的差异性，其计算公式如下：
$$\Delta \left({\mathrm{y}}_{[t]},Y_{[t]}^g\right)=\sum _{b=1}^{B^{\prime }}\delta \left({\mathrm{y}}_{[t]},{\mathrm{y}}_{b,[t]}^g\right)$$其中，$\delta (\cdot ,\cdot )$表示序列差异性的度量，其计算方式有多种，一会再讲。因此，每一组在每个时间步挑选出来的$B^{\prime }$个候选序列可以表示为：

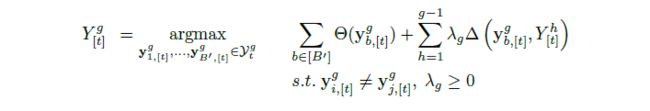
该方法即为DBS方法。具体的算法过程如下：

5.2 相关参数设置

    通过前面的介绍我们知道，DBS引入了一些超参数的设置，比如组数$G$、惩罚参数$\lambda$、差异性度量函数$\delta (\cdot ,\cdot )$。作者在实验过程中，对这几个参数也分别进行了调优，并发现：

• 随着组数$G$的增加，DBS的精度会不会提高，将组数$G$设置为$B$，即$G=B$效果是最好的。
• $\lambda$不宜过高或过低，一般设置在0.2~0.8效果比较好。
• 对于差异项度量函数$\delta (\cdot ,\cdot )$，作者对比了Hamming diversity、Cummulative diversity、n-gram diversity和Neural-embedding diversity四种计算方式，发现采用Hamming diversity效果相对比较好，该方法直接度量每个句子与其他组句子词汇使用的差异性。

6. ITF-loss方法

    前面介绍的方法中，其实都是在模型训练结束后，对decoder方式进行改动而成的，而Ryo Nakamura等人在2018年提出的ITF-loss则直接改动训练时的MLE损失函数，该方法非常简单，不需要额外地训练其他模型，很容易迁移到各种模型当中。

论文地址：《Another Diversity-Promoting Objective Function for Neural Dialogue Generation》

6.1 ITF-loss原理介绍

    在传统的Seq2Seq中，我们一般会采用Softmax Cross Entropy（后文简记为SCE）作为损失值的计算函数，其表达式如下：
$$L_{\mathrm{s}\mathrm{c}\mathrm{e}}=-\log \left(\frac{\exp \left(x_c\right)}{{\sum }_{k=1}^{|V|}\exp \left(x_k\right)}\right)$$其中，$x_k$表示第$k$个单词的输出值，$x_c$表示真实值的输出值，$|V|$表示输出词汇的数量。ITF-loss在训练时，对SCE损失函数施加了一个权重，其计算方式如下：
$$\begin{array}{rl}{L}_{\mathrm{I}\mathrm{T}\mathrm{F}}& =w_c{L}_{\mathrm{s}\mathrm{c}\mathrm{e}}\\ w_c& =\frac{1}{\mathrm{f}\mathrm{r}\mathrm{e}\mathrm{q}{\left({\text{ token }}_c\right)}^{\lambda }}\end{array}$$其中，$w_c$表示真实值对应的权重，与该真实值的词频刚好成反比，这样一来，对于那些高频的词汇，会使得他们的损失值越小，而对于低频的词汇，则会使得他们的损失值越大，从而使得模型更关注那些低频的词汇的损失，其实该方法与focal loss非常类似。

6.2 推理阶段的ITF-loss

    在推理阶段，同样可以对每一步的输出施加一个权重，其计算方式如下：
$$y=\mathrm{argmax}\{\log \mathrm{softmax}(w\odot x)\}$$其中，$w$的计算方式与训练时权重的计算方式一样。但是作者在实验中发现，采用这样的ITF-loss进行推理时，会出现一些句子重复的情况，因此，在推理时，对权重的计算进行了如下修改：
$$suppressor\left(x_k\right)=\frac{1}{{\left\{1+\text{ count }\left({\text{ token }}_k\right)\right\}}^{\lambda }}{x}_k$$其中，$\text{ count }({\text{ token }}_k)$表示词汇${\text{ token }}_k$在当前的已解码出的序列中出现的次数。这样有效抑制了重复句子的出现。

7. 总结

    最后做一下总结吧：

• MMI两种损失函数与传统的极大似然估计相比的话，可以提高文本生成的多样性和趣味性。
• MMI-antiLM不需要额外训练一个模型，使用起来会方便一点。
• MMI-bidi需要训练两个模型，训练时间翻了一倍，另外，对于最终输出句子的重排，其实还是受到Seq2Seq生成的候选句子的限制，如果生成的候选句子多样性差，那么就算重排之后，其实也不一定能提高多样性。
• Seq2BF虽然通过预测关键词来提高文本生成的多样性，但是因为其关键词都限定为名词，而我们知道，有些回复其实是不包含名词的，此时如果强制要求回复必须包含预测的名词，那可能会出现错误。

参考文献

1. A Diversity-Promoting Objective Function for Neural Conversation Models.
2. Sequence to Backward and Forward Sequences: A Content-Introducing Approach to Generative Short-Text Conversation.
3. A Simple, Fast Diverse Decoding Algorithm for Neural Generation.
4. DIVERSE BEAM SEARCH: DECODING DIVERSE SOLUTIONS FROM NEURAL SEQUENCE MODELS.
5. Another Diversity-Promoting Objective Function for Neural Dialogue Generation.