Mode-Adaptive Neural Networks for Quadruped Motion Control 论文
图1.我们的方法所产生的四足动画结果。 我们展示了一些不同的四足动作模式,从左往右依次是坐姿,转圈小跑,踱步,慢跑,跳跃和站立。 这些运动步态不是逐一标记的,而是由运动速度的控制自然产生的。
摘要
动物的四足动作包括各种步态,如散步,步伐,小跑和跑步,以及诸如跳跃,坐姿,转身和怠速等动作。应用现有的特性控制框架来解决动物的四足运动问题需要大量的数据及繁琐的数据预处理,例如动作的标注和对齐等。在本文中,我们提出了一种新型的神经网络架构,称为模式自适应神经网络,用于控制动物的四足运动特性。该系统由运动预测网络和门控网络组成。给定前一帧的运动状态和用户提供的控制信号,运动预测网络会计算出当前每一帧的运动特性状态。而门控网络通过选择和混合专家权重来动态地更新运动预测网络的权重值,每个专家权重都对应特定的动作。为了提高灵活性,系统通过学习一致的专家权重值,以端到端的方式,从非结构化的角度来捕捉各种非定期/定期行动动作数据。另外,用户的控制信号是由不同步态、不同阶段中的复杂标记提供的。我们表明这种体系结构适合编码多模态的四足运动及实时动作响应的合成。
简介
四足动画是计算机动画领域中未解决的关键问题之一。它与电脑游戏和电影等应用特别相关,同时也是机器人领域一个具有挑战性的话题。通过动画来制作四足动物时,动画师 (animator) 必须通过特殊的训练来设计各种复杂的动作。本质上,这种动作复杂性是来自于四足动物的多种运动形式。如图2所示,一些诸如步行,踱步,小跑,慢跑,跑步等运动模式,它们的躯干和四肢部分都随着运动而发生复杂的变化。
据我们所知,先前的研究工作没有基于数据驱动的方式来构建系统的四足运动控制器。造成这个困难原因是上面提到的复杂性,以及四足运动控制的数据采集。因此,所捕获的数据通常缺乏结构化,所包含的随机动作并不是一个接一个地进行着。当使用这些非结构化数据设计动作特性控制器时,工程师需要手动或半自动地提取步态周期,通过数据转换将不连续的动作缝合在一起,并调整运动树及有限状态机的参数。
最近,基于神经网络的运动控制研究表明使用明确的周期来为双足动物运动提供高质量动画的方法是可行的 [Holden et al. 2017]。但是,这种框架无法应用于四足动物的运动控制,因为无法定义单一阶段中四条腿在不同的脚步模式间的过渡步态。这也使得手动对四足运动的非结构化数据进行复杂的步态标记变得不切实际。
在本文中,我们提出了一种新型网络体系结构,称为模式自适应神经网络 (MANN)。它可以从大量的非结构化四足运动数据中学习一个运动控制器。该系统由运动预测网络和门控网络组成。给定前一帧的运动状态和用户提供的控制信号,运动预测网络会计算出当前每一帧的运动特性状态。而门控网络通过选择和混合专家权重来动态地更新运动预测网络的权重值,每个专家权重都对应特定的动作。这个架构具有足够的灵活性,以便系统能够学习一致的专家权重值,来捕捉大量的非定期/定期行动动作数据。由于所捕获的非结构化四足运动数据必须将不同步态类型沿着时间轴对齐,因此,我们的框架能够大大缓解开发者进行复杂而繁琐的动作数据标记工作。此外,我们的模型不需要为不同步态给定标签,从而节省了数据预处理过程中对步态错位的处理时间。
图2.生成不同四足运动模式下的足迹 [Huang et al. 2013]。 横条表示每条腿站立的阶段。 图像的右边表示步态周期中一系列的脚印。
这篇论文的贡献可概括如下:
- 我们构建了第一个基于数据驱动的四足运动特性控制器,这种系统可以合成不同运动模式及其过渡状态间的高质量动画。
- 我们提出一种新颖的、端到端的神经网络结构,它能够从非结构化四足动作中捕捉数据,而不需要任何阶段和运动步态的标签。
- 我们将所构建的四足运动特性控制器与现有的方法进行了全面地评估对比。
模型系统
我们的系统是一个时间序列模型,给定前一个帧的状态 x 和用户的控制信号,模型可以预测当前每一帧的运动特性状态 y。为了产生各种各样的周期性和非周期性的四足运动特性,我们提出了一种新型的神经网络,称为模式自适应神经网络的结构 MANN (如下图3所示,详见原文章节6)。当前每一帧的运动由运动预测网络得到 (如下图3右,详见原文第6.1节),其网络权重是通过一个门控结构的神经网络结构 (如下图3左,详见原文第6.2节) 来动态地计算获取。门控网络收到一个动作特征 ( x 的子集),并计算专家权重的混合系数 (如下图3中),其中每一个权重都是为特定的动作训练而准备的。
为了准备训练所需的数据集,我们首先预处理狗的运动数据集并为这些数据添加标签 (详见原文第4节),然后准备网络的输入和输出矢量 (详见原文第5节)。在训练期间,整个网络一端到端的方式训练整个数据集 (详见原文第7节)。在运行期间,系统使用前一帧的运动状态和用户提供的控制信号,能够实时地展现当前每一帧中运动特性的动画 (详见原文第8节)。
图3.由门控网络和运动预测网络组成的神经网络结构体系。 门控网络以当前脚端部的效应器速度,期望的速度和动作矢量作为输入。 运动预测网络将前一帧的动作姿势和运动轨迹作为输入,并预测当前每一帧更新后的姿势和轨迹。
数据准备
为了后续研究的进行,这里我们介绍下动作捕捉和动作分类阶段所要用到的数据。
狗的动作捕捉。我们的动作捕捉数据由非结构化的狗的动作捕捉数据组成,整个数据长度为30分钟,包括各种运动模式,如散步,踱步,小跑和慢跑等,以及其他类型的动作,如坐着,站立,怠速,躺着和跳跃。数据的大小通过镜像进行双倍放大。运动数据通过平坦地面上的设施采集得到的,如下图4。这是一个由27块骨头构成的骨架模型,它总共有81自由度,非常适用于数据采集工作。
图4. 实验用到的构模型的骨架结构。它由27块骨头,总计81自由度构成。
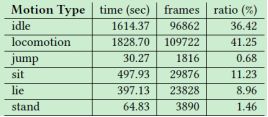
动作分类。首先,将动作类型分为运动,坐着,站着,怠速,躺着、跳跃等等。在运行阶段,用户可以通过指定某个运动类型标签来控制动作特性。这个过程是手动完成的,但想自动化实现这个过程也并不困难,因为这些动作类型中的每一种动作都具有独特性。关于动作数据的具体比率可以参见下表1。
表1. 狗的动作训练数据集的细分。这个数据集包含原始的和镜像得到的狗动作捕捉数据,这些都是未结构化的数据。
运动模式。在我们的论文中,我们专门研究四种运动模式的类型:步行,踱步,小跑和慢跑。虽然我们的系统不需要在运行时为运动模式打上控制标签,但是我们分析了数据集中数据分布的模式。由于复杂的运动过渡状态和一些模棱两可的情况,将数据分类为不同的运动模式是一件相对困难的操作。首先,基于速度曲线,我们对运动模式进行大致的分类,然后手动地将它们归入相应的模式。最终,速度与其运动模式的可视化关系结果如图5所示。这种相关性与 Coros 等人在2011年提出的模型完美匹配。
四足动作控制的模式自适应神经网络模型
运动预测网络
运动预测网络表示为 Θ(·),它是一个简单的三层神经网络,通过接收先前帧中的运动特性状态 x 并输出当前每一帧的运动特性 y。其数学表达式如下:
其中网络 α 的参数由 α= {W0∈Rh×n,W1∈Rh×h,W2∈Rm×h,b0∈Rh,b1∈Rh,b2∈Rm} 所定义。此外,这里的 h 表示网络中隐藏层所用的单元数,我们的模型把它设为512。网络的激活函数采用指数型的修正线性单元 (ReLU) [Clevert et al. 2015],其数学表达式如下:
![]()
神经网络的权重值 α 是通过混合 K 个专家权重计算得到的,β= {α1,...,αK},其中每一个都是神经网络的权重配置:α = ∑PKi = ωiαi。K 是一个元参数,它可以根据训练数据的复杂程度和大小进行调整。ω = {ω1,...,ωK} 是门控网络计算得到的混合系数,门控网络的详细计算过程可参见原文第6.2节。此外,我们发现 K = 4 足以产生高质量的运动效果,具体的讨论内容可参见原文第8节。
门控网络
门控网络表示为 Ω (·),它是一个三层的神经网络。基于给定的输入 x,它可以计算混合系数 ω,其数学表达式如下:
![]()
其中 ∈R19是 x 的子集,x 表示脚端速度效应器,当前动作标量和期望动作速度的特性。网络参数 μ= {W’0∈Rh’×19,W’1∈Rh’×h’,W’2∈RK×h’,b0∈Rh’,b1∈Rh’,b2∈RK},其中h’是隐藏层的单元数量,我们把它设置为32。σ(・) 是一个 softmax 算子,用于归一化输入以使得它们相加的和为1,这是为了进一步线性混合所必需的操作。
我们已经以多种不同的输入测试了我们的模型,包括完整的 x,效应器位置,它们的位置和速度的组合,以及旋转,并明确地发现这些功能单独运行时会产生最好的结果。这可能是运动阶段速度的强相关性导致的,产生一个类似效应,正如 [Holden et al. 2017] 研究中所提到的避免不同阶段运动间的混合理论。理想的情况下,网络可以从输入中学习信息特征,尽管由于我们的数据量相对较少,这可能会导致我们的训练过程变得很困难。但与此同时,我们观察到使用动作变量和期望值速度能够有助于提高动作特性的可控性和响应性。
模型训练
整个网络使用处理后的动作捕获数据,以端对端的方式进行训练。每个帧的输入 x 和 y 被堆叠成矩阵形式:X = [x1x2 ...],Y = [y1y2 ...]。我们使用它们的均值和标准差,对这些值平移和缩放操作,以便标准化数据。由于慢跑和小跑数据量非常有限,我们对这些动作的数据复制11次,这有助于增强我们模型的鲁棒性。
训练网络的目标是对于给定的一组输入 X,我们可以产生相应的输出变量 Y。这是一个典型的回归任务,目的是求取预测值和真实值之间的均方误差,其数学表达式如下所示:
![]()
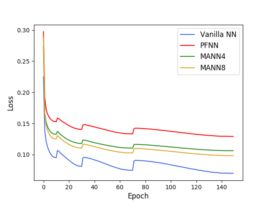
借助 Tensorflow 深度学习框架,我们部署了模型的训练过程。我们使用 AdamWR 技术中的随机梯度下降算法,这是由 Loshchilov 和 Hutter 提出的能够自动计算损失函数关于 β 和 μ 导数的一种优化技术。正如 AdamWR 算法在优化过程中所做的正则化一样,我们使用两个参数 Ti和 Tmul来控制学习率 η 和权重衰减率 λ 的下降和重启动,其初始值设置为 η= 1.0×10-4和 λ= 2.5×10-3。Ti 表示第i次运行/重新启动时的迭代总数,其初始值设为10。在每次重启动时,Ti 都乘上一个因子 Tmul = 2,即Ti + 1 = 2Ti。我们总共进行150次迭代,因此重启动过程一共发生3次,分别在第11次,第31次和第71次迭代。在训练期间,我们使用大小为32的小批量数据反复迭代,每个批量中的训练样本都是随机选择的。我们使用 Dropout 技术,其保留概率设为0.7。 整个训练过程使用4或8个专家网络,在 NVIDIA GeForce GTX 970 GPU上运行了20或30个小时。下图5显示了不同方法的学习曲线,请注意较低的训练损失或测试损失不一定对应于更高质量的运动。
图5. Vanilla neural network,PFNN 和 MANN 网络的学习曲线。我们分别采用4或8个专家权重。AdamWR 的重启动分别发生在第11次,第31次和第71次迭代,导致模型的损失增加。
实验结果及展望
在实验阶段,我们设置了不同的运动特性控制方案,在运行过程中交互式地查看不同运动特性控制的结果。我们通过与现有方法 (vanilla feedforward neural networks and phase-functioned neural networks (PFNN)) 比较,来评估我们的系统在运动质量,足部滑动伪影,腿部僵硬度及运动响应等性能,评估结果如下表2,表3,表4所示。我们还进一步研究了专家的激活权重,并在运动期间抑制它分析专家权重的功能特性。
表2.使用NN,PFNN 和 MANN 模型,以4或8个专家权重所得到的所有腿部真实的平均滑行数据。
表3. 使用 vanilla NN,PFNN 和 MANN 模型,以4或8个专家权重所得到的所有腿部每个关节真实的平均角度更新
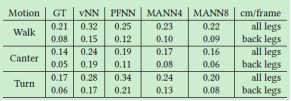
表4. 使用 vanilla NN,PFNN 和 MANN 模型,沿着预定义的不同曲线轨迹所得到的平均位置和角度偏差数据。
虽然实验结果展示了出色的性能及其系统优越性,但是我们的系统仍存在一些局限性,如时间序列模型的学习,稀疏数据库的构建以及数据库局限性等,我们将在未来的工作中进一步探讨这些问题。除了我们提出的方法以外,对于四足运动动画领域,还有几个有趣的方向值得进一步研究,如重定向不同的四足动物大小和形态,计算生成对抗运动的损失并用于优化,复杂的动态障碍环境下的四足运动控制研究等。