深入解读相机矩阵

在这片文章里，你将了解到以下内容：
1、相机的针孔模型
2、相机矩阵的概念
3、相机内参的含义
4、相机外参的含义

1 相机针孔模型

针孔模型是相机成像的基础模型，是理解后续相机矩阵内容的基础。
下图描述了基本的小孔成像过程：

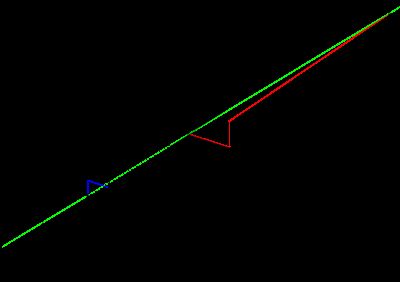
图中，X坐标系是针孔所在坐标系，Y坐标系为成像平面坐标系，P为空间一点，小孔成像使得P点在图像平面上呈现了一个倒立的像。

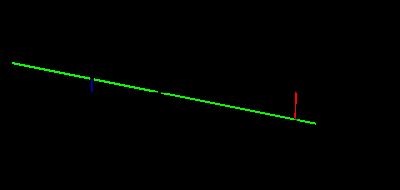
这幅图是前一幅图的俯视图，由三角相似关系可以得到：
，
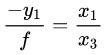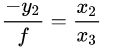
写成矩阵的形式：

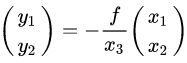
多了一个讨厌的负号（小孔成像上下颠倒，左右也颠倒），为了方便，大家把成像平面移到了和物体（P点）相同的一边，这样相似关系中就没有负号。

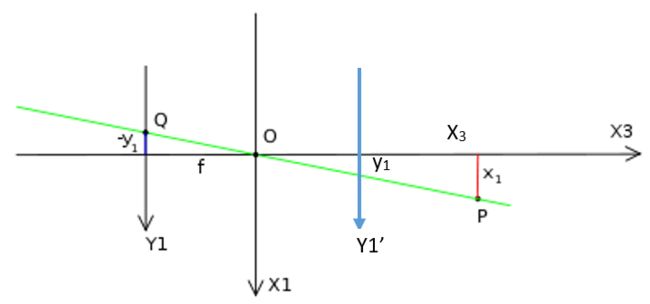
上图中Y1’为移动后的成像平面，这与移动前的比例关系是等效的。

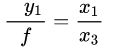
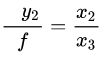
写成矩阵形式：

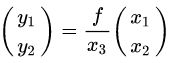
参考资料4中有一幅图能够更好的反映小孔成像的原理（下图）：

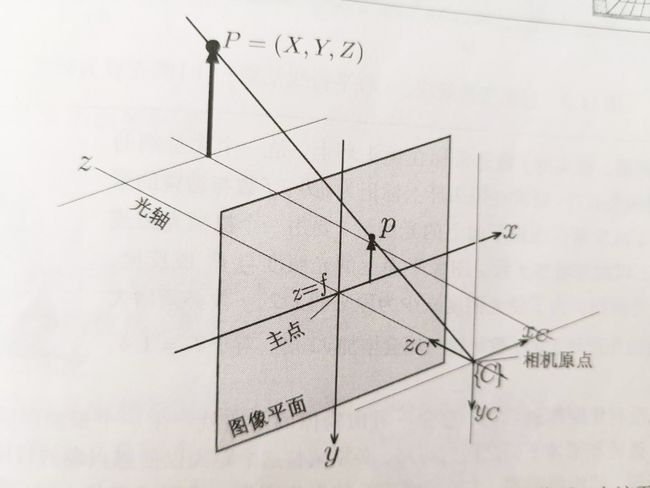
图中，
相机原点就是成像小孔；
图像平面移到了物体这一边；
图像平面距离小孔的距离为f，小孔本不存在焦距，但是实际中相机都用镜片（透镜模型和小孔模型可以认为是近似的），因此，图像平面在焦距处是清晰成像的条件。
光轴是垂直通过图像平面和相机原点的轴线，它与图像平面的交点被称为主点。
看懂了这幅图，小孔成像也就可以翻篇了。

2、什么是相机矩阵（camera matrix ）

首先来理解一下相机成像的本质：成像过程就是三维空间坐标到二维图像坐标的变换，这是一个投影过程（降维打击）。
相机矩阵就是建立这种三维到二维的投影关系。

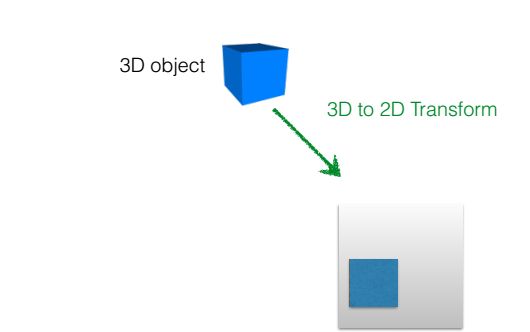
如果我们用[xw yw zw ]来表示一个空间点的坐标，用[x y]来表示对应于成像平面上的一个图像点的坐标（不是像素坐标），那么这两个点肯定是有一种变换关系联系起来的，我们把这个变换关系记为P，

但是大家都喜欢用齐次坐标，那我们就用齐次坐标来表示上述这两个点（齐次坐标有优点：可以将旋转和平移用一种统一的格式来描述）。
空间点：，图像点：
则有：
这里面，是一个3X4的矩阵（这是为了满足4X1变换到3X1的要求），该矩阵就被称为相机矩阵（camera matrix ），或者相机投影矩阵（camera projection matrix）。

上述相机矩阵只是一种非常粗略的表达，要是考卷上你写这个答案估计得不了分，实际上我们可以在细化一下该矩阵的表达。这就要再来看看小孔模型。
第一部分说小孔模型时没有使用齐次坐标，现在我们用齐次坐标再来看看小孔模型。
还记得这个表达式吧：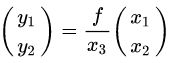
把它写成齐次形式：

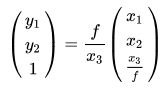
注意，左边变为[y1 y2 1]的齐次形式了，右边矩阵的第三行是额外添加的，它是等式成立的配平项。
在此，我们先暂时舍弃比例因子f/x3，只建立[y1 y2 1]与[x1 x2 x3]的关系，可以得到表达式

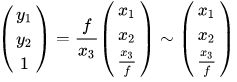
由于舍弃了一个比例因子，等式不再成立，因此使用~来表示二者之间的相似关系。
对于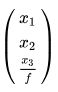，可以建立与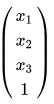的关系，用矩阵表示如下：

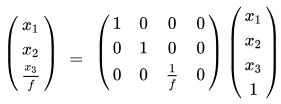
到此，就建立了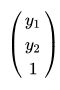与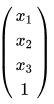的关系，如下所示：

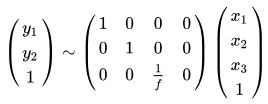
注意，不是等号。

其中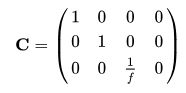，就是相机矩阵，或者乘以一个系数f写为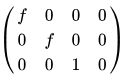可以看出，比之前的表达式具体多了。

为什么上述关系不使用等号？
因为空间三维点的齐次坐标到二维图像点的坐标不满足一 一映射的条件，空间->图像是1对1的，图像->空间是1对多的，这就意味着远处一个大的物体和近处一个小的物体在图像上投影也许是一样的，上述舍弃的那个比例因子，就是这种缩放平移关系。

上述推导来自Wikipedia，在有些版本的推导中，图像点的齐次坐标和空间点的其次坐标建立关系时，使用等式相连,，那就请注意，他们在表述图像点齐次坐标的时候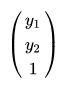，齐次项写的应该不是1，可能前面还有系数，请注意不同版本的不同表达，各种表达是等价的。

我们现在已经知道，相机矩阵的形式为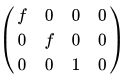而且这个矩阵是可以分解的，分解结果为这个分解结果留着后面有用。
但这个关系还远远不够，我们得接着往下走。

3、什么是内参矩阵（Intrinsic matrix）

说内参矩阵之前，还得再引入像素坐标系的概念。
上述图像点的表示是长度单位，不是像素，由于我们拿到的图像是以像素来衡量的，因此还需要将图像坐标系转化为像素坐标系。
在此直接给出结论：

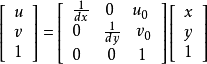
具体参见百度百科：https://baike.baidu.com/item/像素坐标/5372225
于是之前的相机矩阵又得添加一项：
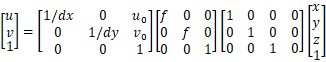（1）
上述推导中有一个假设前提，就是相机的感光元件是正方形的，感光元件的安装也是通过光轴中心的，但这不可能，于是会出现以下两个问题：
1、感光元件的基本单元不是方的，一个方形物体可能最后成像为一个矩形（甚至会有斜切效果，一般可以不考虑斜切因素）；
这导致表达式（1）中，dx与dy不相等，
2、感光元件的中心与光轴通过的主点不重合，会使得正常投影的图像发生了一点小小的位移。
这导致表达式（1）中，u0与v0可能并不等于成像传感器长宽尺寸的一半。（理想状态下就是一半）

表达式（1）中，等式右边的前三个矩阵合并，得到下式：

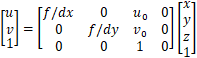
，其中被称为内参矩阵（Wikipedia）
或者只合并等式右边前两个矩阵，得到下式：

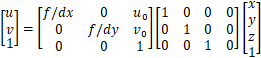
于是也有习惯将称为内参矩阵（少了一列0），都是一个意思。
内参矩阵的参数含义：
f：焦距，单位毫米，dx：像素x方向宽度，单位毫米，1/dx：x方向1毫米内有多少个像素
f/dx：使用像素来描述x轴方向焦距的长度
f/dy：使用像素来描述y轴方向焦距的长度
u0,v0,主点的实际位置，单位也是像素。

内参矩阵反应了相机自身的属性，各个相机是一不一样的，需要标定才能知道这些参数。

4、什么是外参矩阵（ extrinsic matrix）

外参矩阵是世界坐标系到相机坐标系的变换。既然是变换，我们就能够将其表达为[R t],齐次形式为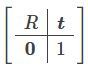
但是目前为止好像并没有在相机矩阵中看到外参矩阵。之前的相机矩阵表示如下：
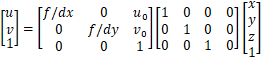（2）
那是因为，之前的推导中，我们默认世界坐标系和相机坐标系是重合的。在小孔成像模型中，空间一点的坐标被描述为[x y z 1]，这个点的坐标系原点在小孔，而相机的坐标中心也在小孔，但是在实际应用过程中，世界坐标系和相机坐标系往往不重合，这样才带来了外参矩阵的概念，下图展示了相机坐标系与世界坐标系不重合时的情况，我们只知道P点在世界坐标系下的坐标，因为要运用小孔成像原理，我们想知道P点在相机坐标系下的坐标，相机外参矩阵就实现了这种变换。

还是空间某个点p，其在世界坐标系下表示为[xw,yw,zw,1]，在相机坐标系下表示为[xc,yc,zc,1]，那么它们具有如下关系：

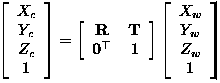
带入到相机矩阵表达式中可以得：

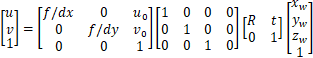
合并等式右边2、3两个矩阵：

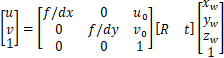
到此，我们就看到了一个比较常见的内外参数矩阵的写法，等式右边，第一个矩阵为内参矩阵（3x3），第二个矩阵为外参矩阵（3x4），合起来就是相机矩阵，它建立了三维点齐次坐标到二维点齐次坐标的变换。

争议讨论

外参矩阵常备误解为相机坐标系到世界坐标系的变换（刚好反了），等效的误解表达为：相机在世界坐标系下的位置姿态。
争议来源1：Wikipedia

争议来源2：一个讲的比较细的国外网站http://ksimek.github.io/2012/08/22/extrinsic/

争议来源3：国内很多博客，基本上都是翻译上述两句话，就不贴图了。

也许是我没理解清楚，但上述这些表述很有误导性。

我认为准确的表述应该是：
外参矩阵是世界坐标系在相机坐标系下的描述（或者位置姿态）
等价于外参矩阵是从世界坐标系到相机坐标系的变换
它确实也确定了相机在世界坐标系下的位置姿态，但相机位置姿态是外参矩阵的逆。
再说细一些：
R的每一个列向量表示世界坐标系的每一个坐标轴在相机坐标系下的指向；
t表示世界坐标系原点在相机坐标系下的表示。

依据1：自相矛盾的Wikipedia

依据2：还是上面讲的比较细的那个国外网站http://ksimek.github.io/2012/08/22/extrinsic/

该网站还详细推导了外参矩阵与相机位姿的关系，这更说明外参矩阵与相机位姿不是一回事，如下图。

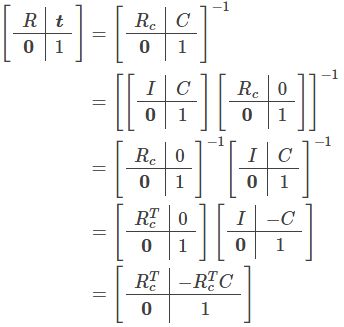
依据3：

不过上述所有资料来源都一致的讲到：外参矩阵是世界坐标系在相机坐标系下的描述，或者将世界坐标系下的点转换到相机坐标系下，这应该没有异议，其余说法的准确性自行甄别吧。

以上是我对相机矩阵的理解，欢迎讨论。

参考资料：
1、wikipedia：camera-matrix https://en.wikipedia.org/wiki/Camera_matrix
2、wikipedia：Camera resectioning https://en.wikipedia.org/wiki/Camera_resectioning
3、国外的一份PDF课件 http://www.cs.cmu.edu/~16385/s17/Slides/11.1_Camera_matrix.pdf
4、《机器人学、机器视觉与控制——Matlab算法基础》