算法设计与分析：leetcode "Two Sum"问题快速算法分享

1. 题目内容

原题：https://leetcode.com/problems/two-sum/description/

Given an array of integers, return indices of the two numbers such that they add up to a specific target.

You may assume that each input would have exactly one solution, and you may not use the same element twice.

Example

Given nums = [2, 7, 11, 15], target = 9,
Because nums[0] + nums[1] = 2 + 7 = 9,
return [0, 1].

题目要求我们从给出的数组中找出唯一的一对整数，使得其和等于target值，并且不能重复使用数组的同一个元素。

2. 题目分析

该题目相对简单，最简单粗暴的办法就是用循环遍历数组，对数组的每一个元素再通过循环来寻找和它配对的另一个元素，直到找到一对解即得到了结果。但这种方法一个明显的缺点就是需要用到两层循环，时间复杂度为 O(n2) O ( n 2 ) 。如果我们能够避免使用多余的一层循环来寻找配对元素，那么就可以将复杂度降低了。不如直接上代码：

//golang 实现，4ms,时间复杂度O(n)
func twoSum(nums []int, target int) []int {
    //用于记录配对信息，map[pairID(一对解中较小的数)]在数组中的下标
    pairs := make(map[int]int)
    var results []int 
    for index,value := range nums {
        //计算当前元素value的配对元素
        temp := target - value
        var min int
        //temp和value的较小值
        if temp < value {
            min = temp
        } else {
            min = value
        }
        //若该对中的一个元素已经存在
        if v,ok := pairs[min]; ok  {
            //判断当前值是否配对
            if nums[v] + value != target {
                continue
            }
            results = append(results,index)
            results = append(results,v)
            return results
        } else {
            pairs[min] = index
        }
    }
    return nil
}

//c++实现，8ms
class Solution {
public:
    vector<int> twoSum(vector<int>& nums, int target) {
        map<int,int> pairs;
        vector<int> result;
        int size = nums.size();
        for (int i = 0;i < size;i++) {
            int temp = target - nums[i];
            int min;
            if (temp < nums[i]) {
                min = temp;
            } 
            else {
                min = nums[i];
            }
            map<int,int>::iterator iter = pairs.find(min);
            if (iter != pairs.end()) {
                if (nums[pairs[min]] + nums[i] != target) {
                    continue;
                }
                result.push_back(pairs[min]);
                result.push_back(i);
                return result;
            }
            else {
                pairs[min] = i;
            }
        }
    }
};

该算法的运行效果不错，运行时间在leetcode所有的提交中相对比较快

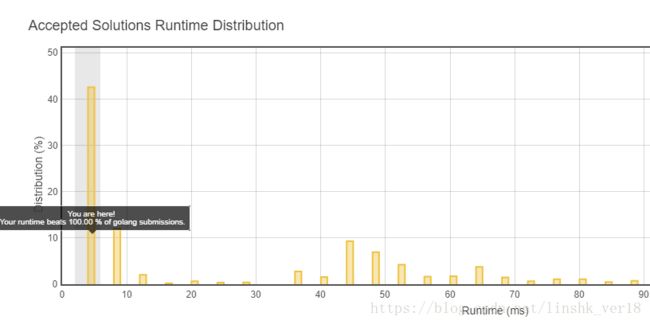
考虑到target值是给定的，因此当前元素的配对元素也是可以直接确定的，我们需要确认的就是那个配对元素是否包含在数组中。例如给定数组[2,7,11,15] 和 target值26，然后对数组进行遍历，遍历到2的时候我们需要确认26 - 2是否在数组中，遍历到11的时候需要确认15是否在数组中。

算法中用pair来表示任何一对解，对于给定的target，我们总是可以用pair中最小（或最大）的数来唯一地标识该pair的状态。例如target为10，(2,8),(3,7)等等均是pair，在数组中遍历到2的时候，用map[2] = index来表示该pair有一个数已经找到，当遍历到8或再次遍历到2 的时候检查map[2]的值是否存在，若存在则说明pair(2,8)其中一个数已经找到了。

3.小结

对于匹配问题，在遍历过程中适当的记录下遍历到的信息往往可以提高效率，避免重复的遍历。