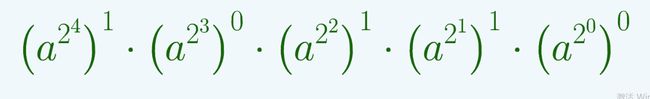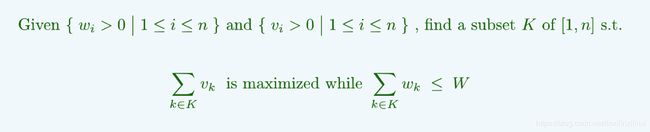ACM动态规划基础篇
文章目录
- 1 前言
- 1.1 什么是动态规划
- 1.2 什么时候要用动态规划
- 2 斐波那契数列 $Fibonacci$
- 2.1 引入
- 2.2 定义
- 2.3 递归分治解决 $Recursion$
- 2.3.1 代码
- 2.3.2 时间复杂度分析
- 2.4 解决方案
- 2.5 记忆化搜索
- 3 快速幂
- 3.1 问题描述
- 3.2 十进制快速幂
- 3.3 二进制快速幂
- 3.4 代码实现
- 4 最短向上路径问题
- 4.1 问题描述
- 4.2 暴力?
- 4.3 递归分治VS动态规划
- 4.3.1 递归分治
- 4.3.1.1 时间复杂度
- 4.3.1.2 记忆化搜索
- 4.3.2 正儿八经的动态规划
- 4.3.2.1 记忆化?
- 4.3.2.2 动态规划
- 5 最长曼哈顿路径问题
- 5.1 问题描述
- 5.2 问题分析
- 5.2.1 考虑见神杀神的记忆化搜索
- 5.2.2 考虑一路高歌猛进的动态规划
- 6 小结
- 7 最长公共子序列
- 7.1 问题描述
- 7.1.1 子串 $Substring$
- 7.1.2 子序列 $Subsequnce$
- 7.1.3 举个栗子
- 7.2 样例及其分析
- 7.3 解决问题
- 7.3.1 相同则减而治之
- 7.3.2 不同则分而治之
- 7.4 转移方程
- 7.5 dp表
- 7.6 思考题
- 8 背包问题(推荐 背包九讲)
- 8.1 01背包问题
- 8.1.1 选还是不选,这是一个问题
- 8.1.2 分析转移方程
- 8.1.3 dp表
- 8.1.4 代码实现
- 8.2 完全背包问题
- 8.3 多重背包问题
- 9 最长不降子序列LIS
- 9.1 定义
- 9.2 问题描述
- 9.3 解决问题
- 9.3.1 $O(n^2)$的算法
- 9.3.2 $O(nlogn)$算法
1 前言
1.1 什么是动态规划
动态规划(Dynamic Programming)是求解决策过程最优化的数学方法。把多阶段过程转化为一系列单阶段问题,利用各阶段之间的关系,逐个求解,创立了解决这类过程优化问题的新方法——动态规划。
1.2 什么时候要用动态规划
如果要求一个问题的最优解(通常是最大值或者最小值),而且该问题能够分解成若干个子问题,并且小问题之间也存在重叠的子问题,则考虑采用动态规划。
能采用动态规划求解的问题的一般要具有3个性质:
- 最优化原理
如果问题的最优解所包含的子问题的解也是最优的,就称该问题具有最优子结构,即满足最优化原理。 - 无后效性
即某阶段状态一旦确定,就不受这个状态以后决策的影响。也就是说,某状态以后的过程不会影响以前的状态,只与当前状态有关。 - 有重叠子问题
即子问题之间是不独立的,一个子问题在下一阶段决策中可能被多次使用到。(该性质并不是动态规划适用的必要条件,但是如果没有这条性质,动态规划算法同其他算法相比就不具备优势)
2 斐波那契数列 F i b o n a c c i Fibonacci Fibonacci
2.1 引入
有一头母牛,它每年年初生一头小母牛。每头小母牛从第二个年头开始,每年年初也生一头小母牛。请问在第n年的时候,共有多少头母牛?
2.2 定义
f i b ( n ) = f i b ( n − 1 ) + f i b ( n − 2 ) fib(n) = fib(n - 1) + fib(n - 2) fib(n)=fib(n−1)+fib(n−2)
0 0 0 1 1 1 1 1 1 2 2 2 3 3 3 5 5 5 8 8 8 13 13 13 21 21 21 34 34 34
2.3 递归分治解决 R e c u r s i o n Recursion Recursion
2.3.1 代码
int fib(n){
return (n < 2) ? n : fib(n - 1) + fib(n - 2);
}
int fib(n){
if(n < 2) return n;
return fib(n - 1) + fib(n - 2);
}
2.3.2 时间复杂度分析
T ( n ) = T ( n − 1 ) + T ( n − 2 ) + 1 > 2 ⋅ T ( n − 2 ) + 1 = O ( ( 2 ) n ) T(n) = T(n - 1) + T(n - 2) + 1 \gt 2 \cdot T(n - 2) + 1 = O((\sqrt{2})^n) T(n)=T(n−1)+T(n−2)+1>2⋅T(n−2)+1=O((2)n)
T ( n ) = T ( n − 1 ) + T ( n − 2 ) + 1 = O ( f i b ( n ) ) = O ( Φ n ) T(n) = T(n - 1) + T(n - 2) + 1 = O(fib(n)) = O(\varPhi ^ n) T(n)=T(n−1)+T(n−2)+1=O(fib(n))=O(Φn)
Φ = 1 + 5 2 = 1.618... \varPhi = \frac{1 + \sqrt{5}}{2} = 1.618... Φ=21+5=1.618...
Φ 36 ≈ 2 25 \varPhi^{36} \approx 2^{25} Φ36≈225
Φ 5 ≈ 10 \varPhi^{5} \approx 10 Φ5≈10
2.4 解决方案
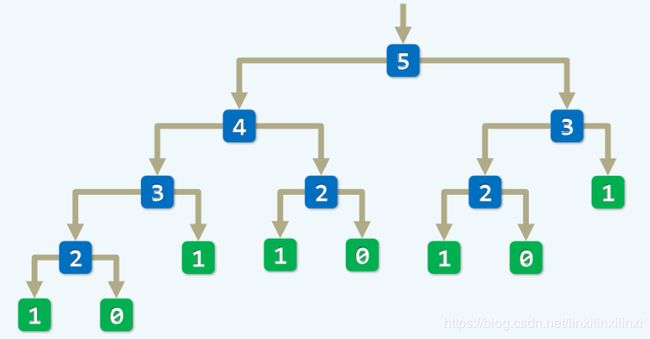
刚刚递归算法的不足之处在于重复计算了大量相同的子问题,浪费了大量时间
好记性不如烂笔头
记忆化搜索 M e m o i z a t i o n Memoization Memoization
备忘录 L o o k − u p Look-up Look−up T a b l e Table Table → \to → A r r a y Array Array
用一个数组记录需要重复计算的子问题
这就是动态规划的第一种实现方式,也是最容易理解的写法:记忆化搜索
2.5 记忆化搜索
const int maxn = 1e6 + 5;
int f[maxn];
void init(){
memset(f, -1, sizeof(f));
f[0] = 0;
f[1] = 1;
}
int fib(n){
int& ret = f[n]
if(ret != -1) return ret;
ret = fib(n - 1) + fib(n - 2);
return ret;
}
3 快速幂
3.1 问题描述
a 98765 = ? ? ? a^{98765} = ??? a98765=???
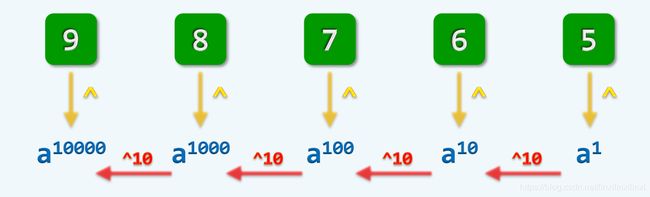
3.2 十进制快速幂
a 9 ⋅ 1 0 4 + 8 ⋅ 1 0 3 + 7 ⋅ 1 0 2 + 6 ⋅ 1 0 1 + 5 ⋅ 1 0 0 a^{9\cdot10^4 + 8\cdot10^3 + 7\cdot10^2 + 6\cdot10^1 + 5\cdot10^0} a9⋅104+8⋅103+7⋅102+6⋅101+5⋅100
( a 1 0 4 ) 9 ⋅ ( a 1 0 3 ) 8 ⋅ ( a 1 0 2 ) 7 ⋅ ( a 1 0 1 ) 6 ⋅ ( a 1 0 0 ) 5 (a^{10^4})^9 \cdot (a^{10^3})^8 \cdot (a^{10^2})^7 \cdot (a^{10^1})^6 \cdot (a^{10^0})^5 (a104)9⋅(a103)8⋅(a102)7⋅(a101)6⋅(a100)5
3.3 二进制快速幂
根据计算机的储存特性,我们可以通过以二进制的快速幂来节省代码量,以及加快运算速度
3.4 代码实现
ll quick_pow(ll a, ll b, ll mod){
ll ret = 1;
while(b){
if(b&1) ret = (ret*a)%mod;
a = (a*a)%mod;
b >>= 1;
}
return ret;
}
4 最短向上路径问题
4.1 问题描述
SPU(Shortest Path Upward)
在某一个非负整数构成的 n × m n \times m n×m矩阵中,找出从最底层通往最高层的一条路径,使得路径总长(沿途所经整数的总和)最小(你只能走到上一层离你当前位置最近的三个位置)
4.2 暴力?
如果直接暴力枚举所有的路径
分析一下,时间复杂度大概是 O ( n ⋅ 3 m ) O(n\cdot3^m) O(n⋅3m)
可能,不太行
4.3 递归分治VS动态规划
4.3.1 递归分治
认真思考一下,发现可以这样递归来搞
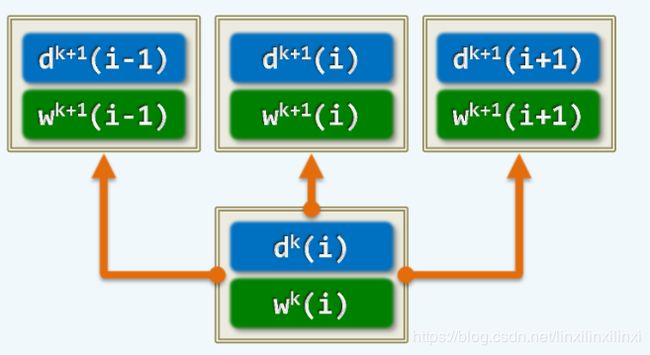
d k ( i ) = w k ( i ) + m i n { d k − 1 ( i − 1 ) , d k − 1 ( i ) , d k − 1 ( i + 1 ) } d^k(i) = w^k(i) + min\{d^{k - 1}(i - 1), d^{k - 1}(i), d^{k - 1}(i + 1)\} dk(i)=wk(i)+min{dk−1(i−1),dk−1(i),dk−1(i+1)}
4.3.1.1 时间复杂度
这样我们看似使用了非常优美的递归来解决问题,但请冷静下来分析一下时间复杂度
这样,我们会惊喜的发现:时间复杂度竟然和刚刚的暴力枚举算法是一样的
问题出现在哪里呢?
问题就出现在,我们重复计算了大量相同的问题,因此浪费了大量的时间
最高层的每一个位置我们只计算了一次,那么第二层平均每个会被上方的三个位置计算 3 3 3次,以此类推,第三层每个位置便会计算 3 2 3^2 32次…
如何解决呢?
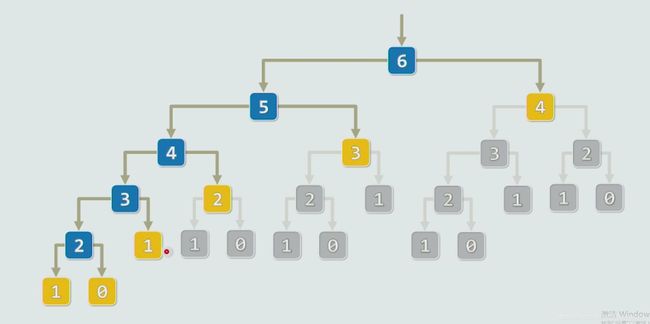
4.3.1.2 记忆化搜索
我们发现,每一个位置的最优情况,只和它的位置有关,而跟他的内部路线与接下来的选择无关,这就是我们所说的无后效性
这样的话,我们可以开一个 n × m n\times m n×m的数组来储存所有位置的最优情况,然后将其初始化为 u n d i f i n e undifine undifine状态
只有当这个位置没有被计算过的时候,我们才需要继续递归分治解决这个子问题,否则的话,直接使用之前计算好并储存下来的结果就好
这样的话每一个位置至多会被计算一次,这时候我们会发现时间复杂度已经降到了 O ( n ∗ m ) O(n*m) O(n∗m)
4.3.2 正儿八经的动态规划
4.3.2.1 记忆化?
刚刚我们为什么需要记忆化呢
回想刚刚的问题,我们之所以需要递归分治并且记忆化的原因是:
我们需要的子问题的答案我们还没有计算出来
我们如何才能行云流水的推进过来,不需要询问没有解决的子问题呢
4.3.2.2 动态规划
我们考虑将刚才的过程颠倒过来
我们从底层往上层走:
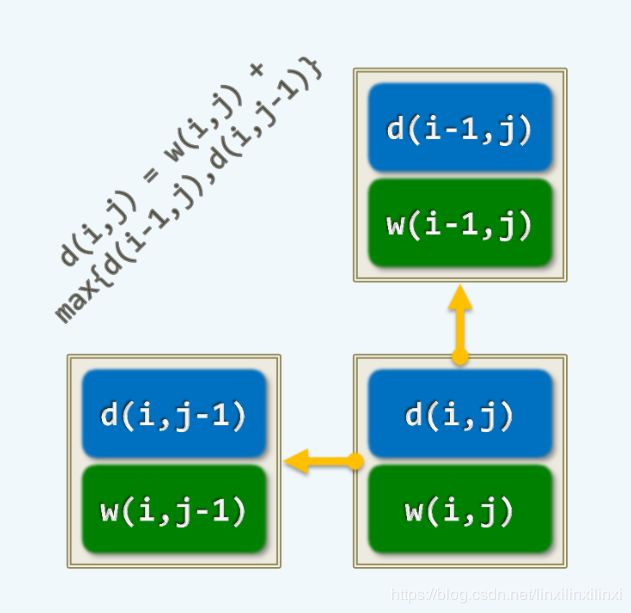
d p [ k ] [ i ] = w [ k ] [ i ] + m i n { d p [ k − 1 ] [ i − 1 ] + d p [ k − 1 ] [ i ] + d p [ k − 1 ] [ i + 1 ] } dp[k][i] = w[k][i] + min\{dp[k - 1][i - 1] + dp[k - 1][i] + dp[k - 1][i + 1]\} dp[k][i]=w[k][i]+min{dp[k−1][i−1]+dp[k−1][i]+dp[k−1][i+1]}
这样从底层往上层推进,我们会惊喜的发现,当我们推进到第 i i i层的时候,第 i − 1 i - 1 i−1层的所有子问题都已经解决并且记录下了
而且我们发现每次只需要上一层的数据,并不需要再之前的所有子问题,我们还可以考虑滚动数组来降低空间复杂度
5 最长曼哈顿路径问题
5.1 问题描述
LMP(Longest Manhattan Path)
在某一个非负整数构成的 n × m n\times m n×m矩阵中,找出从左上角通往右下角的一条路径,使得路径总长(沿途所经整数的总和)最大(你只能在矩阵内部向右走或者向下走)
5.2 问题分析
5.2.1 考虑见神杀神的记忆化搜索
5.2.2 考虑一路高歌猛进的动态规划
不多赘述
6 小结
我们发现,递归分治记忆化与动态规划本质上其实相差不多
而相对来说,记忆化搜索会更加好理解一些,而我们的第一反应也大多是记忆化搜索
递归是从最复杂的问题开始,将其分而治之,直到遇到平凡(Trival)的情况,然后一举攻克
而动态规划则是从最简单的情况开始,一层一层的逐步蚕食掉整个问题
我们如何写出动态规划的算法呢
我们将第一反应的从顶向下的递归算法理解,在实现的时候将其颠倒过来,写出一个从底向上的递推转移式
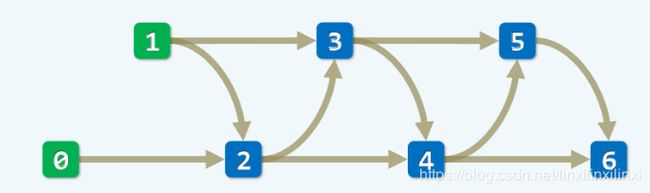
7 最长公共子序列
7.1 问题描述
LCS(Longest Common Subsequnce)
给定两个字符串,问两个字符串的公共子序列中,最长的长度为多少?是哪个?
7.1.1 子串 S u b s t r i n g Substring Substring
原串中连续的一部分
7.1.2 子序列 S u b s e q u n c e Subsequnce Subsequnce
原串中任意抽出任意多个字符(可以不连续,但先后顺序不能变),组成的字符串
7.1.3 举个栗子
在串 N o r t h E a s t N o r m a l U n i v e r s i t y NorthEastNormalUniversity NorthEastNormalUniversity中
E a s t , t N o r , U n i v e r s East, tNor, Univers East,tNor,Univers为其子串
N E N U , o o , t t t , h t l y NENU, oo, ttt, htly NENU,oo,ttt,htly为其子序列
7.2 样例及其分析
7.3 解决问题
7.3.1 相同则减而治之
s 1 [ i ] = = s 2 [ j ] s1[i] == s2[j] s1[i]==s2[j]
7.3.2 不同则分而治之
s 1 [ i ] ! = s 2 [ j ] s1[i] != s2[j] s1[i]!=s2[j]
7.4 转移方程
scanf("%s", a + 1);
scanf("%s", a + 1);
int la = strlen(a + 1);
int lb = strlen(b + 1);
for(int i = 1; i <= la; ++i){
for(int j = 1; j <= lb; ++j){
if(a[i] == b[j]) dp[i][j] = dp[i - 1][j - 1] + 1;
else dp[i][j] = max(dp[i - 1][j], dp[i][j - 1]);
}
}
7.5 dp表
7.6 思考题
如何输出公共最长子序列的内容,以及统计最长公共子序列的个数
(一般来说,寻找长度之类的问题比较容易,追溯解就会比较难搞)
(一般来说,寻找任一最优解比较容易,最优解计数问题比较难搞)
8 背包问题(推荐 背包九讲)
当前你有一个背包,有一系列的物品,物品都有自己的数量、重量 w [ i ] w[i] w[i]以及价值 v [ i ] v[i] v[i],请问在不超过背包总重量 W W W的情况下获得的最大价值是多少(物品不能切分)
考虑贪心:
-
优先选择重量最小的
-
优先选择重量最大的
-
优先选择单位重量价值最高的
都很容易举出反例来
8.1 01背包问题
所有物品的数量都为1
8.1.1 选还是不选,这是一个问题
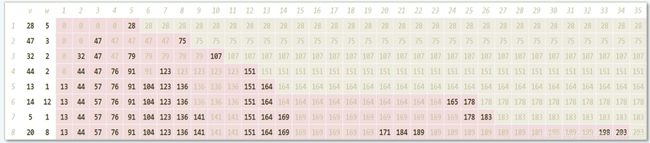
考虑动态规划,用数组 d p [ i ] [ j ] dp[i][j] dp[i][j]表示只考虑前 i i i个物品,背包总承重为 j j j的情况下,能获得的最大价值
8.1.2 分析转移方程
对于每个物品我们都有两种情况
-
选:获得的最大价值为 d p [ i − 1 ] [ j − w [ i ] ] + v [ i ] dp[i - 1][j - w[i]] + v[i] dp[i−1][j−w[i]]+v[i]
-
不选:获得的最大价值为 d p [ i − 1 ] [ j ] dp[i - 1][j] dp[i−1][j]
这样的话,我们便很容易得到转移方程
d p [ i ] [ j ] = { d p [ i − 1 ] [ j ] j < w [ i ] m a x { d p [ i − 1 ] [ j ] , d p [ i − 1 ] [ j − w [ i ] ] + v [ i ] } j > = w [ i ] dp[i][j] = \begin{cases} dp[i - 1][j] & j < w[i] \\ max\{dp[i - 1][j], dp[i - 1][j - w[i]] + v[i]\} & j >= w[i] \end{cases} dp[i][j]={dp[i−1][j]max{dp[i−1][j],dp[i−1][j−w[i]]+v[i]}j<w[i]j>=w[i]
8.1.3 dp表
8.1.4 代码实现
for(int i = 0; i < n; ++i){
for(int j = 0; j < w[i]; ++j){
dp[i][j] = dp[i - 1][j];
}
for(int j = w[i]; j <= W; ++j){
dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - w[i]] + v[i]);
}
}
优化空间
for(int i = 0; i < n; ++i){
for(int j = W; j >= w[i]; --j){
dp[j] = max(dp[j], dp[j - w[i]] + v[i]);
}
}
注意第二层循环顺序为倒序,因为每个物品只有一个,如果正序更新的话会出现当前物品多次选择的情况
8.2 完全背包问题
所有物品的数量都为无限多个
for(int i = 0; i < n; ++i){
for(int j = w[i]; j <= W; ++j){
dp[j] = max(dp[j], dp[j - w[i]] + v[i]);
}
}
8.3 多重背包问题
数量不定
需要考虑二进制优化
9 最长不降子序列LIS
9.1 定义
设有一个正整数序列 a [ n ] : a 1 , a 2 ⋯ , a n a[n]: a_1, a_2 \cdots, a_n a[n]:a1,a2⋯,an对于下标 i 1 < i 2 < ⋯ < i h i_1<i_2 < \cdots<i_h i1<i2<⋯<ih,若有 a i 1 , a i 2 ⋯ a i h a_{i_1}, a_{i_2} \cdots a_{i_h} ai1,ai2⋯aih,
则称序列 a [ n ] a[n] a[n]含有一个长度为 h h h的不下降子序列。
例如,对于序列 3 , 7 , 9 , 16 , 38 , 24 , 27 , 38 , 44 , 49 , 21 , 52 , 63 , 15 3, 7, 9, 16, 38, 24, 27, 38, 44, 49, 21, 52, 63, 15 3,7,9,16,38,24,27,38,44,49,21,52,63,15
对于下标 i 1 = 1 , i 2 = 4 , i 3 = 5 , i 4 = 9 , i 5 = 13 i_1 = 1, i_2 = 4, i_3 = 5, i_4 = 9, i_5 = 13 i1=1,i2=4,i3=5,i4=9,i5=13
满足 13 < 16 < 38 < 44 < 63 13 < 16 < 38 < 44 < 63 13<16<38<44<63
则存在长度为5的不下降子序列。
9.2 问题描述
当给定序列 a 1 , a 2 ⋯ a n a_1, a_2 \cdots a_n a1,a2⋯an后,请求出最长的不下降序列的长度
9.3 解决问题
9.3.1 O ( n 2 ) O(n^2) O(n2)的算法
对于任意的 i i i, 定义 d p [ i ] dp[i] dp[i]是以 a i a_i ai结束的最长不下降子序列的长度,那么显然,问题的解为 d p [ n ] dp[n] dp[n]。
不妨假设,已求得以 a 1 , a 2 , ⋯ , a j − 1 a_1,a_2, \cdots, a_{j − 1} a1,a2,⋯,aj−1结束的最长不下降子序列的长度分别为 d p [ 1 ] , d p [ 2 ] , . . . , d p [ j − 1 ] dp[1],dp[2],...,dp[j−1] dp[1],dp[2],...,dp[j−1]
其中 d p [ 1 ] = 1 dp[1]=1 dp[1]=1
那么对于 a i a_i ai,其中 i < j − 1 i < j − 1 i<j−1, 若 a i ≤ a j a_i \le a_j ai≤aj,则以 a j a_j aj结束的不下降子序列长度为的 d p [ i ] + 1 dp[i] + 1 dp[i]+1
显然以 a j a_j aj结束的最长不下降子序列的长度
d p [ j ] = m a x { d p [ i ] } + 1 dp[j] = max\{dp[i]\} + 1 dp[j]=max{dp[i]}+1
其中 1 ≤ i ≤ j − 1 , a i ≤ a j 1 \le i \le j − 1, a_i \le a_j 1≤i≤j−1,ai≤aj
更新公式中每次都得从头遍历整个 d p [ i ] dp[i] dp[i],所以算法复杂度为 O ( n 2 ) O(n^2) O(n2)
9.3.2 O ( n l o g n ) O(nlogn) O(nlogn)算法
O ( n l o g n ) O(nlogn) O(nlogn)的算法关键是它建立了一个数组 b [ ] b[] b[]
b [ i ] b[i] b[i]表示长度为 i i i的不下降序列中结尾元素的最小值
用 k k k表示数组目前的长度
算法完成后 k k k的值即为最长不下降子序列的长度。
不妨假设,当前已求出的长度为 k k k
则判断 a [ i ] a[i] a[i]和 b [ k ] b[k] b[k]:
如果 b [ k ] ≤ a [ i ] b[k]\le a[i] b[k]≤a[i],即 a [ i ] a[i] a[i]大于长度为 k k k的序列中的最后一个元素
这样就可以使序列的长度增加 1 1 1,即 k = k + 1 k = k + 1 k=k+1 然后更新 b [ k ] = a [ i ] b[k] = a[i] b[k]=a[i];
如果 b [ k ] > a [ i ] b[k] \gt a[i] b[k]>a[i]
那么就在 b [ 1 ] ⋯ b [ k ] b[1]\cdots b[k] b[1]⋯b[k]中找到最大的 j j j使得 b [ j ] < a [ i ] b[j] < a[i] b[j]<a[i],即 a [ i ] a[i] a[i]大于长度为 j j j的序列的最后一个元素
显然, b [ j + 1 ] ≥ a [ i ] b[j+1] \ge a[i] b[j+1]≥a[i], 那么就可以更新长度为 j + 1 j + 1 j+1的序列的最后一个元素,即 b [ j + 1 ] = a [ i ] b[j + 1] = a[i] b[j+1]=a[i]。
可以注意到: b [ i ] b[i] b[i]单调递增,很容易理解,长度更长了, d [ k ] d[k] d[k]的值是不会减小的,因此更新公式可以用二分查找,所以算法复杂度为 O ( n l o g n ) O(nlogn) O(nlogn)。
代码实现
const int maxn = 5e4 + 10;
int a[maxn], b[maxn];
//用二分查找的方法找到一个位置,使得x>b[i - 1],并且x
int src(int x, int l, int r){
while(l <= r){
int mid = (l + r)/2;
if(x >= b[mid]) l = mid + 1;
else r = mid - 1;
}
return l;
}
int dp(int n){
b[1] = a[1];
int len = 1;
for(int i = 2; i <= n; ++i){
if(a[i] >= b[len]) b[++len] = a[i]; //如果a[i]比b数组中最大的数还大,便将此数直接插入到b数组后面
else b[src(a[i], 1, len)] = a[i]; //二分查找第一个比a[i]大的位置并且让a[i]代替这个位置
}
return len;
}