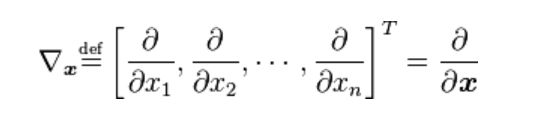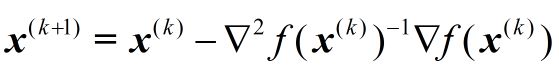数学优化入门:梯度下降法、牛顿法、共轭梯度法
1、基本概念
1.1 方向导数
1.2 梯度的概念

因此,对于一元函数,即y=f(x),其梯度的方向总是指向x轴正方向或反方向,而大小即该点的导数。
如果考虑z=f(x,y)描绘的是一座在点(x,y)的高度为f(x,y)的山。那么,某一点的梯度方向是在该点坡度最陡的方向,而梯度的大小告诉我们坡度到底有多陡。
1.3 梯度与方向导数
函数在某点的梯度是这样一个向量,它的方向与取得最大方向导数的方向一致,而它的模为方向导数的最大值。
1.4 梯度与等高线
函数z=f(x)在点P(x,y)的梯度的方向与过点的等高线f(x,y)=c在这点的法线的一个方向相同,且从数值较低的等高线指向数值较高的等高线,而梯度的模等于函数在这个法线方向的方向导数。这个法线方向就是方向导数取得最大值的方向。
即负梯度方向为最速下降方向。
1.5 等高面
对于二次函数
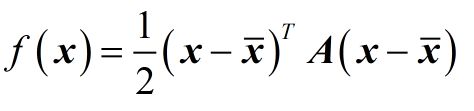
其中A为n*n的对称正定矩阵,x-为一定点,则函数f(x)的等值面f(x,y)=c是一个以x-为中心的椭球面。
此椭球面的形状受 Hesse 矩阵的条件数影响,长轴与短轴对应矩阵的最小特征值和最大特征值的方向,其大小与特征值的平方根成反比,最大特征值与最小特征值相差越大,椭球面越扁。
矩阵的条件数:矩阵A的条件数等于A的范数与A的逆的范数的乘积,即cond(A)=‖A‖·‖A^(-1)‖,是用来判断矩阵病态与否的一种度量,条件数越大矩阵越病态。
1.6 Hesse 矩阵
1.7 Jacobi矩阵
前面讲的都是从n维空间到一维空间的映射函数,对于从n维欧式空间变换到m维欧式空间的函数f,也可以表示成由m个实函数组成y=f(x)=[y1(x1,…xn),…ym(x1,…,xn)]T。对于函数f,如果其偏导数都存在,可以组成一个m行n列的矩阵,即所谓的Jacobi矩阵:
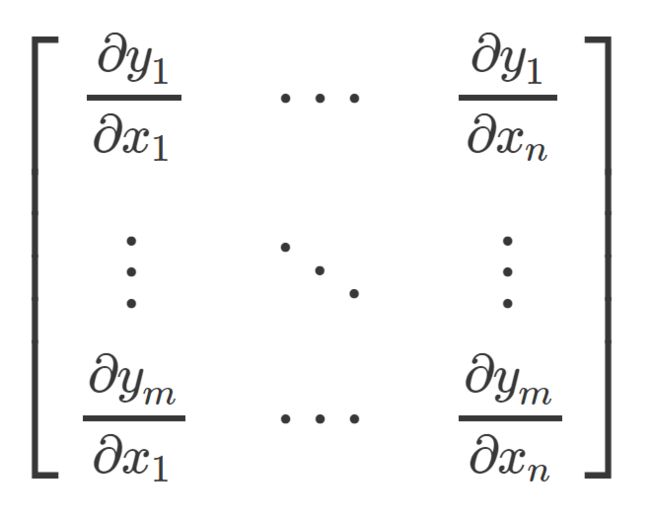
显然, 当f(x) 是一个标量函数时,Jacobi矩阵是一个向量,即f(x)的梯度,此时Hesse 矩阵是一个二维矩阵;当f(x)是一个向量值函数时,Jacobi 矩阵是一个二维矩阵,Hesse 矩阵是一个三维矩阵。
1.8 共轭方向
当A为单位阵时,这两个方向关于A共轭将等价于两个方向正交,可见共轭是正交概念的推广。
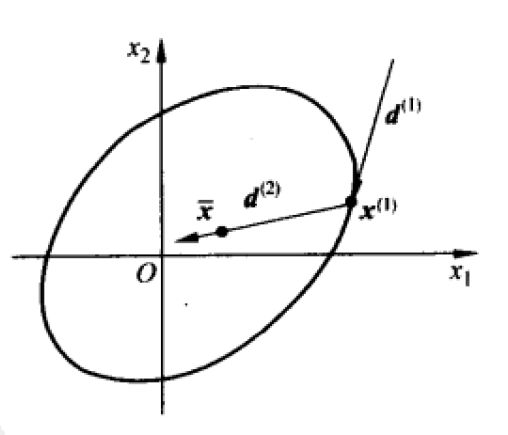
我们在来看共轭方向的几何意义。
前面提到过二次函数
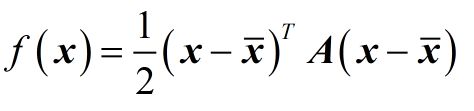
的等值面f(x,y)=c是一个以x-为中心的椭球面。设x^(1)为此椭球面边缘的一点,则x^(1)处的法向量为

将其中后面一项记作
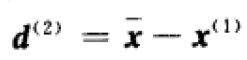
即由x(1)指向椭圆面中心x-的向量。
下面,设d^(1)为此椭球面在x(1)处的切向量,由于切向量d^(1)与法向量delta f(x(1))正交,即

可见,等值面上一点处的切向量与由此点指向极小点的向量是关于A共轭的。
因此,极小化上述二次函数,若依次沿着d^(1)和d^(2)进行一维搜索,则经过两次迭代必达到极小点。
1.9 一维搜索
在许多迭代下降算法中,具有一个共同点,就是得到x(k)后,按某种规则确定一个方向d(k),再从x(k)除法,沿方向d(k)在直线上求目标函数f(x(k)+lambda*d(k))的的极小点,从而得到x(k)的后继点x(k+1),这里求目标函数在直线上的极小点,称为一维搜索,或者线搜索,可以归结为单变量lambda的极小化问题。确定的lambda可以成为步长。
一维搜索方法很多,大致可以分为试探法和函数逼近法(插值法)。当然,这两种方法都是求得即小的的近似值。
试探法包括0.618法、Fibonacci法、进退法、平分法等。
函数逼近法包括牛顿法、割线法、抛物线法、三次插值法、有理插值法等。
2、梯度下降法(最速下降法)
即利用一阶的梯度信息找到函数局部最优解的一种方法。核心迭代公式为
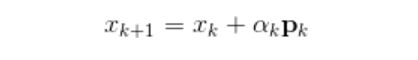
其中,pk是第k次迭代时选取的移动方向,在梯度下降法中,移动的方向设定为梯度的负方向。
ak是第k次迭代是移动的步长,每次移动的步长可以固定也可以改变。在数学上,步长可以通过line search令导数为零找到该方向上的最小值,但是在实际编程时,这样计算的代价太大,我们一般可以将它设定位一个常量。
如果目标函数是一个凸优化问题,那么梯度下降法获得的局部最优解就是全局最优解,理想的优化效果如下图,值得注意一点的是,每一次迭代的移动方向都与出发点的等高线垂直:
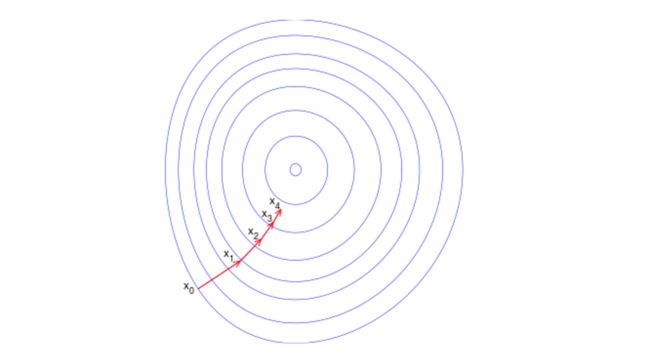
实际上,梯度还可以提供不在最快变化方向的其他方向上坡度的变化速度,即在二维情况下,按照梯度方向倾斜的圆在平面上投影成一个椭圆。椭球面的形状受 Hesse 矩阵的条件数影响,椭球面越扁,那么优化路径需要走很大的弯路,计算效率很低。这就是常说的锯齿现象( zig-zagging),将会导致收算法敛速度变慢。
3、牛顿法
前面提到的梯度下降法,主要利用的是目标函数的局部性质,具有一定的“盲目性”。
牛顿法则是利用局部的一阶和二阶偏导信息,去推测整个目标函数的形状,进而可以求得近似函数的全局最小值,然后将当前的最小值设定为近似函数的最小值。也就是说,牛顿法在二阶导数的作用下,从函数的凸性出发,直接搜索怎样到达极值点,即在选择方向时,不仅考虑当前坡度是否够大,还会考虑走了一步之后,坡度是否会变得更大。
相比最速下降法,牛顿法带有一定对全局的预测性,收敛性质也更优良。当然由于牛顿法是二阶收敛的,比梯度下降法收敛的更快。
显然这里x是自变量,x^(k)是常量,求解近似函数phi(x)的极值,即令其倒数为0,很容易得到
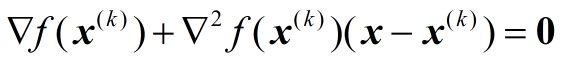
显然除了f(x)二次可微外,还要求f(x)的Hesse矩阵可逆。此外,由于矩阵取逆的计算复杂为 n 的立方,当问题规模比较大时,计算量很大,解决的办法是采用拟牛顿法,如 BFGS, L-BFGS, DFP, Broyden’s Algorithm 进行近似。
此外,如果初始值离局部极小值太远,泰勒展开并不能对原函数进行良好的近似,导致牛顿法可能不收敛。
我们给出阻尼牛顿法的计算步骤,其实阻尼牛顿法相较原始牛顿法只是增加了沿牛顿方向的一维搜索:

4、共轭梯度法
共轭梯度法是介于最速下降法与牛顿法之间的一个方法,它仅需一阶导数信息,但克服了最速下降法收敛慢的缺点,又避免了牛顿法需要存储和计算Hesse矩阵并求逆的缺点。
共轭梯度法的基本思想是把共轭性与最速下降法相结合,利用已知点处的梯度构造一组共轭方向,并沿这组方向进行搜索,求出目标函数的极小点。根据共轭方向的基本性质,这种方法具有二次终止性。
共轭梯度法中的核心迭代过程可以采取不同的方案,一种是直接延续,即总是用d^(k+1)=-g(k+1)+beta_k*d^(k)构造搜索方向;一种是把n步作为一轮,每搜索一轮之后,取一次最速下降方向,开始下一轮,此种策略称为“重置”。
下面我们介绍一种传统的共轭梯度法
注意,上述算法中均假设采用的精确一维搜索,但实际计算中,精确一维搜索会带来一定困难,代价较大,通常还是采用不精确的一维搜索。但此时(4)中构造的搜索方向可能就不是下降方向了,解决这个问题有两个方法。
其一,当d^(k+1)不是下降方向时,以最速下降方向重新开始。事实上,这也存在问题,但一维搜索比较粗糙时,这样重新开始可能是大量的,会降低计算效率。
其二,在计算过程中增加附加的检验,具体细节可以参考陈宝林老师的“最优化理论与方法”的P301。