word2vec以及GloVe总结

词向量

词向量，顾名思义，就是把一个单词或词语表示成一个向量的形式，这是因为在计算机中无法直接处理自然语言，需要把它转化为机器能够理解的语言，比如数值等。最简单的方式是把一个个单词表示成one-hot的形式。例如有三个句子：

我/喜欢/小狗/喜欢/喝咖啡
我/不喜欢/喝咖啡
你/喜欢/什么/东西

词汇表为:

我、你、喜欢、不喜欢、小狗、喝咖啡、什么、东西

然后对每一个词做one-hot编码：
“我”就是[1,0,0,0,0,0,0,0]
“你”就是[0,1,0,0,0,0,0,0]
等等。
则对于每一个句子的表示为：

我	你	喜欢	不喜欢	小狗	喝咖啡	什么	东西
1	0	2	0	1	1	0	0
1	0	0	1	0	1	0	0
0	1	1	0	0	0	1	1

这样对各个词做成了词向量，但这种缺点是稀疏性大，如果词汇集很多则每一个词的维度非常大，会造成维度灾难。不过经近几年的发展，词向量可以表示成密集向量（dense vector），并且可以使用较少的维度表示一个词，其称之为word embedding或Distributed representation。这就是下面将要说的word2vec和GloVe模型。在介绍它们两个之前，先说一说神经网络语言模型（NNLM）。

神经网络语言模型（NNLM）

NNLM由Bengio等人提出，他的主要想法就是：
1. 把字典里的每一个单词对应一个词特征向量
2. 把单词序列表示成联合概率函数
3. 自动学习词特征向量和概率函数的参数
在NNLM中，每一个单词为向量空间中的一个点，而且特征的数目要比字典的大小要小，它的概率函数表示为在给定前一个词下，后一个词的条件概率的乘积。

模型结构

假设训练集为 w1,...,wT 的单词序列，单词 wt∈V ， V 是大量且有限的词汇集。目标是学习一个模型 f(wt,...,wt−n+1)=P^(wt|wt−11) ， wt−11 为单词从 w1到wt−1 。对于任意的 wt−11 ，模型的唯一约束为 Σ|V|i=1f(i,wt−1,...,wt−n+1)=1,f>0 。
在这个神经网络模型中，它把这个概率函数分为两部分走：
1. 一个映射 C ，即可以把 V 中任意一个词 i 映射为一个实值向量 C(i)∈Rm ，它表示的就是单词 i 的分布式特征向量（distributed feature vector）。在实践中， C 被表示成一个 |V|×m 的矩阵，即矩阵的每一行 C(i) 代表一个词的词向量。他们也即模型的输入。
2. 单词的概率函数。通过一个函数 g 把输入的上下文单词的特征向量 (C(wt−n+1),...,C(wt−1)) 映射为下一个单词 wt 的条件概率分布函数，当然，这个单词 wt 在字典 V 中。 g 输出的的向量的第 i 个元素就是第 i 个单词的条件概率：

f(i,wt,...,wt−n+1)=g(i,C(wt−n+1),...,C(wt−1))

现在再来看下面这一张图就明白了：

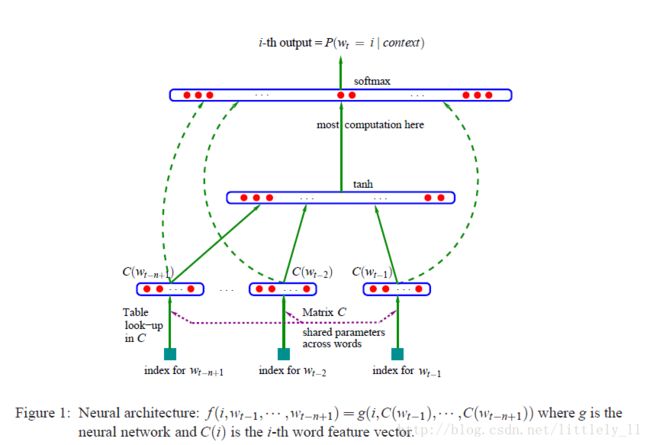
首先是对整个词汇表建立一个索引，每个单词对应一个索引号，其实就是one-hot编码，然后把要抽取单词的这些one-hot编码建立索引矩阵 D ，维度为 (n−1)×|V| ，即每一行代表一个单词的one hot representation。而矩阵 C 每一行为一个单词的词向量，这样 D⋅C 就抽取出对应单词的向量了，这就是图中的table look-up in C ，找出对应的词向量后，将这些词向量拼接在一起，形成一个 (n−1)m 维的列向量 x ，经过隐含层tanh函数的激活，再经过softmax输出层的输出，这就得到了函数 g 的输出向量。需要注意的一点是：在输入层到输出层有直接相连的，这一层连接是可选的，下面讲述的没有考虑这一情况。
目标函数的训练是最大化对数似然函数：

L=1TΣtlogf(wt,wt−1,...,wt−n+1;θ)+R(θ)

其中， θ 为待训练参数， R(θ) 为正则化项。而正则化项只约束于网络的权重和矩阵 C ，并不约束于偏置项。
最终输出的 y 为：

y=b+Wx+Utanh(d+Hx)

这个 y 就是一个 |V| 维的列向量。
假设 h 为隐藏单元个数， m 为每个单词的特征数，也即维度，矩阵 W 维度为 |V|×(n−1)m ，可设置为0， x 为拼接的列向量，维度为 (n−1)m ，偏置 b 维度为 |V| ，隐藏层中的偏置 d 维度为 h ，隐藏层到输出层的权重 U 维度为 |V|×h ，输入至隐藏层权重 H 维度为 h×(n−1)m ，则：

θ=(v,d,W,U,H,C)

参数个数为 |V|(1+nm+h)+h(1+(n−1)m) ，起决定性的为 |V|(nm+h) 。
在训练的时候可以使用随机梯度上升法：

θ←θ+ϵ∂logP^(wt|wt−1,...,wt−n+1)∂θ

这就是完整的神经网络语言模型（NNLM）结构。

word2vec模型

Mikolov（2013）等人提出了一个新型的模型结构——word2vec模型，此模型的优点为能训练大量的语料，可以达到上亿的单词，并且可以使单词向量维度较低，在50-100之间。它能够捕捉单词之间的相似性，对单词使用代数运算就能计算相似的单词，例如：vector(“King”)-vector(“Man”)+vector(“Woman”)=vector(“Queen”)，挺厉害吧。其实还有其他模型可以计算词向量，如隐含语义分析（Latent Semantic Analysis,LSA），Latent Dirichlet Allocation(LDA)等，但Word2vec比他们两个要好。

word2vec模型结构

word2vec模型有两种方法来实现，一个是基于CBOW（continuous bag of word），另一个是基于skip-gram模型。这两种结构如下图：

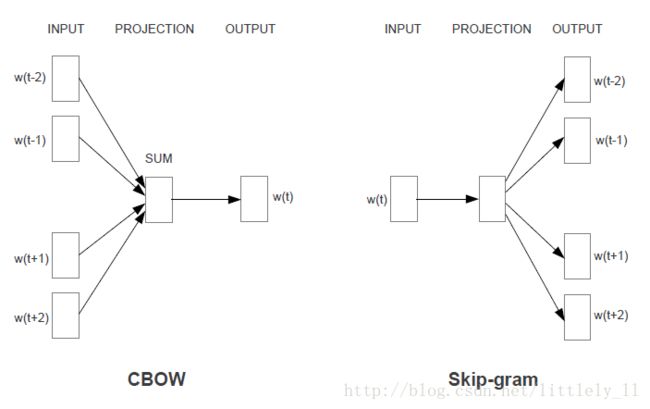
基于CBOW模型是根据目标单词的上下文经过映射来预测目标单词，而基于skip-gram模型刚好相反，使用目标单词经过映射层来预测上下文单词。
而这两个模型又可以使用两种方法实现，即使用hierachical softmax和negtive sampling来实现。

基于Hierachical softmax的CBOW和skip-gram模型

基于hierachical softmax的CBOW模型的目标函数是：

L=Σw∈VlogP(w|Context(w))

而基于hierachical softmax的skip-gram模型目标函数为：

L=Σw∈VlogP(Context(w)|w)

CBOW模型的结构层次为三层：
1. 第一层为输入层，即单词 w 的上下文 Context(w) ;
2. 中间为映射层，即把输入层的词向量加在一起；
3. 最后为输出层，是一个Huffman树
和NNLM比较，NNLM有一个隐含层，而CBOW变为映射层；NNLM把输入的词向量拼接在一起，而CBOW是加在一起，NNLM输出为使用softmax，而CBOW输出的是一颗Huffman树。在NNLM中，最大的复杂度体现在隐藏层，而在隐藏层到输出层又是计算密集的，所以CBOW更改了这两层以提高效率。
skip-gram模型层次与CBOW模型一样，主要区别就是映射层可有可无，因为目标词 w 在映射层的加和仍然是它本身。

基于Negtive sampling的CBOW和skip-gram模型

negtive sampling是一种采样方法，假设一个目标单词 w 与它的上下文单词为 Context(w) ，这属于一个正例，而负采样就是在词汇表中抽取n个 与 w 不同的词 wi,i=1,2,...,n ，这些个 wi 与 Context(w) 就组成了负样本，然后对这个正例和这些负例进行二元逻辑回归得到 wi 的参数及其词向量。因此nagtive sampling与hierachical softmax的主要不同就是在输出层上没有使用Huffman树，而是使用负采样。

CBOW和Skip-gram模型的推导

对于CBOW和skip-gram模型以及它们实现的两种方法Hierachical softmax和negtive sampling的具体推导可以参见：
word2vec原理(一) CBOW与Skip-Gram模型基础
word2vec 中的数学原理详解（一）目录和前言
他们讲的非常好，推导非常详细，很值得一看。

对于word2vec模型的实现，有python的库gensim及Google的C代码。

GloVe模型

在word2vec模型提出不久，Jeffrey Pennington等人认为虽然skip-gram模型在计算近义词方面比较出色，但它们只是在局部上下文窗口训练模型，并且它很少使用语料中的一些统计信息，因此Jeffrey Pennington等人又提出了一个新型模型GloVe。
首先给一些说明，词-词共现计数矩阵可以表示为 X ，则 Xij 为单词 j 出在单词 i 上下文中的次数。 Xi=ΣkXik 表示任何词出现在单词 i 上下文中的次数， Pij=P(j|i)=XijXi 表示单词 j 出现在单词 i 上下文中的比率。
使用一个例子来说明是怎样从共现概率中抽取确定的意思，其实也就是说，和哪个上下文单词在一起的多，那么这个单词与这个上下文单词在一起要比与其他词在一起意义要大。例如i=ice, j=steam，假设有共现词k，但是k与ice的联系要比与steam的联系强，也就是说单词k与ice出现的概率比与’steam’出现的概率大，比如说k=solid，那么我们认为 Pik/Pjk 会很大。相似地，如果单词k与steam的联系比与ice的联系强，例如k=gas，那么 Pik/Pjk 的比率会很小，对于其他的单词k如water, fashion与ice,steam联系都强或都不强的话，则 Pik/Pjk 的比率会接近1。那么这个比率就能区别相关词（solid, gas）和不相关词（water, fashion），并且也能区别这两个相关的词（solid, gas）。那么得到的向量可能为ice-steam=solid-gas，这与word2vec相似。
但是要训练的目标函数是什么呢？

GloVe模型推导

对于词向量的学习开始于共现概率的比率 Pik/Pjk 而不是而不是原始概率 Pik，Pjk ，比率 Pik/Pjk 依赖三个单词 i,j,k ，则最一般的模型形式为：

F(wi,wj,w~k)=PikPjk

其中， w∈Rd 是词向量， w~∈Rd 是上下文单词向量。
由于向量空间是线性的，所以可以把两个向量表示为向量的差，则可以把上式写成：

F(wi−wj,w~k)=PikPjk

由于等式右边是一个标量，则等式左边参数可以表示为点积形式：

F((wi−wj)Tw~k)=PikPjk

由于一个单词与其上下文单词的区别是任意的，它们两个的角色是可以互换的，所以单词 w 与 w~ 可以互换，并且矩阵 X 与 XT 也是可以互换的，但对于最终结果是不变的。
然后把原始概率用 F 函数表示，则：

F((wi−wj)Tw~k)=F(wTiw~k)F(wTjw~k)

其中， F(wTiw~k)=Pik=XikXi 。当 F=exp 时，上式为：

wTiw~k=log(Pik)=log(Xik)−log(Xi)

因为多存在了一个 log(Xi) ，所以这个式子不具有对称性，我们注意到， log(Xi) 与k无关，所以把这一项放到了对 wi 偏置的 bi 中，最后再加上对 w~k 的偏置 b~k ，则：

wTiw~k+bi+b~k=log(Xik)

此式是 F(wi,wj,w~k)=PikPjk 的简化，并具有对称性。注意一点，当 Xik 接近于0时对数是发散的，所以可以把 log(Xik) 转化为 log(1+Xik) 。
该模型的一个主要缺点为它认为所有的共现词权重相等，即使很少出现或没有出现的词，所以为了克服这一缺点，使用了加权最小二乘回归模型：

J=ΣVi,j=1f(Xij)(wTiw~j+bi+b~j−log(Xij))2

其中， f(Xij) 为权重函数， V 为词汇量。
权重函数有以下属性：
1. f(0)=0
2. f(x) 为非递减函数
3. 对于大的 x ， f(x) 应相对较小。
Jeffrey Pennington等人给出了一个 f(x) 函数：

f(x)={(x/xmax)αifx<xmax1otherwise

α 的经验取值为3/4。

不同模型的对比

Omer Levy等人对基于计数的方法和基于embedding的方法做了对比，发现它们之间并没有非常大的差距，在不同的场景各个模型发挥不同的作用，它们之间并没有谁一定优于谁，相比于算法而言，增加语料量，进行预处理以及超参数的调整显得非常重要。特别指出，基于negtive sampling的skip-gram模型可以作为一个基准，尽管对不同的任务它可能不是最好的，但是它训练快，占用内存和磁盘空间少。



参考文献
【Yoshua Bengio, Réjean Ducharme,Pascal Vincent , Christian Jauvin】A Neural Probabilistic Language Model
【Tomas Mikolov, Kai Chen, Greg Corrado, Jeffrey Dean】Efficient Estimation of Word Representations in Vector Space
【Tomas Mikolov, Ilya Sutskever, Kai Chen, Greg Corrado, Jeffrey Dean】Distributed Representations ofWords and Phrases and their Compositionality
【Jeffrey Pennington, Richard Socher, Christopher D. Manning】GloVe: Global Vectors forWord Representation
【Omer Levy, Yoav Goldberg, Ido Dagan】Improving Distributional Similarity with Lessons Learned from Word Embeddings