PCA算法及其应用（代码）

简介

PCA（Principal Component Analysis）算法叫做主成分分析，在进行图像识别以及高维度数据降维处理中有很强的应用性，算法主要通过计算特征值最大的特征向量来对原始数据进行线性变换。
本文将从算法原理角度来分析PCA算法的可行性，文中将引入人脸识别的概念，从而介绍PCA在人脸识别1中的应用。本文将包含以下内容：

1. 从向量空间角度来直观理解PCA算法
2. PCA算法的具体步骤以及其中包含的小技巧
3. PCA算法的实际应用及其部分代码和运行结果

文章中的代码以matlab为准，对于PCA的理解可能不具有较强数学严谨性，因为我习惯从直观（intuitive）的角度来理解这些算法。下面进入正文。

PCA算法理解

这一小节将引入人脸识别概念，再加上数学中线性代数的知识从而直观理解PCA算法。本文尽量简化数学概念，但还是需要读者有部分线性代数的知识，之后可能会另开一博文介绍向量空间（space）、子空间（subspace）和线性变换（linear transformation）等的概念，有兴趣可以学习可汗学院的线性代数公开课2。在介绍原理时，我尽量保证直观易懂。

人脸图像的识别

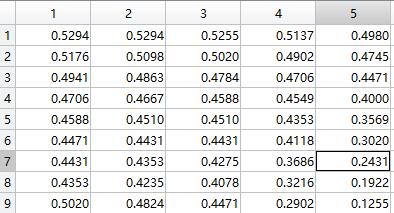
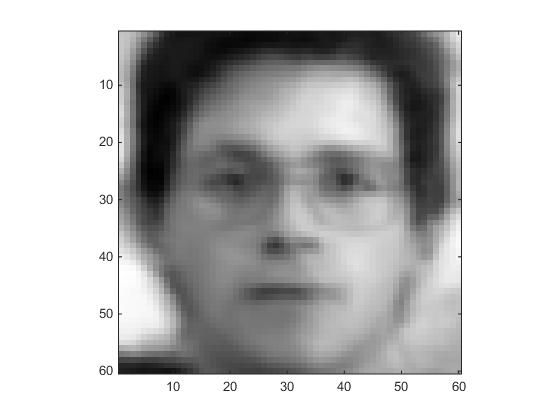
在进行人脸图像识别时，如果给我们一组正面对着我们的灰度人脸图片，每张图片大小一样，因为图片在存储时也就是一个像素点一个数，图片也就是一个矩阵。把这个矩阵都按照列首位相连组成一个向量，我们就可以得到一组人脸向量。那么接下来的叙述中，人脸矩阵就等于人脸向量，只不过一个是二维上的图片便于展示，另一个是一维上的数学便于运算。如图（1）左是一个人脸，而数据其实就是右边这样的矩阵，越接近1越白，越接近0越黑。

图1

因为这些人脸都是正面对着我们，最多有光照不同（比如同一张脸在侧面光照和正面光照时的人脸向量是不同的），所以脸都差不多，不会出现很奇怪的三角形，梯形的脸这种情况。所以，这些脸向量虽然看起来好像是每个向量的元素都可能有任意的（0-1）的任何数值，但其实这些数值之间是相关的。也就是说，人脸向量的各个元素之间其实是有关联的，不可能是相互独立出现的，那样就不能称之为人脸了（梵高的画里的人脸倒是可以任意的）。

这样看来，其实人脸并不是一个向量的完整空间，而是一个向量空间的子空间（subspace），什么叫子空间，又如何理解这样的子空间呢？

向量空间及子空间简介

这一节的知识是线性代数里面的知识，我会介绍线性空间、线性变换以及子空间的概念。需要有大一上过的线性代数（高等代数）知识作为基础，内容只做简单介绍，之后可能会开另一博文来详细介绍这部分的数学知识。如果不是很感兴趣，可以直接跳过该节，也不太影响对PCA的理解。

线性空间与线性变化

在二维坐标下，任意一个向量可以表示成两个基向量（basis）的和，所以坐标其实只是两个基向量之前的系数而已。例如，坐标 (3,4)T 其实可以表示成

[34]=3∗[10]+4∗[01]

的形式，所以虽然写的是 (3,4)T 但是我们默认是这两个标准基向量(standard basis)前的系数，这也是一个正交坐标系的表示。如果我们的基向量不是这样的呢？我们发现任意两个 线性无关（linearly independent）的向量都可以构成二维坐标下的一组基向量。所以我们可以通过某种变换来将某个坐标系变成另一个坐标系，也就是基向量改变了。这个二维坐标系就是一个二维空间（space），两个标准基向量就称为该坐标系下面的一组基。
一个向量可以用该空间下的一组基通过线性组合表示。这时候，线性组合的系数就称为坐标（coordinate）。
一个空间下，我们往往可以找到很多组基，这就说明对同一个向量，可以有不同的表示方法。同一向量在不同基下的坐标也不同，但是之间是存在某种关系的，比如 W=(w1,w2,...,wn) 是一组基向量，而 V=(v1,v2,...,vn) 是另一组基。一个向量 x 在 W 组合下表示成 [x]w ，在 V 组合下表示成 [x]v ，那么我们有

[x]w=(W−1V)[x]v(1)

这就是线性变换（linear transformation），其中的 W−1V 叫做变换矩阵（transition matrix）。（看到这里，估计大家都有点累了，还剩一点点知识咱们就能回到PCA上面来了）

子空间

我们在线性代数中学过，一个 n 维向量空间必须要有 n 个线性无关的基才能完整表示，如果我们只有少于 n 个基向量怎么办呢？这里可以直观上理解成，这 (n−k) 个基将构成一个子空间，因为它不能表示 n 维空间中的全部向量，只有部分能够表示出来。但是有时候，往往我们需要的就只是那部分，那些不能表示的部分可能是一些不仅对结果没有影响反而可能让结果变差的部分，所以如果我们只研究子空间，说不定会看到更好的结果。
打个比方，我们的整个空间是一片沙漠，我们关心的是这个沙漠中哪里有绿洲。如果你用一些数字来表示整个沙漠，那需要很高的精度的数字，有时候一点点噪声就会让我们很难找到这个绿洲。但把范围缩小，我们假设绿洲只会出现在曾经出现过绿洲的区域，只需要很小的精度就可以把这些区域都定位清楚了。
对子空间的介绍，我们采用的是很形象化的理解，没有数学上严格的证明。数学上证明可以参考维基百科。一句话总结子空间，子空间是空间的一部分，可以用空间的部分基向量表示。

PCA与人脸识别

上面介绍了人脸其实是非常相似的，也就是说虽然一个人脸向量可能是36003维的，但是其实这些人脸向量是3600维空间中的一个子空间的向量。所以，我们没有必要用3600个基向量来组成这个人脸向量，只要找到这个子空间所需要用的基向量就可以了。
那么我们怎么知道那些是子空间的基向量呢？那些组成数据点的基向量，肯定是对这个数据点改变很大的基向量，如果加上某个基向量和不加这个基向量，对数据点不会产生什么影响，那么这个基向量就不是一个重要的基向量，我们就不用考虑它了。讲起来很绕，举个例子吧，如果我们有一组二维数据如

图2
所示。我们假设这个二维空间存在一个一维子空间，只有一个基向量就可以表示，我们怎么确定这个基向量是多少呢？其实直观上，就是把这些数据点投影到哪个向量上面会更好。如果投影到x轴，或者y轴就是选了坐标点，我们发现不是很理想，因为会让有的数据点太接近了不好区分，于是我们考虑如下的向量投影方式
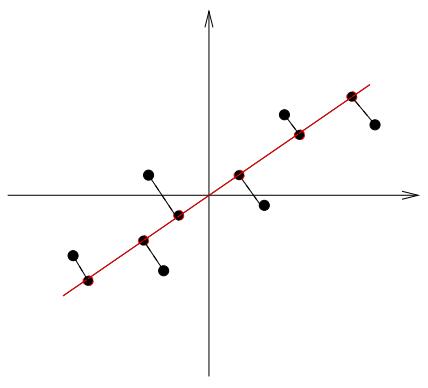
图3
就可以比较好的将这些数据区别开了，举个更清楚的例子，如果采用另外一个基向量表示，如
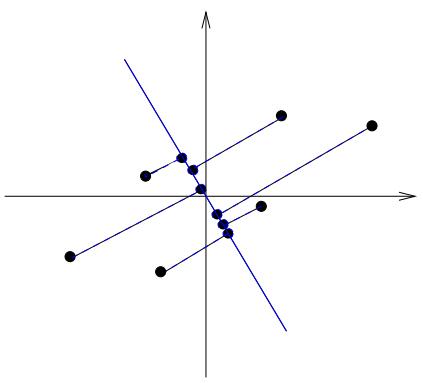
图4
就很难区别这些数据点了，说明这个基向量不是一个好的基向量：）。
也就是说我们希望找到的基向量，能够使这些点之间差距更大，更容易区别开。将上述例子用更数学的语言来描述，我们希望
找到一组基向量来线性表示这些人脸向量，得到新的坐标向量能够有最大的方差。

PCA算法步骤

PCA做的事情就是找到这样一组基向量来表示已有的数据点，不仅仅是将高维度数据变成低维度数据，更能够找到最关键信息。将上节说的找到最大的方差这种表述，用数学符号表示，假设已有数据 {xi},i=1,2,...,n ，希望能够找到一组基向量使得这些数据向量在基向量上的分量（长度，投影）最大。定义在基向量 wi 上投影分量大小为 yi ，可以得到

yi=wi⋅(xi−m)(2)

其中m是数据点的中心，也就是说

m=1n∑i=1nxi(3)

这样计算。
我们要解决这样的一个问题：对 i=1,2,...,n ，找到长度为1的基向量 wi ，使得 yi 的方差最大（即最好区分），形式化为

argmaxwiVar(yi)，s.t.||wi||=1(4)

，其中 Var(yi) 按照

Var(yi)=E[(y−E(y)2](5)

计算， E(⋅) 表示数学期望。
上述方程的求解将用到拉格朗日数乘法（lagrange Multipliers），我会另开一博文一步步介绍如何求解。可以得到解为

Cwi=λwi,||wi||=1.(6)

其中 C 是 Z=(X−m) 的协方差矩阵(covariance matrix)，

C=E{(X−m)(X−m)T}(7)

可以发现 wi 其实就是所要求的特征向量。于是我们的问题，就变成了，求 Z 的协方差矩阵 C ，然后求出 C 的特征向量，这些就是要找的基向量。下面将按步骤叙述PCA算法：

---

1. 按照式(3)计算样本均值 m ；
2. 按照式(7)计算协方差矩阵 C ；
3. 求出 C 的特征向量及对应的特征值并归一化，特征值的大小对应该特征向量的重要性；（补充一下，按照定理，因为协方差矩阵式对称的，所以特征值一定是正的）
4. 选前K个特征向量（按特征值大小排序），这就是我们要找的基向量；
5. 将基向量作为矩阵的列构成一个新的矩阵 V ；
6. 每个数据点的主成分 ci （变换后的坐标）计算为:
   
   ci=VTzi(8)

---

通过以上步骤，我们就完成了PCA算法的全部内容，将数据点的主成分得到了。在下一节，将给出实现算法的代码，来完成一个简单人脸识别的PCA分析。

人脸识别的PCA实现

在Turk的论文里面介绍了PCA在一组人脸识别中的应用，我们将叙述代码及部分关键步骤。
首先数据是一组共四十八张人脸，其中有16个人，每个人有三张在不同光照下的脸，我们称之为矩阵faces，其每一列都是一个人脸向量。
首先计算样本均值

meanFace = mean(faces,2);

再计算协方差矩阵包括其特征值

numFaces = size(faces,2);
meanSub = faces - repmat(meanFace,1,numFaces);
A = meanSub;
[Vp, Dp]=eig(A'*A);

这里面在求特征值的时候，我没有直接计算A*A'而是计算了A'*A，是因为图像向量很长，而样本较少，为了计算方便。得到的A'*A的特征向量，再乘上A矩阵，就是A*A'的特征向量了。
接下来对特征值排序参考上篇文章谱聚类算法及其代码中的eigensort函数，并乘上A矩阵，就得到了我们的特征向量矩阵U

[V,D]=eigsort(Vp,Dp);
U = A*V;

归一化

normU=normc(U);

并且我们计算第五张人脸的主成分

c = normU'* A(:,5);

这样我们就得到了主成分c，使得原本3600维的图像向量，变成了48维的主成分。当然我们在选择特征向量的时候可以只选择前 K 个特征向量，因为其他的影响很少，所以现在我只选择了前10个，并通过主成分重构

numEig = 10;
reducedEig = normU(:,1:numEig);
recon2 = reducedEig * c(1:numEig) + meanFace;
viewcolumn(recon2)

得到的对比结果图5

图5

图5左是原图，图5右是PCA重构后的人脸。可以看到，能够较好的重构原图。

总结

文章从线性空间以及子空间的角度直观分析PCA算法的原理，同时给出了部分数学上的推导，而且叙述了PCA算法的步骤并给出了实际的代码来完成图像识别的应用。PCA算法能够对高纬度的图像进行降维，使得原本需要高纬度，重构的图像依然能够保持较好的原始信息，甚至对原图像有部分优化。

参考文献

• Turk M A, Pentland A P. Face recognition using eigenfaces[C]//Computer Vision and Pattern Recognition, 1991. Proceedings CVPR’91., IEEE Computer Society Conference on. IEEE, 1991: 586-591.
  MLA

• Leon S J. Linear algebra with applications[M]. New York: Macmillan, 1980.

---

1. https://www.cs.ucsb.edu/~mturk/Papers/mturk-CVPR91.pdf ↩
2. https://www.khanacademy.org/math/linear-algebra ↩
3. https://www.cs.ucsb.edu/~mturk/Papers/mturk-CVPR91.pdf ↩