算法导论之图算法

算法导论之图算法

标签（空格分隔）： 学习笔记

---

一、基本图算法

1.1 图的表示

对于图G = （V,E）中，V代表图的顶点，E代表顶点之间的关系，也就是我们通常说的边。按照边的特性我们可以将图分为有向图或者无向图。但是所有的无向图中的边我们可以用两条互指的有向边进行代替，将无向图转换为有向图，所以这里所有的算法都针对有向图。

1.1.1 邻接链表

邻接链表表示方法由一个包含|V|条链表的数组Adj所构成，每个结点有一条链表。对于每个结点 u∈V ，邻接链表Adj[u]包含所有与结点u之间有边链接的结点。下图表示了无向图的邻接链表表示方法。

下图表示了有向图的邻接链表表示方法。采用邻接链表表示法的存储空间需求为 Θ(V+E) 。邻接链表的一个潜在的缺陷是无法快速判断一条边 (u,v) 是否是图中的一条边，唯一的方法是在邻接链表中Adi[u]中遍历搜索结点v。

总结：图的邻接链表存储方式所占空间较少，可用来进行大规模图的存储形式，所占空间为 O(V+E) ;缺点是无法快速判断一条边(u,v)是否是图中的某条边；所以邻接链表通常用来表示稀疏图（顶点较多，边数较少）；

1.1.2 邻接矩阵

对于临街矩阵表示来说，将图表示为一个 |V|∗|V| 的矩阵A = ( aij ),该矩阵满足下述条件：
aij={weight0if (i,j) ∈ E其他


上图的临街矩阵表示如下图所示：

对于无向图来说，图的邻接矩阵存储需占用 O(V22)的空间，有向图需占用 O(V^2) 的存储空间。在图的规模较小的或者是稠密图 （E≥V2） $的情况下，通常使用临近矩阵用来存放图的数据。

---

---

---

---

1.2 图的遍历方式

1.2.1 广度优先遍历

广度优先搜索是最简单的图搜索算法之一，Prim的最小生成树算法和Dijkstra的单源最短路径算法都使用了类似广度优先搜索思想。
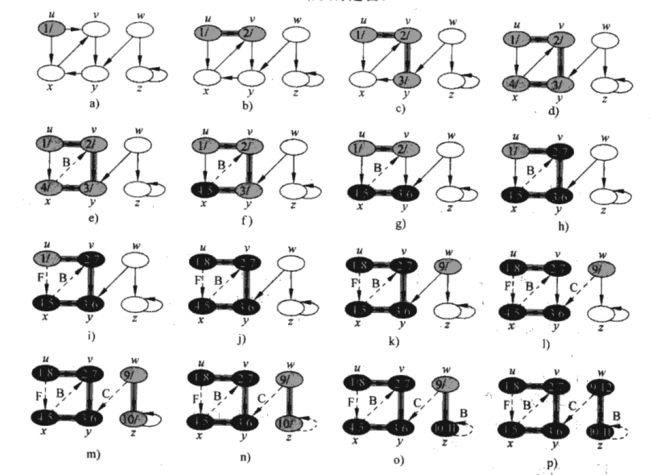
该算法始终将已发现结点和未发现结点之间的边界，沿其广度方向向外扩展，也就是说，算法需要在发现所有距离源结点s为k的所有结点之后，才会发现距离源结点s为k+1的其他结点。为了跟踪算法的进展，广度优先搜索在概念上将每个结点涂上白色，灰色或黑色。所有结点一开始均涂上白色，在第一次遇到一个结点时将此结点涂上灰色，并加入队列，表示已经发现，在搜索了其所有子节点后，将其涂上黑色表示，然后出队。
算法示意图如下图所示：

广度遍历的伪码和C++源码如下

BFS(G, s)                         // 图G=（V,E）使用邻接链表表示
  for each vertex u ∈ G.V - {s}  
      u.color = WHITE             // u结点颜色
      u.d = ∞                    // 从源节点s到u结点的距离
      u.π = NIL                  // u结点在广度优先搜索中的前驱
  s.color = GRAY  
  s.d = 0  
  s.π = NIL  
  Q = Empty  
  ENQUEUE(Q, s)  
  while Q != Empty  
      u = DEQUEUE(Q)  
      for each v ∈ G.Adj[u]  
          if v.color == WHITE  
              v.color = GRAY  
              v.d = u.d + 1  
              v.π = u;  
              ENQUEUE(Q, v)  
      u.color = BLACK 

C++源码

// 广度遍历图
void Graph::bfs(int s)
{
    queue<int> q;
    q.push(s);
    visited[s] = 1;
    while (!q.empty())
    {
        int u = q.front();
        q.pop();
        cout << u << " ";
        GNode *p = edges[u].next;
        while (p != NULL)
        {
            if (!visited[p->val]){    // 未被访问，则将其加入队列中并标志为访问过
                q.push(p->val);
                visited[p->val] = 1;
            }
            p = p->next;
        }
    }

}

void Graph::bfsTravel()
{
    memset(visited, 0, sizeof(int)*vertexNum);
    for (int i = 0; i < vertexNum; i++){
        if (!visited[i])
        {
            bfs(i);
            cout << endl;
        }
    }
}

算法的初始化成本为O(V)，每个结点进行一次入队出队操作，因此队列操作时间为O(V)，扫描邻接链表总时间为O(E)。算法总复杂度为O(V+E)，因此广度搜索时间是图G的邻接链表大小的一个线性函数。

1.2.2 深度优先遍历

深度优先搜索算法总是对最近才发现的结点v的出发边进行探索，直到该结点的所有出发边都被发现为止。一旦结点v的所有边都被发现，搜索则“回溯”到v的前驱结点（v是经过该节点才被发现的），来搜索改前驱结点的出发边。该过程一直持续到从源结点可以达到的所有结点都被发现为止。如果还存在未发现的节点，则深度优先搜索将从这些未发现的结点中任选一个作为一个新的源结点，并重复同样的搜索过程，直到所有结点被发现为止。

深度优先搜索的前驱子图可以形成一个由多棵深度优先树构成的深度优先森林。
在算法中与广度优先搜索相同的是依然用白色、灰色或黑色标记未发现、刚发现、已经搜索完毕的结点。不同的是，深度优先使用两个时间戳来代替源点s到v的距离，第一个时间戳v.d记录结点v第一次被发现的时间（涂上灰色的时候），第二个时间戳v.f记录的是搜索完成对v的邻接链表扫描的时间（涂上黑色的时候），这些时间戳提供了图结构的重要信息，通常能够帮助推断深度优先搜索算法的行为，比如在拓扑排序应用中就起到了重要作用。

算法示意图：

算法伪代码如下所示：

DFS(G)                      //图G=（V,E）使用邻接链表表示
  for each vertex u ∈ G.V  
      u.color = WHITE  
      u.π = NIL  
  time = 0;                 //time是个全局变量，用来计算时间戳
  for each vertex u ∈ G.V  
      if u.color == WHITE  
          DFS-VISIT(G.u)  

DFS-VISIT(G, u)  
  time = time + 1  
  u.d = time  
  u.color = GRAY  
  for each v ∈ G.Adj[u]  
      if v.color == WHITE  
          v.π = u  
          DFS-VISIT(G, v)  
  u.color = BLACK  
  time = time + 1  
  u.f = time 

算法总复杂度为O(V+E)。

1.3 拓扑排序与连通分量

1.3.1 图的拓扑排序

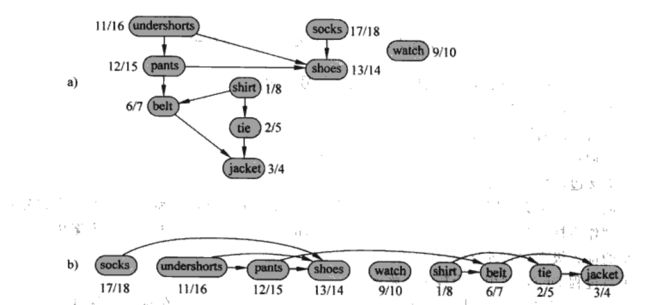
拓扑排序首先需要图G为有向无环图，它是G中所有结点的一种线性次序，该次序满足如下条件：如果图G包含边(u, v)，则结点u在拓扑排序中处于结点v的前面。许多实际应用中都需要使用有向无环图来指明事件的优先次序，拓扑排序可以找出这些进行事件的合理顺序。

拓扑排序算法其实很简单，分为两步：第一步，对有向无环图进行深度优先搜索排序；第二步，将所有结点按照其完成的时间的逆序从左向右排序，此时所有的有向边都是从左指向右。证明神马的具体见算法导论吧。

算法示意图(早上穿衣过程)：

算法伪代码：

TOPOLOGICAL-SORT(G)
  call DFS(G) to compute finishing times v.f for each vertex v
  as each vertex is finished, insert it onto the front of a linked list
  return the linked list of vertices

算法第一步深度优先搜索算法按时间复杂度为O(V+E)，第二步将结点插入链表最前端所需的时间为O(V)，所以总的时间复杂度为O(V+E)。

另外还有一种拓扑排序算法，其思想为首先选择一个无前驱的顶点（即入度为0的顶点，图中至少应有一个这样的顶点，否则肯定存在回路），然后从图中移去该顶点以及由他发出的所有有向边，如果图中还存在无前驱的顶点，则重复上述操作，直到操作无法进行。如果图不为空，说明图中存在回路，无法进行拓扑排序；否则移出的顶点的顺序就是对该图的一个拓扑排序。

算法伪代码：

Topological_Sort_II(G);
  begin  
      for 每个顶点u∈V[G] do d[u]←0;  //初始化d[u],d[u]用来记录顶点u的入度

      for 每个顶点u∈V[G] do
          for 每个顶点v∈Adj[u] 
              do d[v]←d[v]+1;  //统计每个顶点的入度

      CreateStack(s);  //建立一个堆栈s

      for 每个顶点u∈V[G] do  
        if d[u]=0 then push(u,s);  //将度为0的顶点压入堆栈

      count←0; 

      while (not Empty(s)) do
          begin
          u←top(s);  //取出栈顶元素
          pop(s);     //弹出一个栈顶元素
          count←count+1;
          R[count]←u;   //线性表R用来记录拓扑排序的结果

          for 每个顶点v∈Adj[u] do //对于每个和u相邻的节点v
            begin
              d[v]←d[v]-1;
              if d[v]=0 
                  then push(v,s);  //如果出现入度为0的顶点将其压入栈
            end;          
      end;

      if count<>G.size then writeln('Error! The graph has cycle.')
                  else 按次序输出R;
  end;

上面的算法中利用d[u]来记录顶点u的入度，第5-7行用来统计所有顶点的入度，第11-12行将入度为0的顶点压入堆栈，第16-29行不断地从栈顶取出顶点，将该顶点输出到拓扑序列中，并将所有与该顶点相邻的顶点的入度减1，如果某个顶点的入度减至0，则压入堆栈，重复该过程直到堆栈空了为止。显而易见该算法的复杂度为O(VE)，因为第5-7行的复杂性就是O(VE)，后面16-29行的复杂性也是O(VE)。这个算法虽然简单，但是没有前面一个算法的效率高。