0030算法笔记——【回溯法】最大团问题和图的m着色问题

     1、最大团问题

     问题描述

     给定无向图G=(V, E)，其中V是非空集合，称为顶点集；E是V中元素构成的无序二元组的集合，称为边集，无向图中的边均是顶点的无序对，无序对常用圆括号“( )”表示。如果U∈V，且对任意两个顶点u，v∈U有(u, v)∈E，则称U是G的完全子图(完全图G就是指图G的每个顶点之间都有连边)。G的完全子图U是G的团当且仅当U不包含在G的更大的完全子图中。G的最大团是指G中所含顶点数最多的团。

     如果U∈V且对任意u，v∈U有(u, v)不属于E，则称U是G的空子图。G的空子图U是G的独立集当且仅当U不包含在G的更大的空子图中。G的最大独立集是G中所含顶点数最多的独立集。

     对于任一无向图G=(V, E)，其补图G'=(V', E')定义为：V'=V，且(u, v)∈E'当且仅当(u, v)∈E。
     如果U是G的完全子图，则它也是G'的空子图，反之亦然。因此，G的团与G'的独立集之间存在一一对应的关系。特殊地，U是G的最大团当且仅当U是G'的最大独立集。

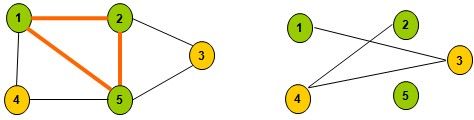
     例：如图所示，给定无向图G={V, E}，其中V={1,2,3,4,5}，E={(1,2), (1,4), (1,5),(2,3), (2,5), (3,5), (4,5)}。根据最大团(MCP)定义，子集{1,2}是图G的一个大小为2的完全子图，但不是一个团，因为它包含于G的更大的完全子图{1,2,5}之中。{1,2,5}是G的一个最大团。{1,4,5}和{2,3,5}也是G的最大团。右侧图是无向图G的补图G'。根据最大独立集定义，{2,4}是G的一个空子图，同时也是G的一个最大独立集。虽然{1,2}也是G'的空子图，但它不是G'的独立集，因为它包含在G'的空子图{1,2,5}中。{1,2,5}是G'的最大独立集。{1,4,5}和{2,3,5}也是G'的最大独立集。

     算法设计

     无向图G的最大团和最大独立集问题都可以用回溯法在O(n2^n)的时间内解决。图G的最大团和最大独立集问题都可以看做是图G的顶点集V的子集选取问题。因此可以用子集树来表示问题的解空间。首先设最大团为一个空团，往其中加入一个顶点，然后依次考虑每个顶点，查看该顶点加入团之后仍然构成一个团，如果可以，考虑将该顶点加入团或者舍弃两种情况，如果不行，直接舍弃，然后递归判断下一顶点。对于无连接或者直接舍弃两种情况，在递归前，可采用剪枝策略来避免无效搜索。为了判断当前顶点加入团之后是否仍是一个团，只需要考虑该顶点和团中顶点是否都有连接。程序中采用了一个比较简单的剪枝策略，即如果剩余未考虑的顶点数加上团中顶点数不大于当前解的顶点数，可停止继续深度搜索，否则继续深度递归当搜索到一个叶结点时，即可停止搜索，此时更新最优解和最优值。

     算法具体实现如下：

//最大团问题 回溯法求解
#include "stdafx.h"
#include 
#include 
using namespace std;

const int N = 5;//图G的顶点数
ifstream fin("5d7.txt");   

class Clique
{
	friend int MaxClique(int **,int[],int);
	private:
		void Backtrack(int i);
		int **a,		//图G的邻接矩阵
			n,			//图G的顶点数
			*x,			//当前解
			*bestx,		//当前最优解
			cn,			//当前顶点数
			bestn;		//当前最大顶点数
};

int MaxClique(int **a, int v[], int n);

int main()
{
	int v[N+1];
	int **a = new int *[N+1];  
    for(int i=1;i<=N;i++)    
    {    
        a[i] = new int[N+1];    
    } 
	
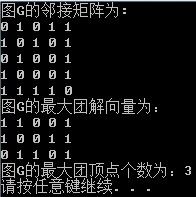
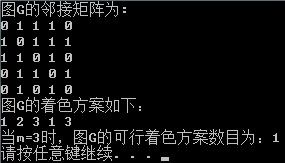
	cout<<"图G的邻接矩阵为:"<>a[i][j];      
            cout< n) // 到达叶结点
	{
		for (int j = 1; j <= n; j++)
		{
			bestx[j] = x[j];
			cout<= bestn)// 进入右子树
	{
		x[i] = 0;
		Backtrack(i+1);
	}
}

int MaxClique(int **a, int v[], int n)
{
	Clique Y;

	//初始化Y
	Y.x = new int[n+1];
	Y.a = a;
	Y.n = n;
	Y.cn = 0;
	Y.bestn = 0;
	Y.bestx = v;
	Y.Backtrack(1);
	delete[] Y.x;
	return Y.bestn;
}

     程序运行结果如图：

     2、图的m着色问题

     问题描述

       给定无向连通图G和m种不同的颜色。用这些颜色为图G的各顶点着色，每个顶点着一种颜色。是否有一种着色法使G中每条边的2个顶点着不同颜色。这个问题是图的m可着色判定问题。若一个图最少需要m种颜色才能使图中每条边连接的2个顶点着不同颜色，则称这个数m为该图的色数。求一个图的色数m的问题称为图的m可着色优化问题。

     四色猜想：四色问题是m图着色问题的一个特例，根据四色原理，证明平面或球面上的任何地图的所有区域都至多可用四种、颜色来着色，并使任何两个有一段公共边界的相邻区域没有相同的颜色。这个问题可转换成对一平面图的４－着色判定问题(平面图是一个能画于平面上而边无任何交叉的图)。将地图的每个区域变成一个结点，若两个区域相邻，则相应的结点用一条边连接起来。多年来，虽然已证明用5种颜色足以对任一幅地图着色，但是一直找不到一定要求多于4种颜色的地图。直到1976年这个问题才由爱普尔，黑肯和考西利用电子计算机的帮助得以解决。他们证明了4种颜色足以对任何地图着色。

     算法设计

     考虑所有的图，讨论在至多使用m种颜色的情况下，可对一给定的图着色的所有不同方法。通过回溯的方法，不断的为每一个节点着色，在前面n-1个节点都合法的着色之后，开始对第n个节点进行着色，这时候枚举可用的m个颜色，通过和第n个节点相邻的节点的颜色，来判断这个颜色是否合法，如果找到那么一种颜色使得第n个节点能够着色，那么说明m种颜色的方案是可行的。

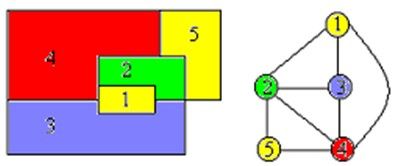
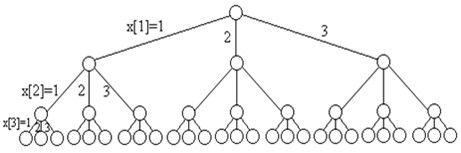
     用m种颜色为无向图G=(V,E)着色，其中，V的顶点个数为n，可以用一个n元组x=(x1,x2,…,xn)来描述图的一种可能着色，其中，xi∈{1, 2, …, m}，(1≤i≤n)表示赋予顶点i的颜色。例如，5元组(1, 2, 2, 3, 1)表示对具有5个顶点的无向图（a）的一种着色，顶点A着颜色1，顶点B着颜色2，顶点C着颜色2，如此等等。如果在n元组X中，所有相邻顶点都不会着相同颜色，就称此n元组为可行解，否则为无效解。容易看出，每个顶点可着颜色有m种选择，n个顶点就有mn种不同的着色方案，问题的解空间是一棵高度为n的完全m叉树，这里树高度的定义为从根节点到叶子节点的路径的长度。每个分支结点，都有m个儿子结点。最底层有mn个叶子结点。例如，表示用3种颜色为3个顶点的图着色的状态空间树。如图所示，对第i（i>=1）层上的每个顶点，从其父节点到该节点的边上的标号表示顶点i着色的颜色编号。

    算法具体实现代码如下：

//图的着色问题 回溯法求解
#include "stdafx.h"
#include 
#include 
using namespace std;

const int N = 5;//图的顶点数
const int M = 3;//色彩数
ifstream fin("5d8.txt"); 

class Color
{
	friend int mColoring(int, int, int **);
	private:
		bool Ok(int k);
		void Backtrack(int t);
		int n,		//图的顶点数
			m,		//可用的颜色数
			**a,	//图的邻接矩阵
			*x;		//当前解
		long sum;	//当前已找到的可m着色方案数
};

int mColoring(int n,int m,int **a);

int main()
{
	int **a = new int *[N+1];  
    for(int i=1;i<=N;i++)    
    {    
        a[i] = new int[N+1];    
    } 
	
	cout<<"图G的邻接矩阵为:"<>a[i][j];      
            cout<n)
	{
		sum++;
		for (int i=1; i<=n; i++)
		cout << x[i] << " ";
		cout << endl;
	}
    else
	{
		for (int i=1;i<=m;i++) {
			x[t]=i;
			if (Ok(t)) Backtrack(t+1);
		}
	}
}

bool Color::Ok(int k)// 检查颜色可用性
{
	for (int j=1;j<=n;j++)
	{
		if ((a[k][j]==1)&&(x[j]==x[k])) //相邻且颜色相同
		{
			return false;
		}
	}
	return true;
}

int mColoring(int n,int m,int **a)
{
	Color X;

	//初始化X
	X.n = n;
	X.m = m;
	X.a = a;
	X.sum = 0;
	int *p = new int[n+1];
	for(int i=0; i<=n; i++)
	{
		p[i] = 0;
	}
	X.x = p;
	X.Backtrack(1);
	delete []p;
	return X.sum;
}

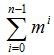     图m可着色问题的解空间树中内结点个数是。对于每一个内结点，在最坏情况下，用ok检查当前扩展结点的每一个儿子所相应的颜色可用性需耗时O(mn)。因此，回溯法总的时间耗费是。程序运行结果如图：