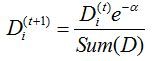机器学习算法6-AdaBoost元算法
本文来自
一. 什么是元算法(meta-algorithm)
元算法就是对其他算法进行组合的一种方式。也称为集成算法(ensemble method),例如bagging方法和boosting
方法。它可以是不同算法的集成;也可以是同一算法在不同设置下的集成;还可以是数据集不同部分分配给不同分类
器之后的集成。
二. boosting方法与bagging方法的区别
bagging方法:也称为自举汇聚法(bootstrap aggregating)。是从原始数据集中选择S次后得到S个新数据集的一
种技术。这S个数据集的大小和原始数据集的大小一样。每个数据集都是在原始数据集上随机选择S次并替换得到的。
因此,新的数据集可能有重复的样本,原始数据集中的某些样本也可能不在新的数据集中。S个数据集经训练最后会
得到S个分类器,应用这S个分类器对测试样本进行分类,得到S个结果,选择投票结果中最多的类别作为最后的分类
结果。
boosting方法:与bagging方法很类似,说使用的多个分类器的类型是一样的。bagging方法中,不同的分类器是
通过串行训练得到的,每个分类器都根据已训练出的分类器的性能来进行训练。boosting是通过集中关注被已有分类
器错分的那些数据来获得新的分类器。
另外,boosting分类结果是基于所有分类器的加权求和结果的,而bagging方法中的分类器权重是相等的,
boosting方法的权重并不相等,每个权重代表的是其对应分类器在上一轮迭代中的成功度。boosting方法有很多版
本,AdaBoost是其中一个比较优秀的版本。
三. AdaBoosting算法(Adaptive boosting)
自适应boosting,对训练数据中的每一个样本赋予一个权重,这些权重构成了向量D。一开始,这些权重值被初
始化为相等值。首先,在训练数据上训练出一个弱分类器并计算该分类器的错误率,然后在同一数据集上再次训练弱
分类器。在第二次训练分类器时,将会重新调整每个样本的权重,其中第一次分对的样本的权重将会降低,而第一次
分错的样本权重将会提高。为了从所有的弱分类器中得到最终的分类结果,AdaBoost为每个分类器都分配了一个权重
值为alpha,这些alpha值是基于每个弱分类器的错误率进行计算的。其中,错误率为:
r = 未正确分类的样本数目 / 所有样本数目
而alpha的计算公式为:
计算出alpha值后,可以对权重向量D进行更新,更新规则为:
样本被正确分类,那么权重值更改为:
样本未被正确分类,那么权重值更改为:
AdaBoosting会不断重复训练和调整上述权重的过程,直至训练错误率为0或者弱分类器的数目达到用户指定值为止。
四.非均衡分类
监督学习中,使用错误率(测试样本中错分的样例比例)来衡量分类器任务的成功程度,往往掩盖了样例如何被
错分的事实。而通常的分类问题上,往往存在非均衡分类,即做出某种决策导致的代价并不一样。因此,我们还可以
采用以下指标来衡量分类器的性能。
1.混淆矩阵(confusion matrix)可以帮助人们更好地了解分类中的错误,而错误率往往掩盖了样例如何被错分的
事实。
2.几个概念:
若一个正例被判为正例,则认为产生了一个真正例(True Positive, TP, 也成真阳);如果一个反例正
确地被判为反例,则认为产生了一个真反例(True Negative, TN, 也成为真阴);另外两个分别被称为伪反例(False
Negative, 也成为假阴),和伪正例(False Positive, FP, 也成为假阳)。
因此,在分类中,当某个类别的重要性高于其他类别时,我们可以利用上述定义来定义出多个比错误率更好的新
指标。(1)正确率(Precision):它等于TP/(TP+FP),给出的是预测为正例的样本中的真正正例的比例。(2)召回率
(Recall),它等于TP/(TP+FN),给出的是预测为正例的真实正例占所有真实正例的比例。
3.ROC曲线(ROC curve):
ROC曲线代表接受者操作特征(receiver operating characteristic)。其横轴伪正例的比例(FP/(FP+TN))。
而纵轴是真正例的比例(TP/(TP+FN))。ROC曲线给出的是当 阈值变化时假阳例和真阴率的变化情况。对不同ROC曲
线进行比较的一个指标是曲线下的面积(Area Under the Curse:AUC)。AUC给出的分类器的平均性能值,当然并不能
完全代替整条曲线的观察。一个完美分类器的AUC为1.0,而随机才测的AUC为0.5。
4.代价敏感的学习(cost-sensitive learning)
即给出做出任意决策的代价表,通过计算总代价最小来选择分类器类型。
在分类算法中,很多可以引入代价信息。在AdaBoost中,可以基于代价函数来调整错误权重向量D。在朴素贝叶
斯中,可以选择具有最小期望代价而不是最大概率的类别作为最后的结果。在SVM中,可以在代价函数中对于不同的
类别选择不同的参数C。
5.过抽样(unsersampling)与欠抽样(oversampling)
为了针对非均衡问题来调节分类器,可以对分类器的训练数据进行改造。因此,可以通过欠抽样和过抽样实现。
过抽样意味复制样例,而欠抽样意味着删除样例。通常的一种策略就是使用反例类别的欠抽样与正例类别的过抽样
相结合的方法。
另外,要对正例样例进行过抽样,我们可以复制已有样例或者加入与已知样例相似的点。一种是加入已有数据点
的插值点,但是这种做法会导致过拟合问题。
五. 总结
本章介绍了boosting方法中最为流行的一个称为AdaBoosting的算法。AdaBoosting以弱学习器作为基础分类器,
并且输入数据,使其通过权重向量进行加权。在第一次迭代当中,所有数据都等权重。但是在后续的迭代中,前次迭
代中分错的数据的权重会增大。这种针对错误的调节能力正是AdaBoost的长处。
以单层决策树作为弱学习器构建了AdaBoost分类器。实际上,AdaBoosting函数可以应用于任意分类器,只要该
分类器能够处理加权数据即可。AdaBoost算法十分强大,它能够快速处理其他分类器很难处理的数据集。