CornerNet: Detecting Objects as Paired Keypoints论文详解
《CornerNet: Detecting Objects as Paired Keypoints》发表于ECCV2018
代码地址:https://github.com/princeton-vl/CornerNet
文章认为采用anchor进行目标检测的方式有两个不好的地方:第一,为了确保anchor能够尽可能的覆盖的所有的标注框,往往需要大量的anchor,而其中只有少部分是真正有效的,这样会导致训练时正负样本的不平衡和减慢训练速度;第二,anchor的方式需要引入各种超参数,比如anchor大小、比例、数量等。因此文章提出一种新的目标检测方式,不使用anchor来进行目标检测。文章使用左上角点和右下角点来表示检测框,所以文章提出的网络通过预测框的左上角点,右下角点和角点的嵌入向量(embedding vector)来得到最终的检测框。
下面来详细说明文章的原理
一、网络结构
网络结构如下图所示,可以看出文章采用的是16年用于姿态识别的网络hourglass作为主干网络。该主干网络提取出来的特征输入到两个模块中,一个模块用来预测左上角点,另一个用来预测右下角点。每个预测角点的模块都有自己的corner pooling,最终输出有角点对应的热图(heatmaps)、嵌入向量(embeddings)和角点的偏移信息。
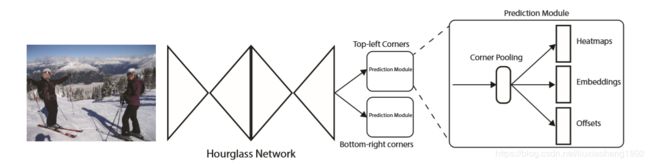
1.1 hourglass网络
文章使用的网络由文章《Stacked hourglass networks for human pose estimation》提出,用来做人体姿态识别的任务。该网络是全卷积网络,由一个或者多个hourglass模块组成。一个hourglass模块先用一系列的卷积和maxpooling层对输入进行特征提取,同时提取出的特征会有下采样的效果,然后通过一系列的上采样和卷积操作使得特征图又慢慢变大。通过这些操作hourglass模块能将图片的局部信息和全局信息提取出来。通过多个hourglass的堆叠,网络可以更好的获取到一些高维信息,使得网络很适合用于物体检测的任务。因为特征图的先小后大,很像沙漏,网络因此而得名。
文章用了两个hourglass模块堆叠而成,且相对于原始的hourglass模块,文章做了一些小的修改。首先,文章用stride为2的卷积代替maxpooling操作。对输入的分辨率下采样5次,每次输出的特征通道数为(256,384,384,384,512)。在上采样的过程中应用了最近邻上采样接2个残差模块的方式(代码好像并没有,只是简单的上采样,然后和之前的卷积结果相加)。在与上采样相加之前之前的卷积结果会进过两个残差模块。在hourglass模块的中间,也就是512通道处有4个残差模块。输入hourglass之前,图片会进过一个 7 × 7 7\times7 7×7stride为2的卷积和一个stride为2的残差模块。
同《Stacked hourglass networks for human pose estimation》类似,在两个hourglass模块的连接处,使用了内部监督(intermediate supervision),即将第一个模块的输入经过 1 × 1 1\times1 1×1Conv-BN和第一个模块的输出也经过 1 × 1 1\times1 1×1Conv-BN的结果相加后送给ReLU,得到的结果在经过一个残差模块送入第二个hourglass模块。这里大致的结构如下图所示,详细的实现请参考代码。
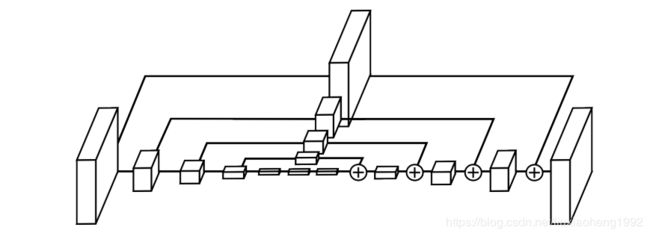
1.2角点检测
网络预测的角点输出是左上角点和右下角点的return结果。每种热图有C个通道(C为预测的类别数),热图大小和图片一样大为 H × W H\times W H×W。输出的每个通道都是二值的mask图像,用来表示每个像素是否为角点。
对于每一个角点来说,只有一个点是正样本,其他都是负样本,但由于某些错误的点对得到的框仍能和真实的标注框有很高的重叠。所以在训练时靠近正样本的负样本有一定惩罚权重,即越靠近正样本的负样本受到的越小。惩罚权重是通过未归一化2D高斯分布( e − x 2 + y 2 2 σ 2 e^{-\frac{x^2+y^2}{2\sigma^2}} e−2σ2x2+y2)来赋值的。待减少惩罚的负样本,也就是上面所说的正样本附近的负样本(附近的定义就是负样本的位置使得得到的框与groundtruth的IOU小于0.3的点),且这些点是以正样本为中心一定半径内的点,如下图所示。而高斯分布中的 σ \sigma σ就是半径的1/3。

因为在全卷积的网络中,往往会有卷积的featuremap的大小比原图小的情况,因此对于原图中坐标为(x,y)的点,对应到featuremap中的坐标为 ( ⌊ x n ⌋ , ⌊ y n ⌋ ) (\lfloor \frac{x}{n} \rfloor, \lfloor \frac{y}{n} \rfloor) (⌊nx⌋,⌊ny⌋),其中n为下采样的因子。当我们将特征图上的点还原到原图时会导致精度的损失。为了解决这个问题网络还会预测还原至原图需要的偏移量。偏移量的gt计算如下所示:
o k = ( x k n − ⌊ x k n ⌋ , y k n − ⌊ y k n ⌋ ) o_{k}=\left(\frac{x_k}{n}-\lfloor\frac{x_k}{n}\rfloor, \frac{y_k}{n}-\lfloor\frac{y_k}{n}\rfloor\right) ok=(nxk−⌊nxk⌋,nyk−⌊nyk⌋)
上式中, o k o_{k} ok表示偏移量, ( x k , y k ) (x_k,y_k) (xk,yk)表示原图的坐标点。
1.3 角点配对(grouping corners)
这部分原文写了几段,包括的loss是怎么计算的,先不管loss的计算,先要弄懂文中写的embedding是什么。
更广义的来说,用来进行角点配对的embedding指的是网络输出的featuremap,这个featuremap大小与预测角点的featuremap大小一样。在对应角点的位置处的feature就认为是这个角点的embedding,文章用的embedding是1维的,也就是说一个角点对应一个预测值,当预测的左上角点和右下角点的embedding值很小时,认为这两个预测点是属于同一个框的。
1.4 Corner Pooling
这个是文章为了更好的预测角点位置提出的一个新的pooling方法。拿左上角点来说,为了更好的判断featuremap中的某一点是左上角点,它需要以它当前的位置向右水平扫视,和向下竖直扫视来得到一个值(可以认为是左上角点的响应值)。对于一张大小为 H × W H\times W H×W的特征图,对于特征图上的点(i,j),corner pooling的计算方式为:
t i , j = { m a x ( f t i , j , t ( i + 1 ) j ) i f i < H f t H j o t h e r w i s e t_{i,j}=\left\{ \begin{array}{lr} max(f_{t_{i,j}}, t_{(i+1)j}) \quad if \quad i <H \\ f_{t_{Hj}} \quad otherwise \end{array} \right. ti,j={max(fti,j,t(i+1)j)ifi<HftHjotherwise
l i , j = { m a x ( f t i , j , l i ( j + 1 ) ) i f j < W f l i W o t h e r w i s e l_{i,j}=\left\{ \begin{array}{lr} max(f_{t_{i,j}}, l_{i(j+1)}) \quad if \quad j <W \\ f_{l_{iW}} \quad otherwise \end{array} \right. li,j={max(fti,j,li(j+1))ifj<WfliWotherwise
右下角点同理,提取到的两个方向的最大值后相加就是pooling的最终结果。这种pooling方法能够采用动态规划的方式高效的计算,如下图所示
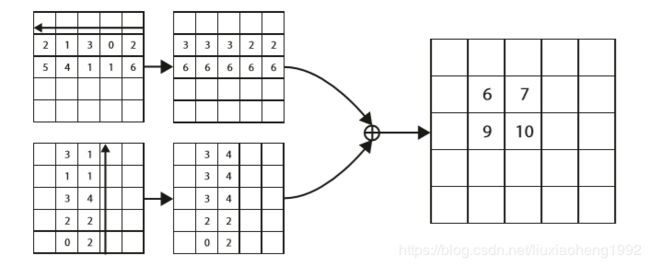
pooling的最终结果会参与到角点的位置估计、角点的偏移量估计、角点的embedding计算中去,如下图所示
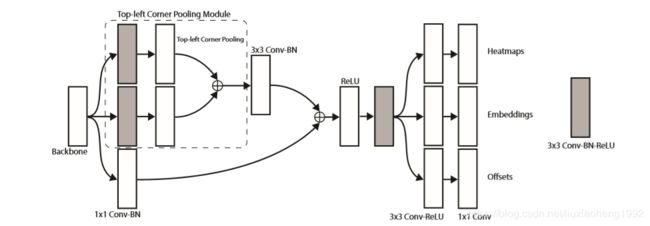
二、 loss的计算
本文有几种loss,一个是角点估计的loss,一个是角点偏移位置估计的loss,一个是角点组合估计的loss。下面来单个说明一下。
2.1 角点位置估计的loss计算
角点位置估计的loss计算,该loss是focal loss的变式:
L d e t = − 1 N ∑ c = 1 C ∑ = 1 H ∑ j = 1 W { ( 1 − p c i j ) α l o g ( p c i j ) i f y c i j = 1 ( 1 − y c i j ) β ( p c i j ) α l o g ( 1 − p c i j ) o t h e r w i s e L_{det}=\frac{-1}{N}\sum^{C}_{c=1}\sum^{H}_{=1}\sum^{W}_{j=1}\left\{ \begin{array}{lr} (1-p_{c_{ij}})^{\alpha}log(p_{c_{ij}}) \quad if y_{c_ij}=1 \\ (1-y_{c_{ij}})^{\beta}(p_{c_{ij}})^{\alpha}log(1-p_{c_{ij}}) \quad otherwise\end{array} \right. Ldet=N−1∑c=1C∑=1H∑j=1W{(1−pcij)αlog(pcij)ifycij=1(1−ycij)β(pcij)αlog(1−pcij)otherwise
上式中,N是一张图片中物体的个数, α \alpha α和 β \beta β是两个超参数这里分别取为2和4。 p c i j p_{c_{ij}} pcij是在预测map中对于c类物体在坐标(i,j)下的概率值,对应位置的gt为 y c i j y_{c_{ij}} ycij,这里注意的是 y c i j y_{c_{ij}} ycij是根据高斯分布和标定真值求出来用于训练的值, ( 1 − y c i j ) (1-y_{c_{ij}}) (1−ycij)用来作为真值附近的负样本的惩罚项。
2.2 角点位置偏移的loss计算
上面说到由于卷积下采样的操作会产生一定的偏移现象,偏移量用 o k o_{k} ok表示,偏移量的loss计算采用smooth L1 loss表示:
L o f f = 1 N ∑ k = 1 N S m o o t h L 1 L o s s ( o k , o ^ k ) L_{off}=\frac{1}{N}\sum^{N}_{k=1}SmoothL1Loss(o_{k},\hat{o}_k) Loff=N1∑k=1NSmoothL1Loss(ok,o^k)
其中 o k o_{k} ok表示真值的偏移, o ^ k \hat{o}_{k} o^k表示预测的偏移量。
2.3 角点组合估计的loss
上面提到了角点组合预测用的是embedding值的距离,而embedding值本文用的是1维的,可以认为网络对于每个预测点输出的embedding值是一个值,对于k类物体来说左上角点的embedding值用 e t k e_{t_k} etk表示,对于右下角用 e b k e_{b_k} ebk表示,loss计算如下:
L p u l l = 1 N ∑ k = 1 N [ ( e t k − e k ) 2 + ( e b k − e k ) 2 ] L_{pull}=\frac{1}{N}\sum^{N}_{k=1}\left[(e_{t_k}-e_{k})^2+(e_{b_k}-e_k)^2\right] Lpull=N1∑k=1N[(etk−ek)2+(ebk−ek)2]
L p u s h = 1 N ( N − 1 ) ∑ k = 1 N ∑ j = 1 , j ≠ k N m a x ( 0 , δ − ∣ e k − e j ∣ ) L_{push}=\frac{1}{N(N-1)}\sum^N_{k=1}\sum^{N}_{j=1,j\neq k} max(0,\delta-|e_k-e_j|) Lpush=N(N−1)1∑k=1N∑j=1,j̸=kNmax(0,δ−∣ek−ej∣)
其中 e k e_k ek表示 e t k e_{t_k} etk和 e b k e_{b_k} ebk的均值, δ \delta δ本文设置为1.这里一个叫pull loss为了将两个一组的点对中每个点对平均值距离越近,从而loss更小。一个叫push loss,为了将不是一组的点对距离更远从而loss越小
根据上面各个loss,文中总的loss计算为:
L = L d e t + α L p u l l + β L p u s h + γ L o f f L=L_{det}+\alpha L_{pull}+\beta L_{push} + \gamma L_{off} L=Ldet+αLpull+βLpush+γLoff
文中, α \alpha α和 β \beta β都设为0.1, γ \gamma γ设为1。
到这里文章原理基本介绍完了,对于一些实验的结果和分析详情可以查看原文。
欢迎加入Object Detection交流,群聊号码:910457072