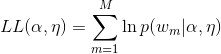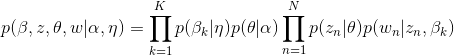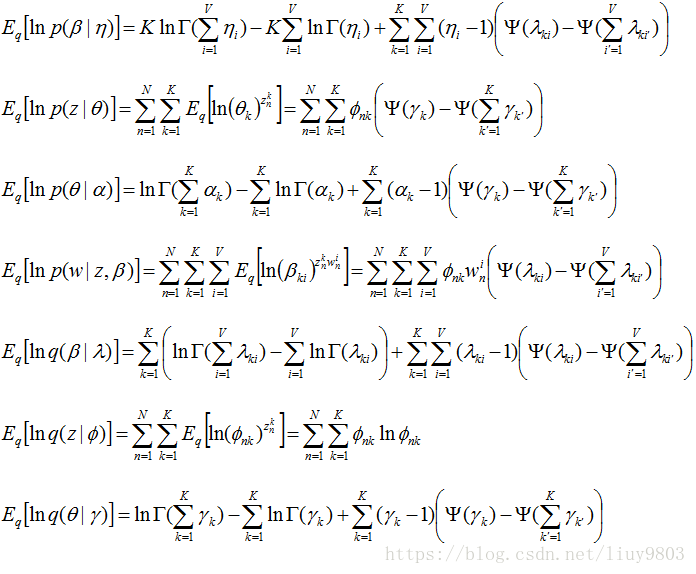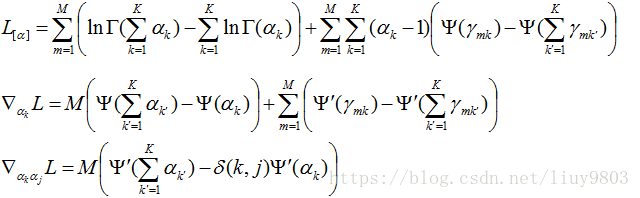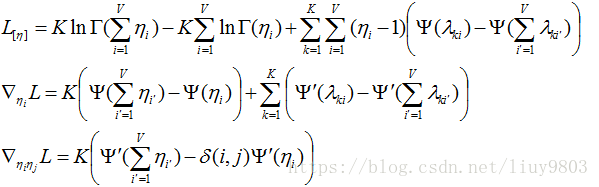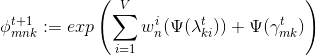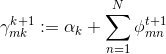机器学习主题模型之LDA参数求解——变分推断+EM近似
由上一篇可知LDA主要有两个任务：对现有文集确定LDA模型参数α、η的值；或对一篇新文档，根据模型确定隐变量的分布p(β,z,θ|w,α,η)。由于无法直接求出这个后验分布，因此可以考虑使用Laplace近似、变分近似、MCMC、Gibbs采样法等算法求解。
1、变分推断（variational inference）
我们希望找到合适的α、η使对似然函数最大化，并求出隐变量的条件概率分布：
w表示一篇文档中所有N个单词，每个单词都有唯一对应的主题，
为K维向量，当且仅当文档中第n个词的主题为k时，
；否则
。
V表示词典大小，当且仅当文档中第n个词是词典中第i个词时，
；否则
。
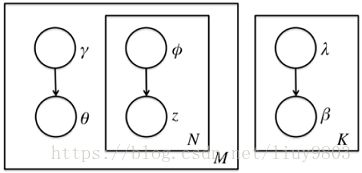
但由于隐变量θ、β之间存在耦合关系，使用EM算法时E步无法直接求解它们基于条件概率分布的期望，因此使用变分法引入mean field assumption，假设所有的隐变量都是通过各自独立的分布生成的，即去掉隐变量之间的连线和w结点，并赋予β、z、θ各自独立分布，λ、Φ、γ为变分参数。
可得隐变量β、z、θ的联合分布q为：
为了让变分分布q(β,z,θ|λ,Φ,γ)能够近似地表示真实后验p(β,z,θ|w,ɑ,η)，则让二者的KL散度D(q||p)尽可能小：
![D(q||p)=\sum_{x}^{ }q(x)ln\frac{q(x)}{p(x)}=E_{q(x)}[\ln q(x)-\ln p(x)]](http://img.e-com-net.com/image/info8/75dafc29d9a643b3927fc503ad46dc66.gif){kind=small}
文档数据的对数似然可以写为（省略q中的变分参数λ,Φ,γ为了书写简便）：
由Jensen不等式可以得到对数似然的下界，上式左右两部分的差是变化的后验概率与真实后验概率之间的KL散度，令L(λ,Φ,γ;ɑ,η)表示对数似然的下界，称L为Evidence Lower BOund（ELBO），有：
为了让D(q||p)尽可能小，又对数似然函数不影响KL散度，则应该让L尽可能大。将L根据贝叶斯展开可得：
第一项展开为：
2、指数分布族的性质
对第三项的求解，需要引入指数分布族的性质。指数分布族是指分布函数满足如下形式的概率分布：
T(x)是分布的充分统计量（sufficient statistic）。对于给定的统计推断问题，包含了原样本中关于该问题的全部有用信息的统计量；对于未知参数的估计问题，保留了原始样本中关于未知参数的全部信息的统计量，就是充分统计量（不损失信息）。
η是自然参数（natural parameter）；
A(θ)是对数配分函数（partition function），即归一化因子的对数形式，使得概率分布的积分为1。
指数分布族包含了很多常见分布，如正态分布、伯努利分布、泊松分布、beta分布、Γ分布、Dirichlet分布等，它们的均值和方差都有简洁的表达式。指数分布族的性质有：
（1）指数分布族是唯一的充分统计量是有限大小的分布族；
（2）指数分布族是唯一存在共轭先验的分布族；
（3）指数分布族是选定限制下作的假设最少的分布族；
（4）指数分布族是广义线性模型的核心内容；
（5）指数分布族是变分推断的核心内容。
3、极大化ELBO求解变分参数
由指数分布族的性质可知![E_{q}[\ln p(\beta |\eta )]](http://img.e-com-net.com/image/info8/ff3b815a4e1540109e18cc4fff13c03b.gif){kind=small}
第三项可写为：
其中
因此L的所有7个子项展开分别为：
以上7个式子相加得到L后，使用EM算法求解变分参数和模型参数：
E步关于λ,Φ,γ极大化L得到真实后验分布的近似分布q；
M步固定变分参数ɑ,η极大化L，反复迭代直到收敛。
4、EM算法E步求解变分参数
通过对L的各个变分参数λ,Φ,γ分别求导并令偏导等于0，可以得到迭代表达式，多次迭代收敛后即为最佳变分参数。
（1）只考虑L含有Φ的部分，根据限制条件
构造Lagrange函数并令L对Φ的偏导=0可得：
注意其中的当且仅当文档中第n个词为词典中的第i个词，因此上式中的第一项的求和只计算了一项。
（2）只考虑L含有γ的部分，并令L对γ的偏导=0可得：
（3）只考虑L含有λ的部分，并令L对γ的偏导=0可得：
参数λ决定了β分布，对于整个训练文集是共有的，因此参数λ实际应按照如下方式更新：
E步的过程就是循环计算
、
、
直到收敛。
5、EM算法M步更新模型参数
M步固定变分参数，极大化ELBO得到最优模型参数。求解最优的模型参数ɑ、η方法有很多，如梯度下降法、牛顿法等，LDA一般使用牛顿法，即通过求L关于ɑ、η的一阶导数和二阶导数的表达式，迭代求解ɑ、η在M步的最优解。
（1）基于整个文集M篇文档只考虑L含有ɑ的部分，并求L对ɑ求二阶导为：
其中当且仅当k=j时，δ(k,j)=1，否则δ(k,j)=0。
（2）类似ɑ的处理过程，只考虑L含有η的部分，并求L对η求二阶导为：
其中当且仅当k=j时，δ(k,j)=1，否则δ(k,j)=0。
6、LDA变分推断EM算法流程总结
输入：主题总数K、文集D，D中含有M个文档与相应的词典V。
initialize 
and 
for all k and i
while not converged do:
// E-step
initialize 
for all m,n,k
initialize 
for all m,k
initialize 
for all k,i
repeat
for m=1 to M:
for n=1 to 
:
for k=1 to K:
normalize 
to sum to 1
for k=1 to K:
for i=1 to V:
until convergence
// M-step
update α and η using Newton-Raphson method with the newly estimated variational parameters fixed.
参考资料
Blei 03 LDA implementation
https://blog.csdn.net/u011414416/article/details/51168242
http://www.cnblogs.com/pinard/p/6873703.html