Dijkstra算法、Floyd算法的区别与联系，并由此谈到greedy和DP

首先，Dijkstra算法与Floyd算法都是广度优先搜索的算法。都可以用来求单源点到其他所有点的最短路径。那么这两者的原理分别是怎样?彼此又有什么区别呢？

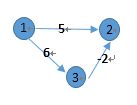
求此有向图中起点1到其他所有点的最短距离

在本文中，我们以一个小小的包含3个节点的有向图和邻接矩阵Graph来进行说明。

Graph[3][3] = {0,5,6
                1000,0,1000
                1000,-2,0}

Dijskra算法

采用Dijkstra算法，需要有一个源点集合u，一个参考点集合v，以及一个滚动dist数组，用于存储S点到达其他所有点的最短路径。
如果需要记录最短路线，还需要配置一个pre数组，用来存储当前最短路径下Index序号的点的前驱节点。
初始化时，u中只有源点s，其他点都在v中，dist数组是s到其他所有点的直接距离，若没有边连接则为无穷大（本例中1000表示无穷大）。

初始化状态：u={1},v={2,3},dist[]={0,5,6},pre[]={1,1,1},flag={0,1,1}

算法开始，遍历dist查找最小值，将该最小值对应的点添加到u中，并从v中删除。一种实现方式是采用flag数组,0表示在u中，1表示在v中。

中间状态1：u={1,2},v={3},dist[]={0,5,6},pre[]={1,1,1},flag={0,0,1}

接着需要更新dist数组，判断从起始点1到v中的点之间的路径上插入新加入的点2，路径是否能变得更短，也就是比较dist[j]和Graph[1][2]+dist[2]，然后使用较小值更新dist[j]，若dist[j]被更新，则将pre[j]修改为2.

中间状态2：u={1,2},v={3},dist[]={0,5,6},pre[]={1,1,1},flag={0,0,1}

然后循环上述步骤，判断在v中且dist最小的点，然后加入到u中。

中间状态3: u={1,2,3},v={},dist[]={0,5,6},pre[]={1,1,1},flag={0,0,0}

此时发现v中已没有点，则结果被输出。

很显然，这个结果是不对的，从1到2的最短路径应该是1->3->2，长度为4. 而不是1->2，长度为5

这是因为按照Dijkstra的算法逻辑，是不能计算负权图的。
Dijkstra算法本质上是贪心算法，下一条路径都是由当前更短的路径派生出来的更长的路径。不存在回溯的过程。
如果权值存在负数，那么被派生出来的可能是更短的路径，这就需要过程可以回溯，之前的路径需要被更短的路径替换掉，而Dijkstra算法是不能回溯的。它每一步都是以当前最优选择为前提的。

Floyd算法

那么，Floyd算法会怎么做呢？Floyd算法实际上是一个动态规划算法。
每一个点对u和v之间的最短路径，可能会经过N个点，这些中间点记为k。
假定u到k之间的最短路径已经找好，k到v之间的最短路径已经找好，那么求u到v之间的最短路径，就是遍历各个可能的k点，然后求(u,k)+(k,v)之间的最小值。
所以这实际上将大规模的问题自顶向下划分为了小规模的问题，这就是动态规划思想。

那么算法的步骤是怎样的呢？
需要使用三层循环：

for(u){
       for(v){
               for(k)}}

若graph[u][k]+graph[k][v] < graph[u][v],则更新graph[u][v]。并记录以当前u为起点的情况下此点的前驱。
当三层遍历完毕之后，所有点对之间的最短路径长度和路径就能求出来了。当然，如果只需要求某个点到其他所有点的最短距离，那么固定u，也就是说只用两层遍历就可以做到了。
最后的矩阵为

{0,4,6
1000,0,1000
998,-2,0}

可以看到，求得的最短路径及其长度均是正确的。
这是因为动态规划是可以回溯的，会遍历到从1到3再从3到2的路径。

总结

上述算法均为两种经典算法的最简单形式，没有任何优化。比如Floyd可以从空间复杂度上进行优化，Dijkstra在选择v中dist最小值时可以使用堆排序等。

本文意在引出一个关于贪心算法和动态规划算法之间区别与联系的论述。（出自邹博老师）
考虑一阶马尔科夫模型，状态N仅仅可以从状态N-1得到，就像有限状态自动机，这就是正确使用贪心算法的前提。
考虑高阶马尔科夫模型，状态N可能需要前面的状态N-1,N-2,N-3等等一起联合才能得到。这就是正确使用动态规划的前提。
所以一定能用贪心算法解的问题肯定可以由动态规划解。但是可以用动态规划来解的问题，不一定能用贪心算法来解。

使用马尔科夫模型来类比动态规划思想的这个观点还有很多启发思维的地方。
比如说在构建状态转移方程时，经常因为使用的状态不对，而列不出最终的状态转移方程。
简单的状态转移方程，只需要考虑一个状态x的变化，而复杂的状态转移方程可能需要考虑x、y或者更多的状态迁移。那么如何找准这些影响最终结果的状态，并找准状态和结果之间的对应关系，是列好状态转移方程的一个重点。