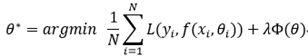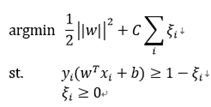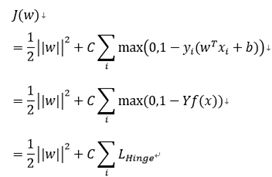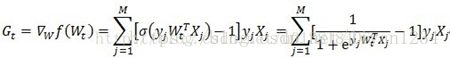机器学习(五)——常见损失函数
笔者是一个痴迷于挖掘数据中的价值的学习人,希望在平日的工作学习中,挖掘数据的价值,找寻数据的秘密,笔者认为,数据的价值不仅仅只体现在企业中,个人也可以体会到数据的魅力,用技术力量探索行为密码,让大数据助跑每一个人,欢迎直筒们关注我的公众号,大家一起讨论数据中的那些有趣的事情。
我的公众号为:livandata
1) 损失函数有哪几种:
通常机器学习每一个算法中都会有一个目标函数,算法的求解过程是通过对这个目标函数优化的过程。在分类或者回归问题中,通常使用损失函数(代价函数)作为其目标函数。损失函数用来评价模型的预测值和真实值不一样的程度,损失函数越好,通常模型的性能越好。不同的算法使用的损失函数不一样。
损失函数分为经验风险损失函数和结构风险损失函数。经验风险损失函数指预测结果和实际结果的差别,结构风险损失函数是指经验风险损失函数加上正则项。通常表示为如下:
其中,前面的均值项表示经验风险函数,L表示损失函数,后面的是正则化项(regularizer)或惩罚项(penalty term),它可以是L1、L2或者其他正则函数。整个式子表示要找到使得目标函数最小的值。
下面介绍几种常见的损失函数:
0-1损失函数和绝对值损失函数:
0-1损失是指,预测值和目标值不相等为1,否则为0:
感知机就是用的这种损失函数。但是由于相等这个条件太过严格,因此我们可以放宽条件,即满足时认为相等。
绝对值损失函数:
![]()
log对数损失函数:
Logistic回归的损失函数就是对数损失函数,在Logistic回归的推导中,它假设样本服从伯努利分布(0-1)分布,然后求得满足该分布的似然函数,接着用对数求极值。Logistic回归并没有求对数似然函数的最大值,而是把极大化当做一个思想,进而推导它的风险函数为最小化的负的似然函数。从损失函数的角度上,它就成为了log损失函数。
log损失函数的标准形式:
![]()
在极大似然估计中,通常都是先取对数再求导,再找极值点,这样做是方便计算极大似然估计。损失函数L(Y,P(Y|X))是指样本X在标签Y的情况下,使概率P(Y|X)达到最大值(利用已知的样本分布,找到最大概率导致这种分布的参数值)。
平方损失函数:
最小二乘法是线性回归的一种方法,它将回归的问题转化为了凸优化的问题。最小二乘法的基本原则是:最优拟合曲线应该使得所有点到回归直线的距离和最小。通常用欧式距离进行距离的度量。平方损失的损失函数为:
指数损失函数:
AdaBoost就是一指数损失函数为损失函数的。
指数损失函数的标准形式:
![]()
Hinge损失函数:
Hinge loss用于最大间隔(maximum-margin)分类,其中最有代表性的就是支持向量机SVM。
Hinge函数的标准形式:
![]()
(与上面统一的形式:![]() )
)
其中,t为目标值(-1或+1),y是分类器输出的预测值,并不直接是类标签。其含义为,当t和y的符号相同时(表示y预测正确)并且|y|≥1时,hinge loss为0;当t和y的符号相反时,hinge loss随着y的增大线性增大。
在支持向量机中,最初的SVM优化的函数如下:
将约束项进行变形,则为:
则损失函数可以进一步写为:
因此,SVM的损失函数可以看做是L2正则化与Hinge loss之和。
几种损失函数的曲线如下图:
2) 如何并行化(并行算法的几种优化方法)?
1.1 ModelAssessmentwith Cross validation
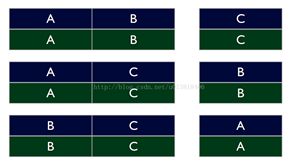
相信对机器学习比较熟的都经常用交叉验证,简单解释一下就是把样本划分为n块相同大小的,选一些出来做训练集,剩下的做验证集,比较常见的是就留1块数据集做验证集。如果留1块数据集做验证的话,也就是说我们需要训练n个模型,用图说明一下:
这里将数据分成ABC三块,分别使用AB,AC,BC作为训练集,用C,B,A作为验证集,在这个实验中我们需要生成3个模型,然而这3个模型的生成时是可以并行的或者分布式的,将AB在node1上生成模型,AC和BC在node2和node3上生成模型,各自拉下来每个结点需要训练的数据就可以开始并行或者分布式跑模型.
1.2 ModelSelectionwith Grid Search
对于确定的机器学习算法选择参数也是一个比较大的工程,拿SVM打比方,一般SVM需要设置核函数、gamma和惩罚系数C,假如每个参数有三种选择,那么我们需要跑3*3*3=27个模型才能确定参数设置。现在假设有两个参数param_1有3个设置1,10,100,param_2有三个设置1e3,1e4,1e5,再结合交叉验证现在如图所示
1.3 BaggingModels:Random Forests
Bagging models是集成算法,按比例抽取样本集得到新的样本集合,然后根据多个新样本集合训练出不同的模型,以随机森林为例子,随机森林的bag稍微有点不同,它不仅仅随机抽取样本,还随机抽取属性,抽取完后,每个样本集合生成一个树模型,对于回归问题就求树的均值,对于分类问题就按vote数目,这种并行也非常好理解,我直接上一段sklearn的代码:
[python] view plain copy
1. trees = Parallel(n_jobs=self.n_jobs, verbose=self.verbose, backend="threading")(
2. delayed(_parallel_build_trees)(
3. t, self, X, y, sample_weight, i, len(trees),
4. verbose=self.verbose, class_weight=self.class_weight)
5. for i, t in enumerate(trees))
这里需要了解一下joblib里面Parallel(我在joblib里面还看到了一个parallel函数说明差不多)和delayed用法,delayed获取后面函数的参数并分发给前面的n_jobs,Parallel建立多进程或者多线程通过backend选择,mulprocessing(多进程)threading(多线程),其实python还有一个Parallel的包不止支持多核还支持局域网内多台机器.
1.4 In-LoopAveragedModels
前面讲到的所有的方法都是将模型作为一个最小单位来进行并行或者分布式的,也就是说并没有模型内的参数共享的考虑,比较直观的就是tensorflow的多cpu或gpu同步随机梯度下降,使用tensorflow建立模型后计算每个可训练变量的更新参数,然后对不同设备计算出来的结果进行取均值更新。举两个算法例子,用LR和决策树打比方
LR并行化:
假设用随机梯度下降来更新参数,计算梯度公式如下
可以看出这个计算可以并行化的地方主要是矩阵的乘法与加法,其实也就是用分布式的矩阵乘法来优化,想要详细过程的可以查看这个博客
决策树的并行化:
对数据集进行横切与纵切得到这样的
ps.本来想看下sklearn svm的并行的,发现是直接调用的libsvm就没看了,还有就是sklearn LR用的是二分的,如果出现多个标签,也就是ONE VS REST,sklearn会先调整损失函数,然后使用parallel来训练n(n-1)/2个分类器.
1.5、MapReduce实现并行化处理:
MapReduce本身为并行化架构,所有的逻辑必须放在Map和reduce的两个方法中,输入和输出必须是一个个的任务,任务之间没有通讯,唯一可以交互处理的地方在于shuffle中,在机器学习的算法中,EM算法可以直接在mapreduce中应用,E步在map中操作,M步在reduce中操作,可以时间迭代的操作建模;